Có bao nhiêu giá trị nguyên của m để đồ thị hàm số $y=mx+\frac{1}{x}$  có hai điểm cực trị và tất cả các điểm cực trị đều thuộc hình tròn tâm O, bán kính 6?

Cho đồ thị hàm số $\left(C\right):y=x^4-2\left(m^2+1\right)x^2+m^4$ . Gọi A,B  , C là ba điểm cực trị của $\left(C\right)$  và $S_1$ , $S_2$  lần lượt là phần diện tích phía trên và phía dưới trục hoành của tam giác ABC. Có bao nhiêu giá trị của tham số  sao cho $\frac{S_1}{S_2}=\frac{1}{3}$ ?

Có bao nhiêu giá trị thực của tham số m để hàm số$y=\frac{1}{3}{x}^3-x^2+\left(m^2-3\right)x$  có hai điểm cực trị  $x_1,x_2$sao cho giá trị biểu thức $P=\left|x_1\left(x_2-2\right)-2\left(x_2+1\right)\right|$  đạt giá trị lớn nhất?

Giả sử A, B là hai điểm cực trị của đồ thị hàm số $y=x^3+a{x}^2+bx+c$ và đường thẳng (AB) đi qua gốc tọa độ. Giá trị lớn nhất $P_{\min }$  của $P=abc+ab+c$  bằng

Cho hàm số$y=2x^3-3m{x}^2+x+m$ . Gọi S là tập hợp các giá trị nguyên của tham số m trong khoảng$\left(-10;10\right)$ để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của đường thẳng$y=x-6$ . Số phần tử của tập S là

Có bao nhiêu giá trị nguyên của $m\in \left[-20;20\right]$  để hàm số $y=\frac{1}{3}{x}^3-m{x}^2+mx-1$  có hai điểm cực trị  $x_1$, $x_2$  sao cho $\left|x_1-x_2\right|\ge 2\sqrt{6}$ ?

Có bao nhiêu giá trị nguyên của $m\in \left[-18;18\right]$ để đồ thị hàm số$y=\left(x-1\right)\left(x^2+2mx+1\right)$ có hai điểm cực trị nằm về hai phía trục hoành?

Các điểm cực đại của hàm số $f\left(x\right)=x-2\sin x$  có dạng (với $k\in \mathbb{Z}$ )

Tìm m để đồ thị hàm số $y=(x-1)(x^2+2mx+1)$  có hai điểm cực trị nằm cùng phía với trục hoành.

Giá trị của m để đồ thị hàm số $y=\frac{m}{3}{x}^3+\left(m-1\right)x^2+\left(m+2\right)x-6$ có hai điểm cực trị có hoành độ dương là

Cho hàm số $y=x^3-3m{x}^2+4m^2-2$ có đồ thị (C) và điểm $C\left(1;4\right)$ . Tổng các giá trị nguyên dương của m để (C) có hai điểm cực trị A, B sao cho tam giác ABC có diện tích bằng 4 là

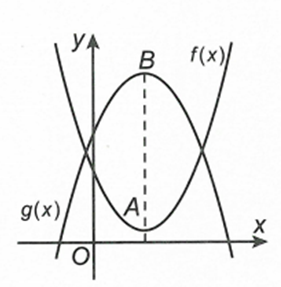
Cho hai hàm đa thức $y=f\left(x\right)$ , $y=g\left(x\right)$ có đồ thị là hai đường cong như hình vẽ. Biết rằng đồ thị hàm số $y=f\left(x\right)$  có đúng một điểm cực trị là , đồ thị hàm số $y=g\left(x\right)$  có đúng một điểm cực trị là (với $x_A=x_B$ ) và $AB=\frac{7}{2}$ . Có bao nhiêu giá trị nguyên của$m\in \left(-10;10\right)$ để hàm số $y=\left|\left|f\left(x\right)-g\left(x\right)\right|+m\right|$  có đúng bảy điểm cực trị?