Cho tứ diện ABCD trong đó AB ⊥ AC, AB ⊥ BD. Gọi P và Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ vuông góc với nhau.
 Giải bởi Vietjack
Giải bởi Vietjack
Cộng từng vế (1) và (2) ta có:
Phương pháp chứng minh 2 đường thẳng vuông góc
Để chứng minh hai đường thẳng vuông góc với nhau ta có thể làm theo các cách sau:
+ Gọi u→ và v→ là hai vecto chỉ phương của hai đường thẳng; chứng minh: u→. v→ = 0
⇒ (u→ ; v→) = 90°
+ Dùng định lí Pytago đảo chứng minh hai đường thẳng vuông góc.
+ Nếu a // a’; b // b’ và a ⊥ b thì a' ⊥ b'
Bài tập liên quan:
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
Cách giải:
Ta cần chứng minh
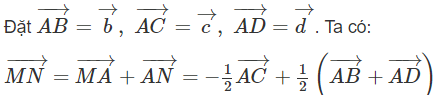
Theo giả thiết ta có:
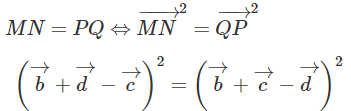
Tham khảo thêm một số tài liệu liên quan:
Phương pháp giải và bài tập về Cách chứng minh hai đường thẳng vuông góc
Cho hình hộp thoi ABCD.A'B'C'D' có tất cả các cạnh bằng a và . Chứng minh tứ giác A'B'CD là hình vuông.
Cho hình chóp A.ABC có SA = SB = SC = AB = AC = a và BC = a√2. Tính góc giữa hai đường thẳng AB và SC.
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau (hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B'D'
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và . Tính góc giữa hai vectơ .
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thằng song song thì vuông góc với đường thẳng kia.