A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
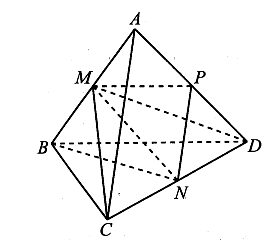
Gọi M, N, P lần lượt là trung điểm của các cạnh AB, CD, AD.
Ta có .
Theo công thức tính đường trung tuyến ta có
.
Tương tự nên:
Áp dụng định lí Cô-sin cho tam giác PMN ta có:
.
Vậy .
Cho x, y ( ) là hai số thực dương thỏa mãn . Giá trị của biểu thức là
Cho hàm số có bảng biến thiên như sau.
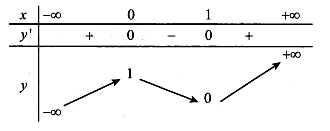
Tìm m để phương trình có bốn nghiệm phân biệt .
Trong một lớp học có 35 học sinh. Muốn chọn ra một lớp trưởng, một lớp phó thì số cách chọn là
Cho hàm số . Biết hàm số có hai điểm cực trị là x=1 ,x=2 và f(0)=1 . Giá trị của biểu thức là
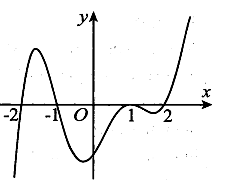
Cho hàm số y=f(x) là hàm đa thức bậc 5 có đồ thị hàm số y=f'(x) như hình vẽ. Hàm số y=f(x) đồng biến trên những khoảng nào trong các khoảng sau đây?
Cho thỏa mãn . Biết phương trình có nghiệm duy nhất . Giá trị của biểu thức là
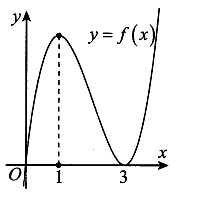
Cho hàm số y=f(x) có đồ thị như hình vẽ. Tất cả giá trị của tham số m để đồ thị hàm số có đúng 3 điểm cực trị là
Tại sân ga, có một đoàn tàu gồm 8 toa. Có 5 hành khách lên tàu, độc lập với nhau, mỗi người lên 1 toa ngẫu nhiên. Xác suất để sau khi hành khách lên tàu, đoàn tàu còn 7 toa trống là
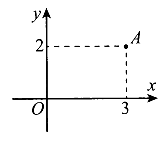
Điểm A trong hình vẽ bên biểu diễn cho số phức z. Tìm phần thực và phần ảo của số phức .
Cho tam giác ABC đều cạnh a. Gọi (P) là mặt phẳng chứa BC và vuông góc với (ABC) . Trong (P) xét đường tròn (C) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C) và đỉnh A bằng
Một chiếc cốc có dạng hình trụ, chiều cao là 16cm, đường kính đáy bằng 8cm, bề dày thành cốc và đáy cốc là 1cm. Nếu đổ một lượng nước vào cốc cách miệng cốc 5cm thì ta được khối nước có thể tích , nếu đổ đầy cốc ta được khối trụ (tính cả thành cốc và đáy cốc) có thể tích . Tỉ số bằng
Cho hàm số có bảng biến thiên như hình vẽ sau.
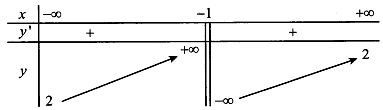
Mệnh đề nào sau đây đúng?