Cho tập hợp L = {n| n = 2k + 1 với k ∈ N}.
a) Nêu bốn số tự nhiên thuộc tập L và hai số tự nhiên không thuộc tập L;
b) Hãy mô tả tập L bằng cách nêu dấu hiệu đặc trưng theo một cách khác.
Giải bởi Vietjack
L = {n| n = 2k + 1 với k ∈ N }.
a)
+) Với k = 0, ta được: n = 2. 0 + 1 = 1 ∈ L
+) Với k = 1, ta được: n = 2. 1 + 1 = 3 ∈ L
+) Với k = 2, ta được: n = 2. 2 + 1 = 5 ∈ L
+) Với k = 3, ta được: n = 2. 3 + 1 = 7 ∈ L
Do đó bốn số tự nhiên thuộc tập L là: 1; 3; 5; 7
Vậy ta thấy hai số tự nhiên không thuộc tập L là: 0; 2
b)
Nhận thấy các số: 1; 3; 5; 7; ... là các số tự nhiên lẻ.
Tương tự với mọi số tự nhiên k thì ta tìm được các số n thuộc tập hợp L đều là các số tự nhiên lẻ.
Do đó ta viết có thể viết tập hợp L bằng cách nêu dấu hiệu đặc trưng khác như sau:
L = {n ∈ ℕ | n là các số lẻ}.
Bài tập liên quan:
Cho tập hợp P =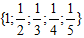 
. Hãy mô tả tập hợp P bằng cách nêu dấu hiệu đặc trưng của các phần tử của nó.
Cách giải:
Nhận xét:
+) Các phần tử trên giống nhau đều có tử bằng 1 vì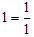 
+) Các phần tử có mẫu số là các số tự nhiên lớn hơn 0 và nhỏ hơn 6 (hoặc nhỏ hơn hoặc bằng 5)
Do đó em có thể viết tập hợp M bằng một trong các cách sau:
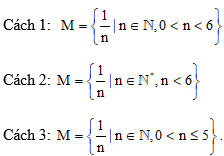
Tham khảo thêm một số tài liệu liên quan:
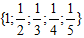. Hãy mô tả tập hợp P bằng cách nêu dấu hiệu đặc trưng của các phần tử của nó.CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
