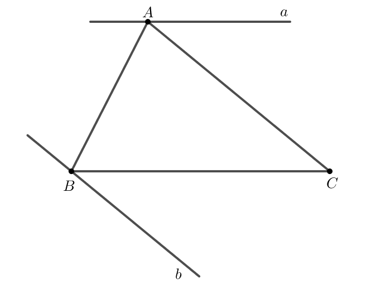
Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
 Giải bởi Vietjack
Giải bởi Vietjack
Theo tiên đề Euclid, chỉ vẽ được duy nhất một đường thẳng a, một đường thẳng b.
Qua điểm A nằm ngoài đoạn BC, vẽ được duy nhất một đường thẳng song song với BC. Do đó ta chỉ có thể vẽ được 1 đường thẳng a.
Qua điểm B nằm ngoài đoạn AC, vẽ được duy nhất một đường thẳng song song với AC. Do đó ta chỉ có thể vẽ được 1 đường thẳng b.
Tiên đề Euclid được phát biểu: “Qua một điểm M nằm ngoài đường thẳng a ...”
A. có duy nhất một đường thẳng đi qua M và song song với a.
B. có hai đường thẳng song song với a.
C. có ít nhất một đường thẳng song song với a.
D. có vô số đường thẳng song song với a.
Quan sát hình vẽ bên. Biết m // n.
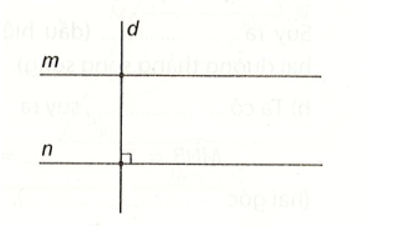
Khẳng định nào sau đây đúng?
A. d // m;
B. d // n;
C. d ⊥ m;
D. m ⊥ n.
Số đo góc HAB trong hình bên là:
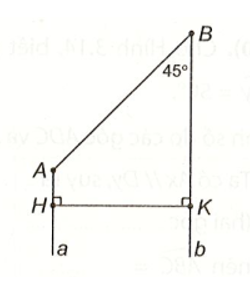
A. 45°;
B. 90°;
C. 180°;
D. 135°.
Cho Hình 3.14, biết rằng Ax // Dy, Tính số đo các góc ADC và ABC.