Cho tam giác ABC có DE // BC (Hình 55).
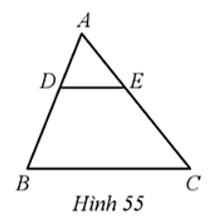
Khẳng định nào dưới đây đúng?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Tam giác ABC có DE // BC nên theo hệ quả của định lí Thalès ta có:
Suy ra
Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau tại H. Chứng minh:
a) ∆EBH ᔕ ∆DCH, ∆ADE ᔕ ∆ABC;
b) DB là tia phân giác của góc EDI, với I là giao điểm của AH và BC.
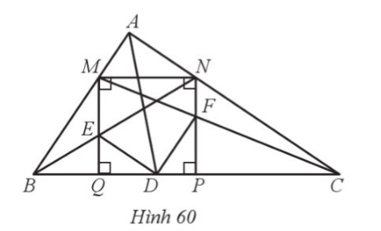
Cho tam giác ABC vuông tại A, có đường phân giác AD. Vẽ hình vuông MNPQ ở đó M thuộc cạnh AB, N thuộc cạnh AC, P và Q thuộc cạnh BC. Gọi E và F lần lượt là giao điểm của BN và MQ, CM và NP (Hình 60). Chứng minh:
a) DE song song với AC;
b) DE = DF.
Cho hình bình hành ABCD (AC > BD). Vẽ CE vuông góc với đường thẳng AB tại E, CF vuông góc với đường thẳng AD tại F, BH vuông góc với đường thẳng AC tại H. Chứng minh:
a) ∆ABH ᔕ ∆ACE; ∆CBH ᔕ ∆ACF.
b) BH2 = HK.HQ, biết tia BH cắt dường thẳng CD tại Q; cắt cạnh AD tại K.
Cho tam giác ABC có ba góc nhọn, điểm I thuộc cạnh BC và IM, IN lần lượt là đường phân giác của các góc AIC và AIB. Chứng minh: AN.BI.CM = BN.IC.AM.
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MC = 2MB. Đường thẳng qua M song song với AC cắt AB ở D. Đường thẳng qua M song song với AB cắt AC ở E. Gọi x, y lần lượt là chu vi tam giác DBM và tam giác ECM. Tính x + 2y, biết chu vi tam giác ABC bằng 30 cm.
∆ABC ᔕ ∆DEF theo tỉ số đồng dạng k, ∆MNP ᔕ ∆DEF theo tỉ số đồng dạng q. Khi đó, ∆ABC ᔕ ∆MNP theo tỉ số đồng dạng là:
A. k + q.
B. kq.
C.
D.
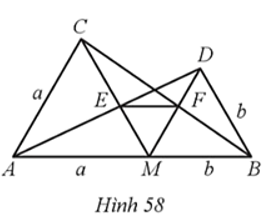
Cho điểm M thuộc đoạn thẳng AB, với MA = a, MB = b. Vẽ hai tam giác đều AMC và BMD; gọi E là giao điểm của AD và CM, F là giao điểm của DM và BC (Hình 58).
a) Chứng minh EF // AB.
b) Tính ME, MF theo a, b.
Cho ∆MNP ᔕ ∆M’N’P’ và Số đo góc P là:
A. 30°.
B. 40°.
C. 70°.
D. 110°.
Cho tam giác ABC. Các điểm M, N lần lượt thuộc các cạnh AB và AC thỏa mãn MN // BC và Tỉ số bằng
A.
B.
C.
D.
Cho hình thang ABCD, AB // CD, Tính diện tích tam giác BDC, biết diện tích tam giác ABD là 44,8 cm2.
Hình 54 cho biết A’B’ = 4, A’O = 3, AO = 6, OB = x, AB = y.
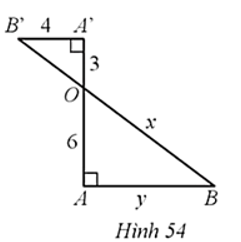
Giá trị của biểu thức x + y là:
A. 22.
B. 18.
C. 20.
D. 16.
Cho tam giác ABC cân tại A, AB = 10 cm, BC = 12 cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Tính độ dài AI.
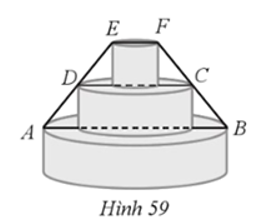
Một chiếc kệ bảy hoa quả có ba tầng được thiết kế như Hình 59. Tầng đáy có đường kính AB là 32 cm. Tầng giữa có đường kính CD nhỏ hơn đường kính tầng đáy là 12 cm. Tính độ dài đường kính tầng trên cùng EF, biết EF // AB; D, C lần lượt là trung điểm của EA và FB.
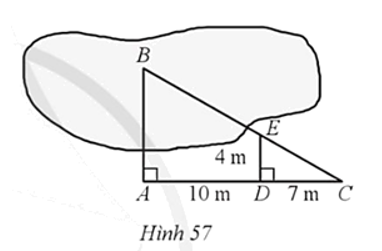
Để đo khoảng cách AB, trong đó điểm B không tới được, người ta tiến hành đo bằng cách lấy các điểm C, D, E sao cho AD = 10 m, CD = 7 m, DE = 4 m (Hình 57). Khi đó, khoảng cách AB (tính theo đơn vị mét và làm tròn kết quả đến hàng phần mười) là:
A. 9,3 m.
B. 9,4 m.
C. 9,6 m.
D. 9,7 m.