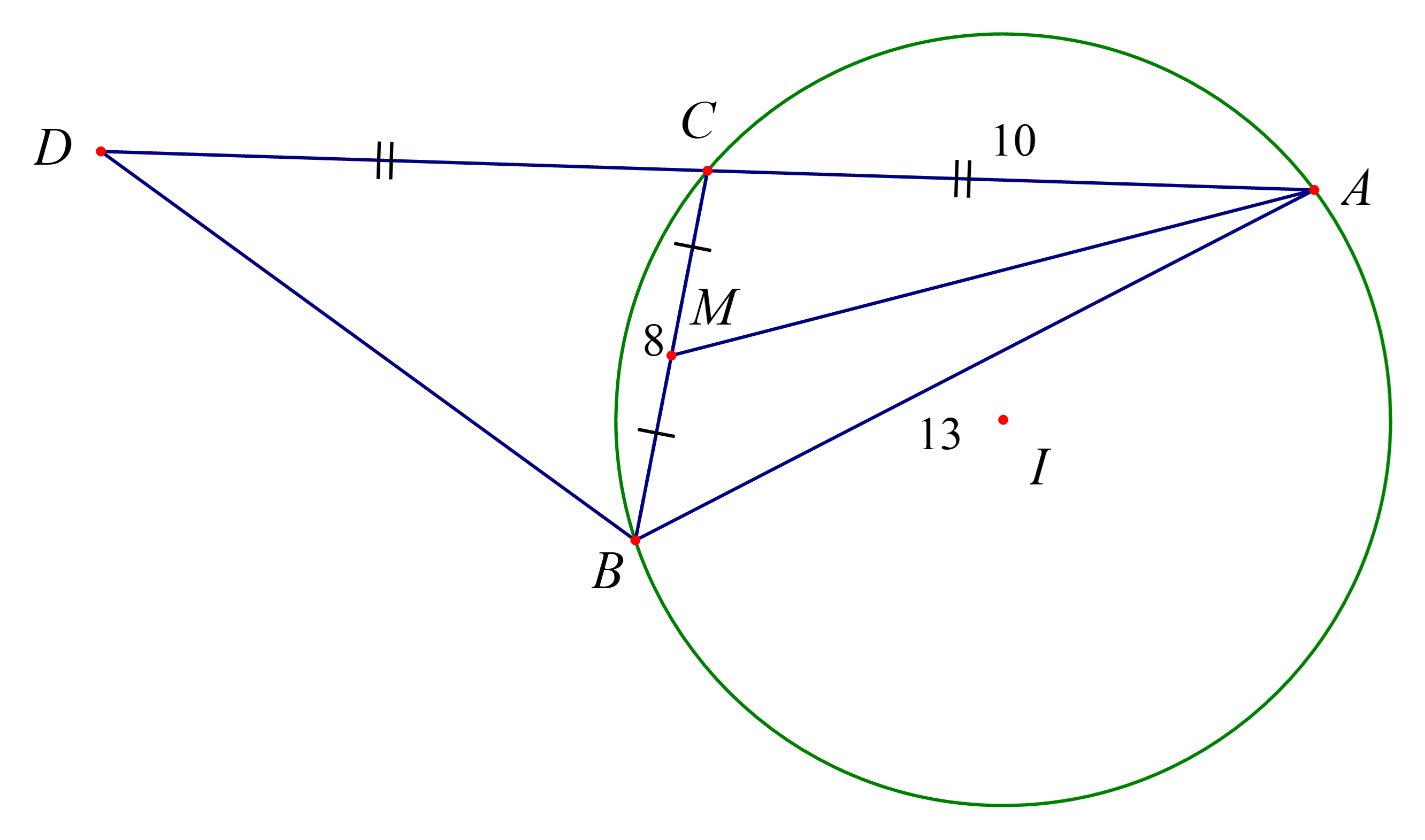
Cho tam giác ABC có a = 8, b = 10, c = 13.
a) Tam giác ABC có góc tù không?
b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.
c) Lấy điểm D đối xứng với A qua C. Tính độ dài BD.
Giải bởi Vietjack
a) Áp dụng hệ quả của định lí côsin ta có:
cosC =
⇒
Suy ra
Vậy tam giác ABC là tam giác tù.
b) Do AM là đường trung tuyến nên M là trung điểm của BC, tức là MB = MC = BC : 2 = 4.
Áp dụng định lí côsin cho tam giác ACM ta có:
AM2 = AC2 + CM2 – 2.AC.CM.cosC = 102 + 42 – 2.10.4.cos91°47'26" = 118,5
⇒ AM ≈ 10,9.
Nửa chu vi của tam giác ABC là :
Áp dụng công thức Heron ta có diện tích tam giác ABC là:
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó ta có:
Vậy độ dài đường trung tuyến AM ≈ 10,9; diện tích tam giác ABC là 40; bán kính đường tròn ngoại tiếp tam giác ABC là 6,5.
c) Vì D đối xứng với A qua C nên C là trung điểm của AD.
Suy ra AD = 2AC = 2.10 = 20.
Áp dụng hệ quả của định lí côsin cho tam giác ABC ta có:
cosA =
Áp dụng định lí côsin cho tam giác ABD ta có:
BD2 = AD2 + AB2 – 2.AD.AB.cosA = 202 + 132 – 2.20.13. = 159
⇒ BD = ≈ 12,6.
Vậy BD ≈ 12,6.
Cho tam giác ABC có , b = 8, c = 5. Tính:
a) Cạnh a và các góc , ;
b) Diện tích tam giác ABC;
c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Cho hình bình hành ABCD.
a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.
b) Cho AB = 4, BC = 5, BD = 7. Tính AC.
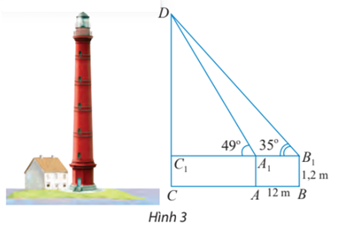
Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2 m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được . Tính chiều cao CD của tháp.
Cho tam giác ABC. Biết a = 49,4; b = 26,4; . Tính hai góc và cạnh c.
Cho tam giác ABC có a = 15, b = 20, c = 25.
a) Tính diện tích tam giác ABC.
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.
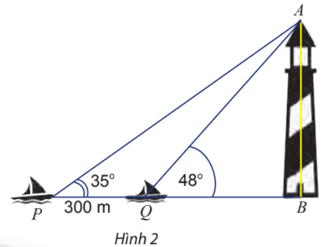
Hai chiếc tàu thủy P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc và . Tính chiều cao của tháp hải đăng đó.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
