Cho hình vuông ABCD cạnh a. Tính
A.-1
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Từ giả thiết suy ra
Ta có
Chọn C
Định nghĩa
Cho hai vectơ 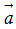
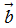
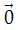
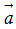
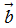
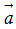
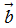
Trường hợp ít nhất một trong hai vectơ 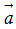
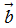
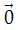
Chú ý
+) Với 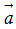
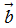
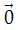
+) Khi 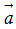
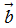
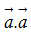
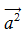
Ta có:
Xem thêm một số kiến thức liên quan:
Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1; -1) và B(3; 0). Tìm tọa độ điểm D, biết D có tung độ âm.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 4;1); B(2; 4); C(2; -2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách từ đó đến điểm N(- 1; 4) bằng
Trong mặt phẳng tọa độ Oxy, cho hai vectơ và Tìm tọa độ vectơ biết và
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 3) và B(4; 2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(6; 0); B(3;1) và C(-1; -1). Tính số đo góc B của tam giác đã cho.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(-2; 2) và N(1; 1).Tìm tọa độ điểm P thuộc trục hoành sao cho ba điểm M; N; P thẳng hàng.
Trong mặt phẳng tọa độ Oxy, cho hai vectơ và . Tìm vectơ biết và .
Trong mặt phẳng tọa độ Oxy, cho hai vectơ và Tìm m để vectơ tạo với vectơ một góc 450.