Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
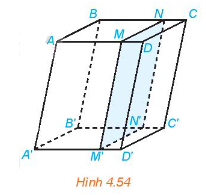
Hình hộp ABCD.A'B'C'D' có hai đáy ABCD và A'B'C'D' là các hình bình hành.
Ta có: AD // BC (do ABCD là hình bình hành), do đó AD // (BCC'B').
Lại có: AA' // BB' (các cạnh bên của hình hộp), do đó AA' // (BCC'B').
Mặt phẳng (ADD'A') chứa hai đường thẳng cắt nhau AD và AA' cùng song song với mặt phẳng (BCC'B') nên hai mặt phẳng (ADD'A') và (BCC'B') song song với nhau.
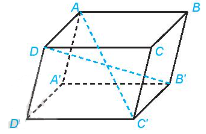
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C'.
a) Chứng minh rằng tứ giác AGG'A' là hình bình hành.
b) Chứng minh rằng AGC.A'G'C' là hình lăng trụ.
Trong không gian cho ba mặt phẳng phân biệt (P), (Q), (R). Những mệnh đề nào sau đây là đúng?
a) Nếu (P) chứa một đường thẳng song song với (Q) thì (P) song song với (Q).
b) Nếu (P) chứa hai đường thẳng song song với (Q) thì (P) song song với (Q).
c) Nếu (P) và (Q) song song với (R) thì (P) song song với (Q).
d) Nếu (P) và (Q) cắt (R) thì (P) và (Q) song song với nhau.
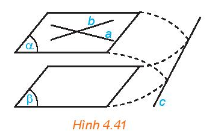
Cho mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) (H.4.41).
Nếu (α) và (β) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?

Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).

a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).
b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?