Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC). Tính d(SA, BC).
Giải bởi Vietjack
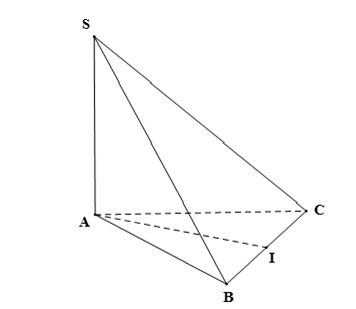
Gọi I là trung điểm của BC.
Xét ∆ABC đều có: AI là đường trung tuyến (do I là trung điểm của BC).
Suy ra AI ⊥ BC.
Do SA ⊥ (ABC) và AI ⊂ (ABC) nên SA ⊥ AI.
Ta có: AI ⊥ SA và AI ⊥ BC.
Suy ra đoạn thẳng AI là đoạn vuông góc chung của hai đường thẳng SA và BC.
Từ đó ta có d(SA, BC) = AI.
Xét ∆ABC đều cạnh a, có I là trung điểm của BC nên
Áp dụng định lí Pythagore vào tam giác ABI vuông tại I (do AI ⊥ BC) có:
AB2 = AI2 + BI2
Suy ra
Vậy
Cho hình tứ diện ABCD có AB = a, BC = b, BD = c, Gọi M, N, P lần lượt là trung điểm của AB, AC, AD (Hình 77).
a) Tính khoảng cách từ điểm C đến đường thẳng AB.
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).
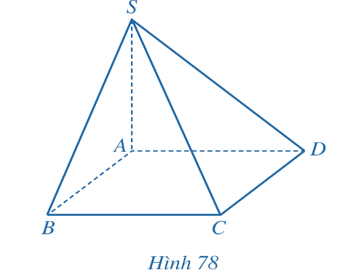
a) Tính khoảng cách từ điểm S đến đường thẳng CD.
b) Chứng minh rằng BD ⊥ (SAC) và tính khoảng cách giữa hai đường thẳng BD và SC.
Với giả thiết ở Bài tập 2, hãy:
a) Chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC.
Cho hình chóp S.ABC có SA = a, góc giữa SA và mp(ABC) là 60°. Gọi M, N lần lượt là trung điểm của cạnh SA và SB. Chứng minh MN // (ABC) và tính d(MN, (ABC)).
Cho hình chóp S.ABC có SA ⊥ (ABC), AI ⊥ BC (I ∈ BC), AH ⊥ SI (H ∈ SI). Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC) bằng AH.
Với giả thiết ở Bài tập 4, hãy:
a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD).
b) Chứng minh rằng MP // (BCD). Tính khoảng cách từ đường thẳng MP đến mặt phẳng (BCD).
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song Δ và ∆’. Xét điểm A trên đường thẳng Δ.
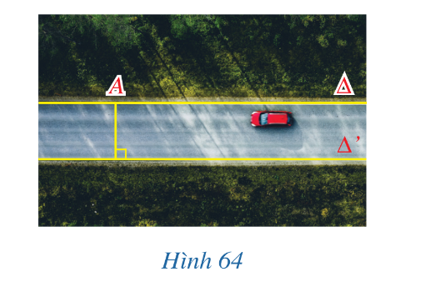
a) Khoảng cách từ điểm A đến đường thẳng Δ’ có phụ thuộc vào vị trí của điểm A trên đường thẳng Δ hay không? Vì sao?
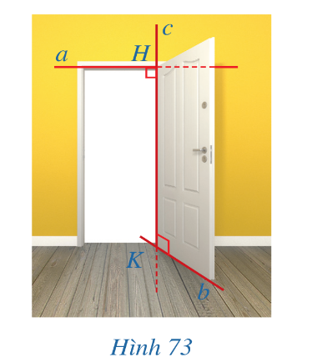
Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng a và b chéo nhau, hai bản lề của cánh cửa nằm trên đường thẳng c.
Quan sát Hình 73 và cho biết đường thẳng c có vừa cắt, vừa vuông góc với cả hai đường thẳng a và b hay không.
b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng Δ và mặt phẳng (P)?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
