 Giải bởi Vietjack
Giải bởi Vietjack
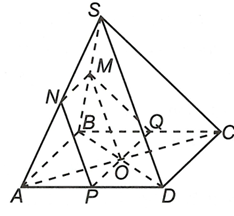
Ta có và
Mặt khác suy ra trong đó và
Ta lại có MO là đường trung bình của tam giác SBD nên
Suy ra và Oy cắt AD và BC lần lượt tại P, Q.
Vậy MNPQ là thiết diện của mặt phẳng với hình chóp S.ABCD.Phương pháp giải
Xác định lần lượt các giao tuyến của (P) với các mặt của hình chóp theo các bước sau:
- Từ điểm chung có sẵn , xác định giao tuyến đầu tiên của (P) với một mặt của hình chóp (Có thể là mặt trung gian)
- Cho giao tuyến này cắt các cạnh của mặt đó của hình chóp ta sẽ được các điểm chung mới của (P) với các mặt khác . Từ đó xác định được các giao tuyến mới với các mặt này
- Tiếp tục như thế cho tới khi các giao tuyến khép kín ta được thiết diện .
Sử dụng định lí: Hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng song song với 2 đường thẳng đó:
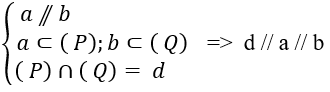
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc đoạn SB (M không trùng với S và B). Mặt phẳng cắt hình chóp S.ABCD theo thiết diện là
A. hình bình hành
B. tam giác
C. hình chữ nhật
D. hình thang
Cách giải:
Đáp án D
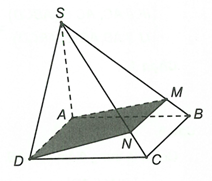
Ta có M là một điểm thuộc đoạn SB với M khác S và B.
Suy ra
sao cho
Gọi thì cắt hình chóp S.ABCD theo thiết diện là tứ giác AMND. Vì và MN với AD không bằng nhau nên tứ giác AMND là hình thang.
Tham khảo thêm một số tài liệu liên quan:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi H và K lần lượt là trung điểm các cạnh CB và CD, M là điểm bất kì trên cạnh SA. Dựng thiết diện của hình chóp với mặt phẳng (MHK)
Cho tứ diện ABCD có AB vuông góc với CD, tam giác BCD vuông tại C và góc M là một điểm thay đổi trên cạnh BD; đặt Mặt phẳng đi qua M và song song với AB, CD.
a) Dựng thiết diện của tứ diện với