A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
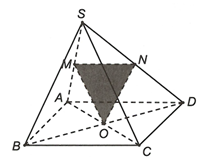
Ta có
Lý thuyết Hai mặt phẳng song song
Cho hai mặt phẳng (P) và (Q), có thể xảy ra một trong ba trường hợp:
• Trường hợp 1: (P) và (Q) có ba điểm chung không thẳng hàng, ta nói hai mặt phẳng (P) và (Q) trùng nhau.
Kí hiệu: (P) = (Q)
• Trường hợp 2: (P) và (Q) phân biệt và có một điểm chung, ta nói (P) và (Q) cắt nhau theo giao tuyến d đi qua điểm chung.
Kí hiệu: (P) (Q) = d
• Trường hợp 3: (P) và (Q) không có bất kì điểm chung nào, nghĩa là (P) (Q) = , ta nói (P) và (Q) song song.
Kí hiệu: (P) // (Q) hoặc (Q) // (P)
Chứng minh rằng
Cách giải:
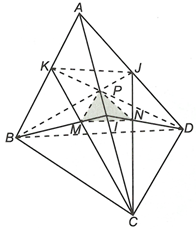
Gọi I, J, K lần lượt là trung điểm AC, AD, AB.
Xét có nên
Suy ra
Xét có nên
Suy ra
Ta có
Tham khảo thêm một số tài liệu liên quan:
Chuyên đề Hai mặt phẳng song song 2024 hay, chọn lọc
Chuyên đề Đường thẳng và mặt phẳng song song 2024 hay, chọn lọc
Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của
Chứng minh rằng