Cho hình chóp đều S.ABC có cạnh đáy bằng a căn 3. Tính khoảng cách từ điểm A đến SBC biết thể tích khối chóp S.ABC bằng...

Question

Cho hình chóp đều S.ABC có cạnh đáy bằng a3. Tính khoảng cách từ điểm A đến (SBC) biết thể tích khối chóp S.ABC bằng a364.

VietJack · Accepted Answer

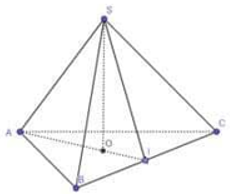
Đáp án C Gọi O là trọng tâm tam giác ABC và I là trung điểm của đoạn thẳng BC Tam giác ABC đều cạnh a3 nên SΔABC=3a234 và chiều cao AI=3a2 OI=13AI=133a2=a2. Thể tích của khối chóp S.ABC=12SΔABC.SO⇔a364=12.3a234.SO⇔SO=2a SI=SO2+OI2=2a2+a24=3a2 SΔSBC=12.SI.BC=12.3a2.a3=3a234 Gọi khoảng cách từ điểm A đến mặt phẳng (SBC) là h Thể tích của khối chóp S.ABC=12.SΔSBC.h⇔a364=13.3a234.h⇔h=a2. Phương pháp giải Để tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α) Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α) Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒(α) ⊥ (SAK) và (α) ∩ (SAK) = SK Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d(A, (α)) = AP Bài tập liên quan: Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoảng cách từ O đến mặt phẳng (SBC) bằng A. a66 . B. a33 . C. a32 . D. a36 . Cách giải: Tham khảo thêm một số tài liệu liên quan: Đề thi tham khảo Toán 2024 Đề thi thử Toán 2024 phát triển từ đề tham khảo

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Cho hình chóp đều S.ABC có cạnh đáy bằng $a \sqrt{3} .$ Tính khoảng cách từ điểm A đến $(S B C)$ biết thể tích khối chóp S.ABC bằng $\frac{a^{3} \sqrt{6}}{4} .$

A. $\frac{a \sqrt{2}}{2} .$

B. $a .$

C. $a \sqrt{2} .$

D. $\frac{2 a \sqrt{3}}{3} .$

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Biết SA vuông góc với mặt phẳng đáy và $\hat{S B A} = 30^{0} .$ Thể tích khối chóp $S . A B C$ bằng

Câu 2:

Gọi $M, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{1}{3} x^{3} - 2 x^{2} + 3 x - \frac{1}{3}$ trên đoạn $[0; 2] .$ Tính tổng $S = M + m .$

Câu 3:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Số giá trị nguyên của tham số m để phương trình $f (x^{2} - 4 x) = m$ có ít nhất 3 nghiệm thực phân biệt thuộc khoảng $(0; + \infty)$ là

Câu 4:

Tìm tất cả giá trị thực của tham số m sao cho đồ thị của hàm số $y = 2 x^{3} - (2 + m) x + m$ cắt trục hoành tại 3 điểm phân biệt

Câu 5:

Cho hàm số $y = f (x) .$ Hàm số $y = f' (x)$ có đồ thị như hình vẽ:

Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m sao cho hàm số $y = f (x - m)$ đồng biến trên khoảng $(2020; + \infty) .$ Số phần tử của tập S là

Câu 6:

Cho hàm số trùng phương $y = a x^{4} + b x^{2} + c$ có đồ thị như hình vẽ. Hỏi đồ thị hàm số $y = \frac{x^{4} + 2 x^{3} - 4 x^{2} - 8 x}{{[f (x)]}^{2} + 2 f (x) - 3}$ có tổng cộng bao nhiêu tiệm cận đứng?

Câu 7:

Gọi S là tập tất cả các giá trị nguyên của tham số để hàm số $y = x^{4} - (m^{2} - 9) x^{2} + 2021$ có 1 cực trị. Số phần tử của tập S là

Câu 8:

Một chất điểm chuyển động theo phương trình $S = - t^{3} + 3 t^{2} - 2,$ trong đó t tính bằng giây và S tính theo mét. Vận tốc lớn nhất của chuyển động chất điểm đó là

Câu 9:

Câu 10:

Cho hình chóp $S . A B C D$ có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm =AD và BC. Giao tuyến của hai mặt phẳng $(S M N)$ và $(S A C)$ là

Câu 11:

Cho hàm số $f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ)$ có đồ thị như sau

Trong các số $a, b, c, d$ có bao nhiêu số dương?

Câu 12:

Giá trị của m để hàm số $y = \frac{\cot x - 2}{\cot x - m}$ nghịch biến trên $(\frac{π}{4}; \frac{π}{2})$ là

Câu 13:

Cho hình lăng trụ đứng $A B C . A' B' C'$ có đáy ABC là tam giác đều cạnh a. Cạnh bên $A A' = a \sqrt{2} .$ Khoảng cách giữa hai đường thẳng A'B và B'C là

Câu 14:

Cho hình chóp S.ABC có $S A ⊥ (A B C)$ và H là hình chiếu vuông góc của S lên BC. Khi đó BC vuông góc với đường thẳng nào sau đây?

Đề thi liên quan

Câu hỏi mới nhất

Câu hỏi:

Cho hình chóp đều S.ABC có cạnh đáy bằng a3. Tính khoảng cách từ điểm A đến (SBC) biết thể tích khối chóp S.ABC bằng a364.

A.a22.

B.a.

C.a2.

D.2a33.