Cho hàm số $y=\frac{1}{4}\left(8m^3-1\right)x^4-2x^3+\left(2m-7\right)x^2-12x+2018$  với m là tham số. Số các giá trị nguyên m thuộc đoạn $\left[-2018;2018\right]$  để hàm số đã cho đồng biến trên $\left[\frac{-1}{2};\frac{-1}{4}\right]$  là

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số $y=\frac{1}{4}{x}^4+mx-\frac{3}{2x}$  đồng biến trên khoảng $\left(0;+\infty \right)$ ?

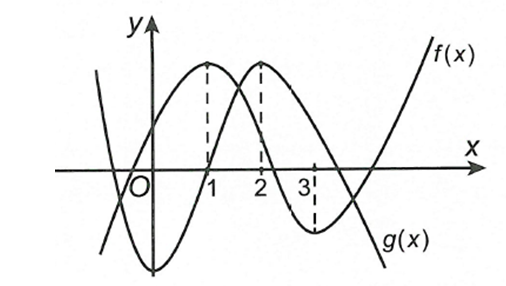
Cho hai hàm số $f\left(x\right)$  và  $g\left(x\right)$có đồ thị như hình vẽ. Biết rằng hai hàm số $f\left(2x-1\right)$  và $g\left(ax+b\right)$  có cùng khoảng nghịch biến $\left(m;n\right)$ , $m,n\in \mathbb{N}$ . Khi đó giá trị của biểu thức $\left(4a+b\right)$  bằng

Cho hàm số $y=\left|x^3-3x^2+2+m\right|$ . Gọi S là tập hợp tất cả các số nguyên $m\in \left[-2019;2020\right]$  sao cho hàm số đồng biến trên $\left(3;+\infty \right)$ . Số các phần tử của S bằng

Cho hàm số $y=f\left(x\right)$  xác định trên khoảng $\left(0;3\right)$  có tính chất

$f^{\text{'}}\left(x\right)\ge 0,\forall x\in \left(0;3\right)$và$f^{\text{'}}\left(x\right)=0$, $\forall x\in \left(1;2\right)$.

Tìm khẳng định đúng trong các khẳng định sau.

Cho hàm số $y=\left|x^3-mx+1\right|$ . Gọi S là tập hợp các số tự nhiên m sao cho hàm số đồng biến trên $\left[1;+\infty \right)$ . Tổng các phần tử của S bằng

Có bao nhiêu giá trị nguyên không âm của tham số m sao cho hàm số $y=-x^4+\left(2m-3\right)x^2+m$  nghịch biến trên đoạn $\left[1;2\right]$ ?

Cho hàm số $y=f\left(x\right)$  xác định trên tập R và có $f^{\text{'}}\left(x\right)=x^2-5x+4$ . Khẳng định nào sau đây đúng?

Gọi S là tập hợp các giá trị thực của tham số  để hàm số $y=\frac{1}{3}{x}^3-\frac{1}{2}{x}^2+2mx-3m+4$  nghịch biến trên một đoạn có độ dài bằng 3. Tổng tất cả các phần tử của S bằng

Gọi S là tập hợp các giá trị của tham số m để hàm số

$f\left(x\right)=\frac{1}{5}{m}^2{x}^5-\frac{1}{3}m{x}^3+10x^2-\left(m^2-m-20\right)x$ đồng biến trên R .

Tổng giá trị của tất cả các phần tử thuộc S bằng 

Có bao nhiêu giá trị nguyên của tham số $m\in \left(-10;10\right)$  để hàm số $y=\frac{1-2\sin x}{2\sin x+m}$  đồng biến trên khoảng $\left(\frac{\pi }{2};\pi \right)$ ?

Có bao nhiêu giá trị nguyên của tham số m trong khoảng $\left(-2018;2018\right)$  để hàm số $y=\left(2m-1\right)x-\left(3m+2\right)\cos x$  nghịch biến trên R ?

Có bao nhiêu giá trị nguyên của tham số $m\in \left[-2018;2018\right]$  để hàm số $y=\sqrt{x^2+1}-mx-1$  đồng biến trên $\left(-\infty ;+\infty \right)$ .

Tìm các giá trị của  m để hàm số $y=x^3\left(x^3-2mx+m^2-m-6\right)$  không đổi dấu khi đi qua x=0.