Cho hàm số $y=f\left(x\right)=a{x}^4+b^2{x}^2+1(a\not\equiv 0)$ Trong các khẳng định dưới đây, khẳng định nào là đúng?

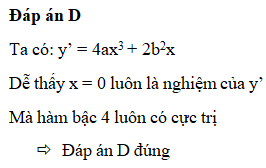
Cho hàm số $y= x^4-2(2m+1)x^2+4m^2 \left(1\right)$. Các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ $x_1,x_2,x_3,x_4$  thỏa mãn  là ${x_1}^2+{x_2}^2+{x_3}^2+{x_4}^2=6$

Đồ thị hàm số $y=\frac{x-3}{x^2+x-2}$  có bao nhiêu đường tiệm cận đứng?

Cho hàm số $y=x^3+3x^2+m$có đồ thị (C). Để đồ thị cắt trục hoành tại 3 điểm A , B , C sao cho C là trung điểm của AC thì giá trị tham số m là:

Cho hình tứ diện ABCD có DA=BC=5,AB=3,AC=4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện  là:

Cho hình chóp tam giác S.ABC có M,N lần lượt là trung điểm của các cạnh SA và SB . Tỉ số $\frac{V_{S.CMN}}{V_{S.CAB}}$ là:

Có bao nhiêu tiếp tuyến với đồ thị (C):$y=x^4-2x^2$ đi qua gốc tọa độ O?

Cho hàm số $y=\frac{2x-1}{x-1}\left(C\right)$ . Hệ số góc của tiếp tuyến với đồ thị sao cho tiếp tuyến đó cắt trục Ox , Oy lần lượt tại các điểm A , B thỏa mãn  OA=4OB là:

Hàm số $y=-x^4-x^2+3$ nghịch biến trên:

Hàm số $y=x^3-3x^2+4$ đạt cực tiểu tại:

Giả sử tiếp tuyến của đồ thị hàm số $y=2x^3-6x^2+18x+1$  song song với đường thẳng d:12x - y = 0 có dạng là y = ax + b . Khi đó tổng a+b là

Cho hàm số $y=\frac{x+2}{x-3}$ có đồ thị (C). Có bao nhiêu tiêu điểm  thuộc sao cho khoảng cách từ điểm đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm  đến tiệm cận đứng.

Cho hàm số y=f(x)  có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?

Cho hàm số $y=\frac{2x^2-3x+m}{x-m}$  Để đồ thị hàm số không có tiệm cận đứng thì các giá trị 

Tìm GTLN và GTNN của hàm số $y=x^5-5x^4+5x^3+1$ trên đoạn [-1;2]