Giải bởi Vietjack
Lời giải
Diện tích xung quanh của hình chóp tam giác đều S.ABC là:
\(\frac{1}{2}.\left( {3a} \right).d = \frac{1}{2}.3.2a'.d = 3a'd\) (đơn vị diện tích).
Diện tích xung quanh của hình chóp tam giác đều S’.A’B’C’ là:
\(\frac{1}{2}.\left( {3a'} \right).d' = \frac{3}{2}a'd'\) (đơn vị diện tích).
Do diện tích xung quanh của S.ABC gấp k lần diện tích xung quanh của S’.A’B’C’ nên ta có: \(3a'.d = k.\frac{3}{2}a'.d'\).
Suy ra \(\frac{d}{{d'}} = \frac{k}{2}\).
Vậy tỉ số giữa d và d’ là \(\frac{k}{2}\).
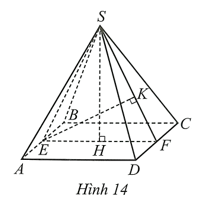
Trong các phát biểu sau, phát biểu nào sai?
a) Đường cao kẻ từ đỉnh trong mỗi mặt bên của hình chóp tứ giác đều được gọi là trung đoạn của hình chóp tứ giác đều đó.
b) Hình chóp tam giác đều là hình chóp có mặt đáy là tam giác vuông.
c) Mỗi mặt bên của hình chóp tam giác đều là tam giác cân.
d) Hình chóp tứ giác đều là hình chóp có mặt đáy là hình vuông.
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?
a) Nếu độ dài trung đoạn của một hình chóp tứ giác đều tăng lên n lần (n > 1) và độ dài cạnh đáy không đổi thì diện tích xung quanh của hình chóp tứ giác đều đó cũng tăng lên n lần.
b) Nếu độ dài cạnh đáy của một hình chóp tứ giác đều tăng lên n lần (n > 1) và chiều cao không đổi thì thể tích của hình chóp tứ giác đều đó cũng tăng lên n lần.
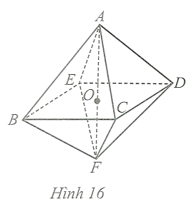
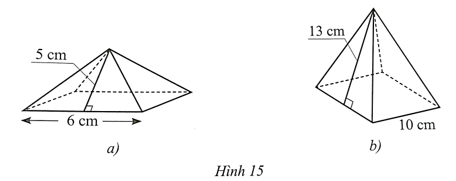
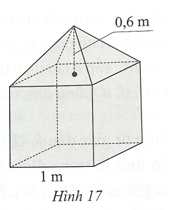
Cho hình chóp tam giác đều S.ABC có độ dài trung đoạn bằng x (dm) và độ dài cạnh đáy bằng 2x (dm). Diện tích xung quanh của hình chóp tam giác đều S.ABC là:
A. x2 (dm2).
B. 2x2 (dm2).
C. 3x2 (dm2).
D. 4x2 (dm2).
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng a (cm) và chiều cao bằng 3a (cm). Thể tích của hình chóp đó là:
A. 3a3 (cm2).
B. a3 (cm2).
C. 3a3 (cm3).
D. a3 (cm3).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
