Cho a+b+c=pi/2 và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng...

Question

Cho a+b+c=π2 và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng

VietJack · Accepted Answer

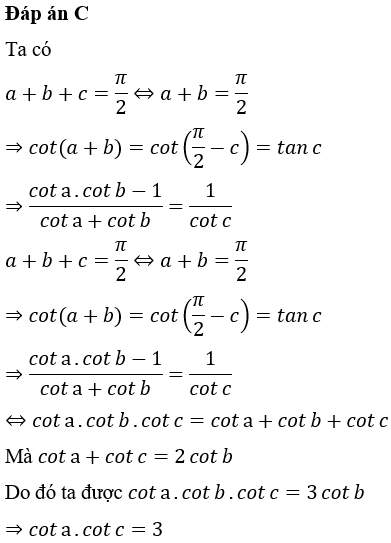
Giá trị lượng giác của một góc Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để . - Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho xOM^ = α. Khi đó: + sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α; + côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α; + Khi α ≠ 90° (hay x0 ≠ 0), tang của α là y0x0 , được kí hiệu là tan α; + Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là x0y0 , được kí hiệu là cot α. - Từ định nghĩa trên ta có: tanα=sinαcosα(α≠90°); cotα=cosαsinα(α≠0°vàα≠180°); tanα=1cotα(α∉{0°;90°;180°}) - Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt: Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định. Xem thêm một số kiến thức liên quan: Những bài tập trắc nghiệm hay về chuyên đề Cung và góc Lượng giác Tổng hợp kiến thức và bài tập trắc nghiệm có đáp án chi tiết chuyên đề Cung và góc lượng giác

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Cho a+b+c= $\frac{π}{2}$ và cota, cotb, cotc tạo thành cấp số cộng. Gía trị cota.cotc bằng

A. 1

B. 2

C. 3

D. 4

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Đường thẳng y= 6x+m là tiếp tuyến của đường cong $y = x^{3} + 3 x - 1$ khi m bằng

Câu 2:

Tìm số các ước dương không nhỏ hơn 1000 của số 490000

Câu 3:

Cho hàm số $y = \frac{2 x - 1}{2 x + 3}$ có đồ thị là (C). Gọi M là giao điểm của (C) và trục hoành. Khi đó tích các khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) bằng

Câu 4:

Bên cạnh hình vuông ABCD có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với ABCD. Biết rằng bốn tam giác là bốn tam giác cân. “Hỏi tổng diện tích của vuông ở giữa và bốn tam giác cân nhỏ nhất bằng bao nhiêu?”

Câu 5:

Hàm số y= f(x) xác định, liên tục trên R và đạo hàm $f' (x) = 2 (x - 1)^{2} (2 x + 6)$ . Khi đó hàm số f(x)

Câu 6:

Cho các số hạng dương a, b, c là số hạng thứ m, n, p của một cấp số cộng và một cấp số nhân. Tính giá trị của biểu thức $\log_{2} a^{b - c} b^{c - a} c^{a - b}$

Câu 7:

Tính đạo hàm của hàm số $y = 3 . e^{- x} + 2017 e^{c o s x}$

Câu 8:

Cho dãy số $\{\begin{cases} u_{1} = 2018 \\ u_{n - 1} = n^{2} (u_{n - 1} - u_{n}) \end{cases} (n \in N^{*})$ . Tính lim $u_{n}$ ⁡

Câu 9:

Cho bất phương trình $\log_{4} x . l o g_{2} (4 x) + \log_{\sqrt{2}} (x^{3} / 2) > 0$ . Nếu đặt $t = l o g_{2} x$ , ta được bất phương trình nào sau đây

Câu 10:

Tính diện tích S của hình phẳng giới hạn bởi hai đường cong $y = x^{3} - x v à y = x - x^{2}$

Câu 11:

Hình bên gồm đường tròn bán kính 3 và elip có độ dài trục lớn là 6, độ dài trục bé bằng 4 cắt nhau. Biết chiều dài nhất của hình bằng 11, tính diện tích của hình này

Câu 12:

Hàm số nào dưới đây đồng biến trên R

Câu 13:

Trong các khẳng định sau, khẳng định nào là sai

Câu 14:

Với phép vị tự tâm O tỉ số k= -1 biến đường tròn (C): $x^{2} + y^{2} = 9$ thành đường tròn có phương trình nào sau đây?

Đề thi liên quan

Câu hỏi mới nhất