Lời giải bài tập Vật Lí lớp 10 Bài 9: Chuyển động thẳng biến đổi đều sách Kết nối tri thức ngắn gọn, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Vật Lí 10 Bài 9 từ đó học tốt môn Lí 10.

Giải bài tập Vật lí lớp 10 Bài 9: Chuyển động thẳng biến đổi đều

Video bài giảng Chuyển động thẳng biến đổi đều - Kết nối tri thức

Giải vật lí 10 trang 40 Tập 1 Kết nối tri thức

I. Gia tốc của chuyển động thẳng biến đổi đều 

Câu hỏi 1 trang 40 Vật Lí 10: Tính gia tốc của các chuyển động trong hình vẽ ở đầu bài.

Phương pháp giải:

Sử dụng công thức tính gia tốc: $a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}$

Lời giải:

- Gia tốc của ô tô là:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{10}{1}=10\left(m/s^2\right)$

- Gia tốc của người chạy bộ là:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{4-6}{1-0}=-2\left(m/s^2\right)$

Câu hỏi 2 trang 40 Vật Lí 10: Các chuyển động trong hình vẽ ở đầu bài có phải là chuyển động thẳng biến đổi đều hay không?

Phương pháp giải:

Chuyển động thẳng biến đổi đều là chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm đều theo thời gian.

Lời giải:

Chuyển động thẳng biến đổi đều là chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm đều theo thời gian.

=> Các chuyển động trong hình vẽ ở đầu bài là chuyển động thẳng biến đổi đều.

Giải vật lí 10 trang 41 Tập 1 Kết nối tri thức

III. Đồ thị vận tốc - thời gian của chuyển động thẳng biến đổi đều 

Câu hỏi 1 trang 41 Vật Lí 10: Từ các đồ thị trong hình 9.1:

a) Hãy viết công thức về mối liên hệ giữa v với a và t của từng chuyển động ứng với từng đồ thị trong hình 9.1.

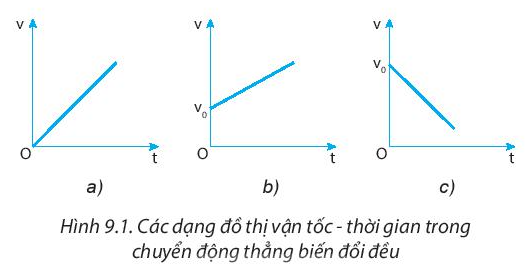
b) Chuyển động nào là chuyển động nhanh dần đều, chậm dần đều?

Phương pháp giải:

Dựa vào các đồ thị hình 9.1.

Lời giải:

a)

- Đồ thị a: $v=at$

- Đồ thị b: $v=v_0+at$

- Đồ thị c: $v=v_0-at$

b)

- Chuyển động nhanh dần đều là: đồ thị a và b

- Chuyển động chậm dần đều: đồ thị c

Câu hỏi 2 trang 41 Vật Lí 10: Hình 9.2 là đồ thị vận tốc – thời gian trong chuyển động của một bạn đang đi trong siêu thị. Hãy dựa vào đồ thị để mô tả bằng lời chuyển động của bạn đó (khi nào đi đều, đi nhanh lên, đi chậm lại, nghỉ).

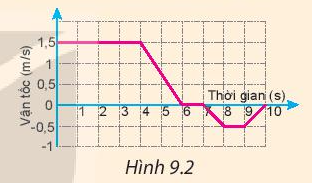
Phương pháp giải:

Sử dụng kĩ năng đọc đồ thị.

Lời giải:

- Trong 4 s đầu tiên: bạn đó đi đều với vận tốc 1,5 m/s.

- Từ giây 4 – giây 6: bạn đó đi chậm lại.

- Từ giây 6 đến giây 7: bạn đó nghỉ

- Từ giây 7 đến giây 8: bạn đó bắt đầu đi theo chiều âm

- Từ giây 8 – 9: bạn đó đi đều với vận tốc -0,5 m/s.

- Từ giây 9 – 10: đi chậm và dừng lại tại giây thứ 10.

Giải vật lí 10 trang 42 Tập 1 Kết nối tri thức

IV. Độ dịch chuyển của chuyển động thẳng biến đổi đều 

Câu hỏi 1 trang 42 Vật Lí 10: Hãy tính độ dịch chuyển của chuyển động có đồ thị (v-t) vẽ ở Hình 9.3b. Biết mỗi cạnh của ô vuông nhỏ trên trục tung ứng với 2 m/s, trên trục hoành ứng với 1 s.

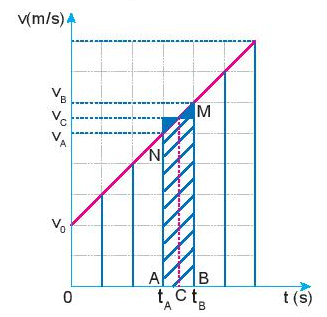
Phương pháp giải:

Dựa vào đồ thị hình 9.3b.

Lời giải:

Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.

Từ đồ thị ta có: $\{\begin{array}{l}{v}_0=4\left(m/s\right);v=16\left(m/s\right)\\ t=6\left(s\right)\end{array}$

Suy ra: Độ dịch chuyển là:

$d=\frac{\left(4+16\right).6}{2}=60\left(m\right)$

Câu hỏi 2 trang 42 Vật Lí 10: Chứng tỏ rằng có thể xác định được giá trị của gia tốc dựa trên đồ thị (v - t). 

Phương pháp giải:

Dựa vào đồ thị hình 9.3b.

Lời giải:

Ta có: Gia tốc: $a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}$

Từ đồ thị ta thấy: Độ biến thiên vận tốc các khoảng thời gian bằng nhau là 2 m/s.

Xét giữa 2 thời điểm A và B:

=> $a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{v_B-v_A}{t_A-t_B}=\frac{12-8}{4-3}=\frac{2}{1}=2(m/s^2)$

Vậy có thể xác định được giá trị của gia tốc dựa trên đồ thị v – t.

Câu hỏi 1 trang 42 Vật Lí 10: Biết độ dịch chuyển trong chuyển động thẳng biến đổi đều có độ lớn bằng diện tích giới hạn đồ thị (v – t) trong thời gian t của chuyển động và các trục tọa độ. Hãy chứng minh rằng công thức tính độ lớn của độ dịch chuyển trong chuyển động thẳng biến đổi đều là:

$d=v_{0}t+\frac{1}{2}a{t}^2$     (9.4)

Lời giải:

Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.

Diện tích hình thang: $d=s_{ht}=\frac{(v+v_0).t}{2}=\frac{1}{2}{v}_{0}t+\frac{1}{2}vt$     (1)

Lại có: $a=\frac{v-v_0}{t}\Rightarrow v=at+v_0$      (2)

Thay (2) vào (1) ta được:

$d=\frac{1}{2}{v}_{0}t+\frac{1}{2}(at+v_0)t=\frac{1}{2}{v}_{0}t+\frac{1}{2}a{t}^2+\frac{1}{2}{v}_{0}t$

$\Rightarrow d=v_{0}t+\frac{1}{2}a{t}^2$      (đpcm)

Câu hỏi 2 trang 42 Vật Lí 10: Từ công thức (9.2) và (9.4) chứng minh rằng:

$v^2-v_0^2=2.a.d$                (9.5)

Lời giải:

Ta có: $v_t=v_0+at$   (9.2)

$d=v_{0}t+\frac{1}{2}a{t}^2$     (9.4)

+ Bình phương 2 vế của (9.2) ta được:

$v^2=v_0^2+2v_0.at+a^2{t}^2=v_0^2+a(2v_{0}t+a{t}^2)$          (1)

+ Từ (9.4) ta có:

$2\mathrm{d}=2v_{0}t+a{t}^2$       (2)

Thay (2) vào (1) ta được:

$v^2=v_0^2+a.2\mathrm{d}\iff v^2-v_0^2=2\mathrm{a}.d$   (đpcm)

Câu hỏi trang 42 Vật Lí 10: Hãy dùng đồ thị (v – t) vẽ ở hình 9.4 để:

a) Mô tả chuyển động

b) Tính độ dịch chuyển trong 4 giây đầu, 2 giây tiếp theo và 3 giây cuối

c) Tính gia tốc của chuyển động trong 4 giây đầu

d) Tính gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6.

Kiểm tra kết quả của câu b và câu c bằng cách dùng công thức.

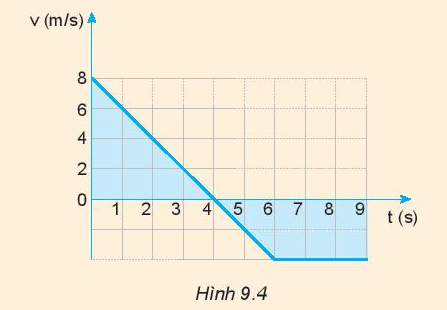
Phương pháp giải:

- Dựa vào đồ thị hình 9.4 để mô tả chuyển động.

- Sử dụng công thức tính độ dịch chuyển, gia tốc.

Lời giải:

a) Mô tả chuyển động:

- Trong 4 giây đầu tiên: chuyển động chậm dần đều từ 8 m/s đến 0 m/s

- Từ giây thứ 4 đến giây thứ 6: bắt đầu tăng tốc với vận tốc -2 m/s

- Từ giây thứ 6 đến giây thứ 9: chuyển động thẳng đều với vận tốc – 2 m/s

b) Độ dịch chuyển:

- Trong 4 giây đầu:

Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.

$d_1=\frac{1}{2}.t_1.v_1=\frac{1}{2}.4.8=16\left(m\right)$

- Trong 2 giây tiếp theo:

Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.

$d_2=\frac{1}{2}.t_2.v_2=\frac{1}{2}.2.(-4)=-4\left(m\right)$

- Trong 3 giây cuối:

Độ dịch cuyển bằng diện tích hình chữ nhật có chiều dài là t và chiều rộng là v.

$d_3=v_3.t_3=-4.3=-12\left(m\right)$

c)

Gia tốc của chuyển động trong 4 giây đầu:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{8-0}{4-0}=2\left(m/s^2\right)$

d)

Gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{-4-0}{6-4}=-2\left(m/s^2\right)$

* Kiểm tra kết quả bằng công thức:

Độ dịch chuyển:

- Trong 4 giây đầu:

$d_1=v_0{t}_1+\frac{1}{2}a{t_1}^2=0.4+\frac{1}{2}.2{.4}^2=16\left(m\right)$

- Trong 2 giây tiếp theo:

$d_2=v_0{t}_2+\frac{1}{2}a{t_2}^2=0.2+\frac{1}{2}.(-2){.2}^2=-4\left(m\right)$

- Trong 3 giây cuối:

$d_3=v_{3}t=-4.3=-12\left(m\right)$

=> Trùng với kết quả khi dùng đồ thị. 

Giải vật lí 10 trang 43 Tập 1 Kết nối tri thức

Bài tập vận dụng

Bài 1 trang 43 Vật Lí 10: Đồ thị vận tốc – thời gian ở Hình 9.5 mô tả chuyển động của một chú chó con đang chạy trong một ngõ thẳng và hẹp.

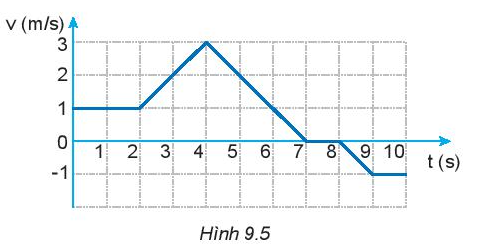
a) Hãy mô tả chuyển động của chú chó.

b) Tính quãng đường đi được và độ dịch chuyển của chú chó sau: 2s; 4s; 7s và 10s bằng đồ thị và bằng công thức.

Phương pháp giải:

- Dựa vào đồ thị hình 9.5.

- Sử dụng công thức tính độ dịch chuyển, gia tốc.

Lời giải:

a) Mô tả chuyển động:

- Trong 2 giây đầu tiên: chuyển động thẳng đều với vận tốc 1 m/s.

- Từ giây thứ 2 đến giây thứ 4: chuyển động nhanh dần đều

- Từ giây 4 đến giây 7: chuyển động chậm dần

- Từ giây 4 đến giây 8: dừng lại

- Từ giây 8 đến giây 9: chuyển động nhanh dần theo chiều âm

- Từ giây 9 đến giây 10 chuyển động thẳng đều với vận tốc -1 m/s.

b) Quãng đường đi được và độ dịch chuyển:

- Sau 2 giây:

$s_1=d_1=v_1{t}_1=1.2=2\left(m/s\right)$

- Sau 4 giây:

$s_2=d_2=s_1+\frac{1}{2}(1+3).2=2+4=6\left(m\right)$

- Sau 7 giây:

+ Quãng đường:

$s_3=s_2+\frac{1}{2}.3.\left(7-4\right)=6+4,5=10,5\left(m\right)$

+ Độ dịch chuyển:

$d_3=d_2+\frac{1}{2}.(3).\left(7-4\right)=6+4,5=10,5\left(m\right)$

- Sau 10 giây:

+ Quãng đường:

$s_4=s_3+s^{\prime }=10,5+0,5+1=12\left(m\right)$

+ Độ dịch chuyển:

$d_4=d_3+d^{\prime }=10,5-0,5-1=9\left(m\right)$

* Kiểm tra bằng công thức:

- Sau 2 giây:

$s_1=d_1=v_1{t}_1=1.2=2\left(m/s\right)$

- Sau 4 giây:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{3-1}{4-2}=\frac{2}{2}=1\left(m/s^2\right)$

$s_2=d_2=d_1+v_1{t}_1+\frac{1}{2}a{t}_1^2=2+1.2+\frac{1}{2}.1{.2}^2=6\left(m\right)$

- Sau 7 giây:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\frac{0-3}{7-4}=\frac{2}{2}=-1\left(m/s^2\right)$

+ Quãng đường và độ dịch chuyển từ giây 4 đến giây 7 là:

$d^{\prime }=s^{\prime }=v_{0}t+\frac{1}{2}a{t}^2=3.3+\frac{1}{2}(-1).(7-4{)}^2=4,5\left(m\right)$

=> Quãng đường và độ dịch chuyển đi được sau 7 giây là:

$d_3=s_3=d_2+d^{\prime }=6+4,5=10,5\left(m\right)$

- Sau 10 giây:

+ Từ giây 7 – 8: đứng yên

+ Từ giây 8 – 9:

$a=\frac{-1-0}{9-8}=-1\left(m/s^2\right)$

$d=v_{0}t+\frac{1}{2}a{t}^2=0.1+\frac{1}{2}\left(-1\right){.1}^2=-0,5\left(m\right)$

s = 0,5 m

+ Từ giây 9 – 10:

$d=vt=-1.1=-1\left(m\right)$

s = 1 m

Suy ra: độ dịch chuyển và quãng đường đi được sau 10 giây lần lượt là:

$d_4=d_3-0,5-1=10,5-0,5-1=9\left(m\right)$

$s_4=s_3-0,5-1=10,5+0,5+1=12\left(m\right)$

=> Kiểm tra thấy các kết quả trùng nhau.

Bài 2 trang 43 Vật Lí 10: Một vận động viên đua xe đạp đường dài vượt qua vạch đích với tốc độ 10 m/s. Sau đó vận động viên này đi chậm dần đều thêm 20 m mới dừng lại. Coi chuyển động của vận động viên là thẳng.

a) Tính gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích.

b) Tính thời gian vận động viên đó cần để dừng lại kể từ khi cán đích.

c) Tính vận tốc trung bình của người đó trên quãng đường dừng xe.

Phương pháp giải:

Sử dụng các công thức tính gia tốc, thời gian, vận tốc.

Lời giải:

a)

Gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích là:

$v^2-v_0^2=2\mathrm{a}\mathrm{d}\iff a=\frac{v^2-v_0^2}{2\mathrm{d}}=\frac{0^2-{10}^2}{2.20}=-2,5\left(m/s^2\right)$

b)

Thời gian vận động viên đó cần để dừng lại kể từ khi cán đích là:

$a=\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}\iff \mathrm{\Delta }t=\frac{\mathrm{\Delta }v}{a}=\frac{0-10}{-2,5}=4\left(s\right)$

c)

Vận tốc trung bình của người đó trên quãng đường dừng xe là:

$v=\frac{d}{t}=\frac{20}{4}=5\left(m/s\right)$

Xem thêm các bài giải SGK Vật lí lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 8: Chuyển động biến đổi. Gia tốc

Bài 10: Sự rơi tự do

Bài 11: Thực hành: Đo gia tốc rơi tự do

Bài 12: Chuyển động ném

Lý thuyết Chuyển động thẳng biến đổi đều

I. Gia tốc của chuyển động thẳng biến đổi đều

- Chuyển động thẳng biến đổi đều là chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm đều theo thời gian.

- Chuyển động thẳng có độ lớn vận tốc tăng đều theo thời gian gọi là chuyển động thẳng nhanh dần đều.

Thả viên bi dọc theo máng nghiêng, từ A đến C viên bi

Chuyển động thẳng nhanh dần đều

- Chuyển động thẳng có độ lớn vận tốc giảm đều theo thời gian gọi là chuyển động thẳng chậm dần đều.

Tàu lửa sắp về bến là chuyển động chậm dần đều

- Chuyển động thẳng biến đổi đều có vận tốc thay đổi đều theo thời gian nên gia tốc chuyển động này không đổi theo thời gian

$\text{a = }\frac{\mathrm{\Delta v}}{\mathrm{\Delta t}}$= hằng số

II. Vận tốc tức thời của chuyển động thẳng biến đổi đều

Gọi ${\text{v}}_{\mathrm{o}}$ là vận tốc tại thời điểm ban đầu ${\mathrm{t}}_{\mathrm{o}}$, ${\text{v}}_{\mathrm{t}}$ là vận tốc tại thời điểm t

Vì $\text{a = }\frac{\mathrm{\Delta v}}{\mathrm{\Delta t}}\text{ = }\frac{{\mathrm{v}}_{\mathrm{t}}-{\mathrm{v}}_{\mathrm{o}}}{\mathrm{\Delta t}}$ nên ${\mathrm{v}}_{\mathrm{t}}={\mathrm{v}}_{\mathrm{o}}+\text{ a}.\mathrm{\Delta t}$

- Nếu ${\mathrm{t}}_{\mathrm{o}}=0$ thì ${\mathrm{v}}_{\mathrm{t}}={\mathrm{v}}_{\mathrm{o}}+\text{ a}.\mathrm{t}$

- Nếu ${\mathrm{t}}_{\mathrm{o}}=0$ và ${\mathrm{v}}_{\mathrm{o}}=0$ thì ${\mathrm{v}}_{\mathrm{t}}=\text{ a}.\mathrm{t}$

III. Đồ thị vận tốc -  thời gian của chuyển động thẳng biến đổi đều

Vận tốc tức thời trong chuyển động thẳng biến đổi đều là hàm bậc nhất của thời gian t, nên đồ thị vận tốc thời gian của chuyên động này có hình dạng như sau:

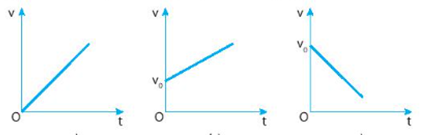
Các dạng đồ thị vận tốc – thời gian trong chuyển động thẳng biến đổi đều

IV. Độ dịch chuyển của chuyển động thẳng biến đổi đều

1. Tính độ dịch chuyển bằng đồ thị vận tốc – thời gian (v - t)

- Trong khoảng thời gian t, nếu vật chuyển động thẳng đều với vận tốc v, thì độ dịch chuyển trong thời gian này có độ lớn $\mathrm{d}=\mathrm{v}.\mathrm{t}$ và có đồ thị (v - t) có dạng như sau  

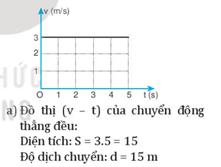
+ Diện tích S = 3. 5 = 15m

+ Độ dịch chuyển d = 15m

- Trong khoảng thời gian t, nếu vật chuyển động thẳng biến đổi đều với vận tốc ban đầu ${\text{v}}_{\mathrm{o}}$, thì công thức tính vận tốc tức thời ${\mathrm{v}}_{\mathrm{t}}={\mathrm{v}}_{\mathrm{o}}+\text{ a}.\mathrm{t}$, đồ thị (v-t) có dạng như sau

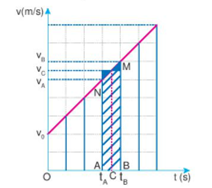
+ Độ lớn độ dịch chuyển trong thời gian t bằng tổng bằng tổng các độ lớn của độ dịch chuyển trong các khoảng thời gian $\mathrm{\Delta t}$, nên có độ lớn bằng diện tích của các hình thang vuông có đường cao là t và có đay là các độ lớn v và ${\text{v}}_{\mathrm{o}}$ 

2. Tính độ dịch chuyển bằng công thức

Độ dịch chuyển trong chuyển động thẳng biến đổi đều là ${\text{d = v}}_{\text{o}}\text{.t + }\frac{\text{1}}{\text{2}}{\text{.a.t}}^{\text{2}}$

Mối liên hệ giữa vận tốc, gia tốc và độ dịch chuyển là ${\text{v}}^{\text{2}}{\text{ - v}}_{\text{o}}^{\text{2}}\text{= 2.a.d}$