Tailieumoi.vn giới thiệu Giải sách bài tập Vật Lí lớp 12 Bài 8: Giao thoa sóng chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Vật Lí 12. Mời các bạn đón xem:
Bài giảng Vật Lí 12 Bài 8: Giao thoa sóng
Giải SBT Vật Lí 12 Bài 8: Giao thoa sóng
Bài 8.1 trang 21 SBT Vật Lí 12: Hai nguồn phát sóng nào dưới đây chắc chắn là hai nguồn kết hợp? Hai nguồn có
A. cùng tần số.
B. cùng biên độ dao động.
C. cùng pha ban đầu.
D. cùng tần số và hiệu số pha không đổi theo thời gian.
Phương pháp giải:
Sử dụng lí thuyết về hai nguồn kết hợp
Lời giải:
Hai nguồn kết hợp có cùng phương, cùng tần số và hiệu số pha không đổi theo thời gian.
Chọn D
Bài 8.2 trang 21 SBT Vật Lí 12: Hai sóng phát ra từ hai nguồn đồng bộ. Cực đại giao thoa nằm tại các điểm có hiệu khoảng cách tới hai nguồn bằng
A. Một bội số của bước sóng.
B. Một ước số nguyên của bước sóng.
C. Một bội số lẻ của nửa bước sóng.
D. Một ước số của nửa bước sóng.
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha:
Lời giải:
Cực đại giao thoa nằm tại các điểm có hiệu khoảng cách tới hai nguồn bằng một bội số của bước sóng.
Chọn A
Bài 8.3 trang 22 SBT Vật Lí 12: Hai nguồn phát sóng đồng bộ nằm sâu trong một bể nước. và là điểm trong bể nước có hiệu khoảng cách tới và bằng một số bán nguyên lần bước sóng. nằm trên đường thẳng ; nằm ngoài đường thẳng đó ( ).
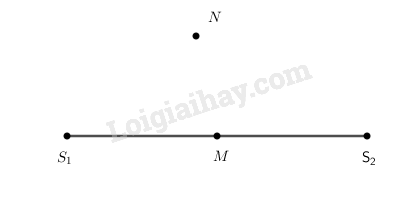
Chọn phát biểu đúng:
A. Các phần tử nước ở và đều đứng yên.
B. Các phần tử nước ở và đều dao động.
C. Các phần tử nước ở dao động, ở đứng yên.
D. Các phần tử nước ở đứng yên, ở dao động.
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha: ; cực tiểu:
Lời giải:
và là điểm trong bể nước có hiệu khoảng cách tới và bằng một số bán nguyên lần bước sóng, thỏa mãn điều kiện cực tiểu
Các phần tử nước tại và đều đứng yên
Chọn A
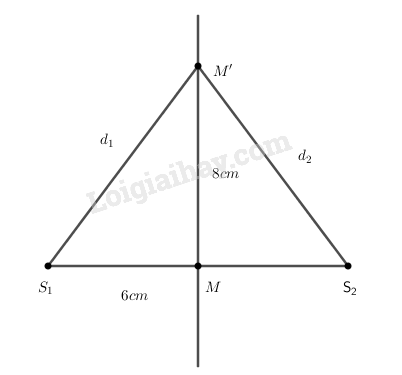
Bài 8.4 trang 22 SBT Vật Lí 12: Ở mặt nước có hai nguồn kết hợp dao động theo phương thẳng đứng với phương trình . Tốc độ truyền sóng là . Coi biên độ sóng không đổi khi sóng truyền đi. Phần tử ở mặt nước cách hai nguồn lần lượt là và có biên độ dao động là
A. B.
C. D.
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha: ; cực tiểu:
Lời giải:
Ta có
Tần số
Bước sóng:
Ta có
tại M là một cực đại
Bài 8.5 trang 22 SBT Vật Lí 12: Hai nguồn sóng trên mặt chất lỏng, cách nhau , dao động cùng pha với tần số . Tốc độ sóng là . Số điểm trên đoạn dao động với biên độ cực đại là
A. B.
C. D.
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha:
Xét:
Số giá trị nguyên là số điểm dao động biên độ cực đại trên
Lời giải:
Bước sóng
Xét:
Có giá trị nguyên Có cực đại trên đoạn
Chú ý: Tại nguồn không thể có cực đại
Chọn A
Bài 8.6 trang 22 SBT Vật Lí 12: Ở bề mặt một chất lỏng có hai nguồn kết hợp và cách nhau . Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là và . Tốc độ truyền sóng trên mặt chất lỏng là . Số điểm dao động với biên độ cực đại trên đoạn thẳng là
A. B.
C. D.
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn ngược pha:
Xét:
Số giá trị nguyên là số điểm dao động biên độ cực đại trên
Lời giải:
Tần số
Bước sóng
Xét:
Có giá trị nguyên Có cực đại trên đoạn
Chú ý: Tại nguồn không thể có cực đại
Chọn C
Bài 8.7 trang 22 SBT Vật Lí 12: Hai điểm S1, S2 trên mặt một chất lỏng, cách nhau 18 cm, dao động cùng pha với biên độ A và tần số f = 20 Hz. Tốc độ truyền sóng trên mặt chất lỏng là v = 1,2 m/s. Hỏi giữa S1, S2 có bao nhiêu gợn sóng (cực đại của giao thoa) hình hypebol ?
Phương pháp giải:
Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha:
Xét:
Số giá trị nguyên là số điểm dao động biên độ cực đại trên
Lời giải:
Bước sóng
Xét:
Có giá trị nguyên Có cực đại trên đoạn
Chú ý: Tại nguồn không thể có cực đại
Vậy, nếu không tính gợn thẳng trùng với đường trung trực của thì có gợn sóng hình hypebol
Bài 8.8 trang 23 SBT Vật Lí 12: Hai mũi nhọn cách nhau , gắn ở đầu một cần rung có tần số , được đặt cho chạm nhẹ vào mặt một chất lỏng. Tốc độ truyền sóng trên mặt chất lỏng là .
a) Gõ nhẹ cần rung thì hai điểm dao động theo phương thẳng đứng với phương trình dạng . Hãy viết phương trình dao động của điểm trên mặt chất lỏng cách đều một khoảng .
b) Dao động của cần rung được duy trì bằng một nam châm điện. Để được một hệ vân giao thoa ổn định trên mặt chất lỏng, phải tăng khoảng cách một đoạn ít nhất bằng bao nhiêu? Với khoảng cách ấy thì giữa hai điểm có bao nhiêu gợn sóng hình hypebol?
Phương pháp giải:
Sử dụng phương trình sóng tổng hợp tại điểm cách nguồn đoạn và cách nguồn đoạn:
Lời giải:
Bước sóng
a) Phương trình sóng tại điểm cách nguồn đoạn d:
b) Khi hệ vân giao thoa đã ổn định thì trung điểm của lại luôn luôn là cực đại giao thoa. Do đó ta phải có:
Ban đầu ta có:
Vậy chỉ cần tăng khoảng cách thêm
Khi đó không tính gợn thẳng trùng với đường trung trực của thì có gợn sóng hình hypebol.
Bài 8.9 trang 23 SBT Vật Lí 12: Một người làm thí nghiệm Hình SGK với một chất lỏng và một cần rung có tần số . Giữa hai điểm người đó đếm được đường hypebol, quỹ tích của các điểm đứng yên. Khoảng cách giữa đỉnh của hai đường hypebol ngoài cùng là . Tính tốc độ truyền sóng.
Phương pháp giải:
Sử dụng biểu thức khoảng cách giữa hai đỉnh hypebol (các điểm đứng yên) gần nhau nhất bằng
Tốc độ truyền sóng
Lời giải:
Giữa đỉnh của hypebol thứ nhất đến hypebol thứ 12 có 11 khoảng
khoảng cách:
Tốc độ truyền sóng
Bài 8.10 trang 23 SBT Vật Lí 12: Dao động tại hai điểm cách nhau trên một mặt chất lỏng có biểu thức: , tốc độ truyền sóng trên mặt chất lỏng là .
a) Giữa hai điểm có bao nhiêu đường hypebol, tại đó chất lỏng dao động mạnh nhất?
b) Viết biểu thức của dao động tại điểm , cách đều một khoảng , và tại điểm nằm trên đường trung trực của và cách đường một khoảng .
Phương pháp giải:
a) Sử dụng điều kiện cực đại giao thoa sóng hai nguồn cùng pha:
Xét:
Số giá trị k nguyên là số điểm dao động biên độ cực đại trên
b) Sử dụng phương trình sóng tổng hợp tại điểm cách nguồn đoạn và cách nguồn đoạn:
Lời giải:
Tần số
Bước sóng:
Xét:
Có giá trị của
Quỹ tích các điểm dao động với biên độ cực đại là đường hypebol
Nếu coi đường trung trực của như một hypebol đặc biệt thì số đường hypebol là
Chú ý: Tại nguồn không thể có cực đại
b) cách đoạn
cách đoạn