Tailieumoi.vn giới thiệu Giải bài tập Vật Lí lớp 12 Bài 8: Giao thoa sóng chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Giao thoa sóng lớp 12.
Bài giảng Vật Lí 12 Bài 8: Giao thoa sóng
Giải bài tập Vật Lí Lớp 12 Bài 8: Giao thoa sóng
Trả lời câu hỏi giữa bài
Trả lời câu C1 trang 42 SGK Vật Lí 12: Những điểm nào trên hình 8.3 SGK biểu diễn chỗ hai sóng gặp nhau triệt tiêu nhau? Tăng cường nhau?
Lời giải:
Trên hình 8.3, các vòng tròn nét liền biểu diễn các gợn lồi, các vòng tròn nét đứt biểu diễn các gợn lõm.
Chỗ gợn lồi gặp gợn lồi hay gợn lõm gặp gợn lõm là những điểm dao động biên độ cực đại (tăng cường nhau).
Chỗ ở đó gợn lồi gặp gợn lõm thì dao động có biên độ cực tiểu (triệt tiêu nhau).
Lời giải:
Công thức (8.2): với
Đúng cho trường hợp vị trí các cực đại giao thoa của hai nguồn dao động cùng pha.
Công thức (8.3):
Đúng cho trường hợp vị trí các cực tiểu giao thoa của hai nguồn dao động cùng pha.
Câu hỏi và bài tập (trang 45 SGK Vật Lí 12)
Bài 1 trang 45 SGK Vật Lí 12: Hiện tượng giao thoa của hai sóng là gì ?
Cực tiểu giao thoa nằm tại các điểm có hiệu đường đi của hai sóng tới đó bằng một số nửa nguyên lần bước sóng
Hiện tượng giao thoa là hiện tượng
A. giao nhau của hai sóng tại một điểm của môi trường.
B. tổng hợp của hai dao động.
C. tạo thành các gợn lồi, lõm.
D. Hai sóng, khi gặp nhau có những điểm chúng luôn tăng cường nhau, có những điểm chúng luôn triệt tiêu nhau.
Ta có: Hiện tượng giao thoa sóng là hiện tượng hai sóng kết hợp khi gặp nhau thì có nhứng điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
=> Đáp án D.
Hai nguồn kết hợp là hai nguồn có
A. cùng biên độ
B. cùng tần số.
C. Cùng pha ban đầu.
D. cùng tần số và hiệu số pha không đổi theo thời gian.
Lời giải:
Ta có: Hai nguồn kết hợp là hai nguồn dao động cùng phương cùng chu kỳ ( hay tần số) và có hiệu số pha không thay đổi theo thời gian.
=> Đáp án D.
Giả sử hai điểm M1 và M2 trên đoạn S1S2 là hai điểm cực đại gần nhau nhất tính từ S1
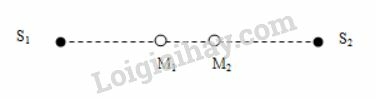
Điểm M1 : (1)
Điểm M2 : (2)
Lấy (2) trừ từng vế cho (1) ta được
Mà có
=> M1M2 = 0,625cm.
* Khoảng cách giữa hai điểm cực đại cạnh nhau trên đoạn S1S2 bằng nửa bước sóng.
+ Áp dụng điều kiện khoảng cách giữa hai điểm đứng yên cạnh nhau trên đoạn S1S2 là
+ Sử dụng biểu thức tính tốc độ truyền sóng:
Lời giải:
Ta có, khoảng cách giữa 2 điểm đứng yên liên tiếp là:
(Khoảng cách giữa n điểm đứng yên liên tiếp
Theo đề bài ta có, 2 điểm và được coi là đứng yên và giữa chúng có điểm đứng yên
=> Trên đoạn có điểm đứng yên (tính cả hai điểm và )
Ta suy ra
Lại có , ta suy ra:
Tốc độ truyền của sóng
Phương pháp giải một số dạng bài tập về giao thoa sóng
Tổng hợp cách giải một số dạng bài tập về giao thoa sóng thường gặp
I. Phương pháp giải bài tập xác định cực đại - Cực tiểu trong giao thoa sóng
1. Dạng 1: Tìm số điểm dao động cực đại - cực tiểu giữa hai nguồn.
Phương pháp
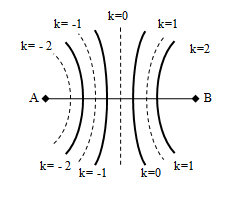
- Hai nguồn cùng pha:
( )
Số Cực đại giữa hai nguồn: và
Số Cực tiểu giữa hai nguồn: và .
hay
- Hai nguồn ngược pha:
Điểm dao động cực đại:
Số đường hoặc số điểm dao động cực đại (không tính hai nguồn):
Số Cực đại:
Hay
Điểm dao động cực tiểu (không dao động):
Số đường hoặc số điểm dao động cực tiểu (không tính hai nguồn):
Số Cực tiểu:
- Hai nguồn vuông pha:
+ Phương trình hai nguồn kết hợp: ;.
+ Phương trình sóng tổng hợp tại M:
+ Độ lệch pha của hai sóng thành phần tại M:
+ Biên độ sóng tổng hợp:
* Số Cực đại:
* Số Cực tiểu: Hay
Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức là đủ
=> Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.
Bài tập ví dụ:
Hai nguồn sóng cơ A,B trên mặt chất lỏng cách nhau 20 cm, dao động theo phương trình: và , Lan truyền trong môi trường với tốc độ v = 1,2 m/s. Tìm số điểm dao động với biên độ cực đại và cực tiểu giữa hai nguồn A và B.
Hướng dẫn giải
Ta có:
Số điểm dao động với biên độ cực đại giữa A,B là:
Vậy có 7 cực đại giữa hai nguồn A,B
Số điểm giao động với biên độ cực tiểu giữa A,B là:
Vậy có 6 cực tiểu giữa hai nguồn A,B.
2. Dạng 2: Số điểm dao động với biên độ cực đại - cực tiểu giữa hai điểm bất kì
Phương pháp:
Số cực đại và cực tiểu trên đoạn thẳng nối hai điểm M và N trong vùng có giao thoa (M gần S1 hơn S2 còn N thì xa S1 hơn S2) là số các giá trị của k tính theo công thức sau ( không tính hai nguồn):
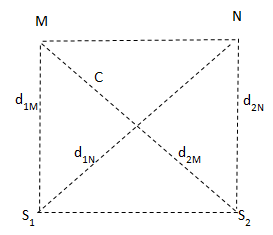
- Dùng công thức:
Số Cực đại:
Số Cực tiểu:
=> Với các nguồn:
+ Hai nguồn dao động cùng pha: ( )
* Số Cực đại:
* Số Cực tiểu:
+ Hai nguồn dao động ngược pha:
* Số Cực đại:
* Số Cực tiểu:
+ Hai nguồn dao động vuông pha:
* Số Cực đại:
* Số Cực tiểu:
Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức
Số giá trị nguyên của k thoả mãn các biểu thức trên là số điểm( đường) cần tìm
3. Dạng 3: Số điểm cực đại, cực tiểu trên đoạn CD tạo với ab một hình vuông hoặc hình chữ nhật.
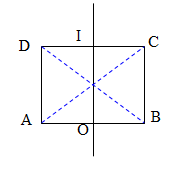
Phương pháp:
Cách 1: Ta tìm số điểm cực đại trên đoạn DI. do DC =2DI, kể cả đường trung trực của CD.
=> Số điểm cực đại trên đoạn DC là:
Đặt : ,
Bước 1: Số điểm cực đại trên đoạn DI thoã mãn :
Với k thuộc Z.
Bước 2 :
Vậy số điểm cực đại trên đoạn CD là :
Số điểm cực tiểu trên đoạn CD :
Cách 2 : Số điểm cực đại trên đoạn CD thoã mãn :
Suy ra :
Hay : .
Giải suy ra k
Số điểm cực tiểu trên đoạn CD thoã mãn :
Suy ra :
Hay : .
Giải suy ra k
Đặt : ,
Tìm Số Điểm Cực Đại Trên Đoạn CD :
Số điểm cực đại trên đoạn CD thoã mãn:
Suy ra :
Hay :
Giải suy ra k
Tìm Số Điểm Cực Tiểu Trên Đoạn CD:
Số điểm cực tiểu trên đoạn CD thoã mãn:
Suy ra :
Hay :
Giải suy ra k
4. Dạng 4: Xác định số điểm cực đại, cực tiểu trên đoạn thẳng là đường chéo của một hình vuông hoặc hình chữ nhật
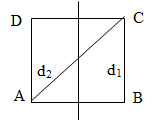
Phương pháp:
Xác định số điểm dao động cực đại trên đoạn CD,
biết ABCD là hình vuông .Giả sử tại C dao động cực đại, ta có:
Số điểm dao động cực đại
5. Dạng 5: Tìm số điểm dao động với biên độ cực đại, cực tiểu tiểu trên đường tròn (hoặc tìm số điểm dao động với biên độ cực đại, cực tiểu trên đường elip, hình chữ nhật, hình vuông, parabol… )
Phương pháp:
Ta tính số điểm cực đại hoặc cực tiểu trên đoạn AB là k. Suy ra số điểm cực đại hoặc cực tiểu trên đường tròn là 2.k . Do mỗi đường cong hypebol cắt đường tròn tại 2 điểm.

6. Dạng 6: Xác định vị trí, khoảng cách của điểm M dao động cực đại, cực tiểu trên đoạn thẳng là đường trung trực của AB , hoặc trên đoạn thẳng vuông góc với hai nguồn A,B.
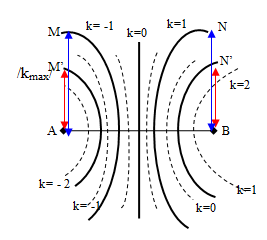
Phương pháp:
Xét 2 nguồn cùng pha ( Xem hình vẽ bên)
Giả sử tại M có dao động với biên độ cực đại.
- Khi thì :
Khoảng cách lớn nhất từ một điểm M đến hai nguồn là : d1=MA
Từ công thức : với , Suy ra được AM
- Khi thì :
Khoảng cách ngắn nhất từ một điểm M’ đến hai nguồn là: d1= M’A
Từ công thức : với , Suy ra được AM’
Lưu ý :
-Với 2 nguồn ngược pha ta làm tương tự.
- Nếu tại M có dao đông với biên độ cực tiểu ta cũng làm tương tự.
II. Phương trình sóng cơ
1. Dạng 1: Xác định phương trình sóng cơ tại một điểm trong trường giao thoa:
Giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S1, S2 cách nhau một khoảng l:
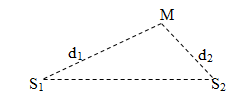
+ Phương trình sóng tại 2 nguồn : (Điểm M cách hai nguồn lần lượt d1, d2)
và
+Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
và
+Phương trình giao thoa sóng tại M:
+Biên độ dao động tại M: với
Bài tập ví dụ:
Tại hai điểm A,B trên mặt nước có hai nguồn dao động theo phương thẳng đứng với phương trình , tốc độ truyền sóng v = 6 m/s. Viết phương trình sóng tại điểm M cách A đoạn 15 cm, các B đoạn 20 cm.
Hướng dẫn giải
Ta có:
Bước sóng:
Phương trình sóng tại M:
2. Dạng 2: Xác định biên độ, ly độ tại một điểm trong miền giao thoa của sóng cơ.
Phương trình sóng tại 2 nguồn: (Điểm M cách hai nguồn lần lượt d1, d2)
và
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
và
- Nếu 2 nguồn cùng pha thì:
và
Phương trình giao tổng hợp sóng tại M:
Thế các số liệu từ đề cho để tính kết quả( giống như tổng hợp dao động nhờ số phức)
- Nếu 2 nguồn cùng biên độ thì:
+ Phương trình sóng tại 2 nguồn :
và
+ Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
và
+ Phương trình giao thoa sóng tại M:
+ Biên độ dao động tại M: với
- TH1: Hai nguồn A, B dao động cùng pha
- TH2: Hai nguồn A, B dao động ngược pha
Ta nhận thấy biên độ giao động tổng hợp là:
- TH3: Hai nguồn A, B dao động vuông pha
Ta nhận thấy biên độ giao động tổng hợp là:
III. Pha dao động tại một điểm trong trường giao thoa
1. Dạng 1: Xác định tại vị trí điểm M dao động cùng pha hoặc ngược pha với nguồn.
Phương pháp
Xét hai nguồn cùng pha:
Cách 1: Dùng phương trình sóng.
Gọi M là điểm dao động ngược pha với nguồn
Phương trình sóng tổng hợp tại M là:
- Nếu M dao động cùng pha với S1, S2 thì:
Suy ra: .Với ta có:
Gọi x là khoảng cách từ M đến AB:
=> Rồi suy ra x
- Nếu M dao động ngược pha với S1, S2 thì:
Suy ra: . Với ta có:
Gọi x là khoảng cách từ M đến AB:
=> Rồi suy ra x
Cách 2: Giải nhanh:
Ta có: (lấy phần nguyên)
- Tìm điểm cùng pha gần nhất: k + 1
- Tìm điểm ngược pha gần nhất: k + 0.5
- Tìm điểm cùng pha thứ n: k + n
- Tìm điểm ngược pha thứ n : k + n - 0.5
Sau đó, ta tính:.
Khoảng cách cần tìm:
2. Dạng 2: Xác định số điểm dao động cùng pha, ngược pha với nguồn trên 1 đoạn thẳng.
Phương pháp
Cách 1: Phương trình sóng tại 2 nguồn cùng biên độ A:(Điểm M cách hai nguồn lần lượt d1, d2)
và
+Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
và
+Phương trình giao thoa sóng tại M:
Pha ban đầu sóng tại M :
Pha ban đầu sóng tại nguồn S1 hay S2 : hay
Độ lệch pha giữa 2 điểm M và nguồn S1 (hay S2 )
Để điểm M dao động cùng pha với nguồn 1:
=>
Để điểm M dao động ngược pha với nguồn 1:
=>
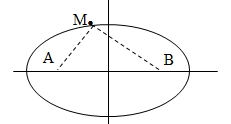
Tập hợp những điểm dao động cùng pha với 2 nguồn là họ đường Ellip nhận S1 và S2 làm 2 tiêu điểm.
Tập hợp những điểm dao động ngược pha với 2 nguồn là họ đường Ellip nhận S1 và S2 làm 2 tiêu điểm xen kẻ với họ đường Ellip trên
Cách 2: Phương pháp nhanh :
Xác định số điểm cùng pha, ngược pha với nguồn S1S2 giữa 2 điểm MN trên đường trung trực
Ta có:
;
- Cùng pha khi: ;
- Ngược pha khi: ;
Từ k và kM => số điểm trên OM
Từ k và kN => số điểm trên ON
=> số điểm trên MN ( cùng phía thì trừ, khác phía thì cộng)
Lý thuyết Bài 8: Giao thoa sóng
I. Giao thoa sóng - Lí thuyết chung
1. Hiện tượng giao thoa
- Khi sóng mặt nước gặp một khe chắn hẹp có kích thước nhỏ hơn bước sóng thì sóng truyền qua khe giống như một tâm phát sóng mới.
- Hai nguồn kết hợp là hai nguồn dao động cùng phương, cùng chu kì (hay tần số) và có hiệu số pha không đổi theo thời gian. Hai nguồn kết hợp có cùng pha là hai nguồn đồng bộ.
- Hai sóng do hai nguồn kết hợp phát ra là hai sóng kết hợp.
Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa.
2. Cực đại và cực tiểu
- Giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S1, S2 cách nhau một khoảng l:
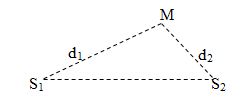
và
và
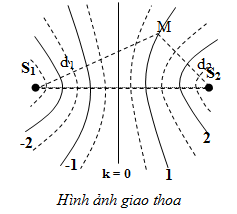
+ Khoảng cách giữa 1 cực đại và 1 cực tiểu gần nhất là
+ Tại I trung điểm của 2 nguồn sóng:
3. Điều kiện giao thoa - Sóng kết hợp
Hai sóng là hai sóng kết hợp tức là hai sóng cùng tần số và có độ lệch pha không đổi theo thời gian (hoặc hai sóng cùng pha).
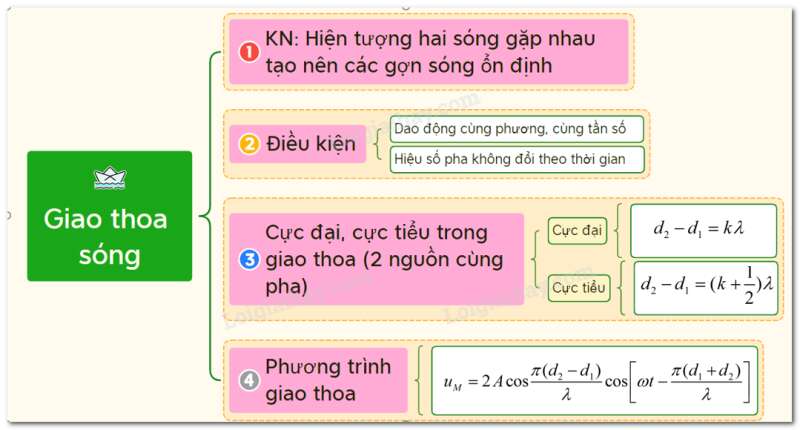
II. Sơ đồ tư duy về giao thoa sóng