Với tóm tắt lý thuyết Toán lớp 3 Bài 16: Điểm ở giữa, trung điểm của đoạn thẳng sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc, có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 3.
Lý thuyết Toán lớp 3 Bài 16: Điểm ở giữa, trung điểm của đoạn thẳng
A. Lý thuyết Điểm ở giữa, trung điểm của đoạn thẳng
a) Điểm ở giữa
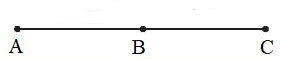

b) Trung điểm của đoạn thẳng
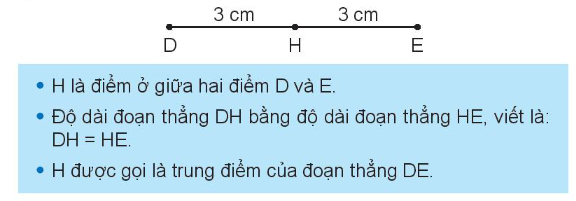
B. Bài tập trắc nghiệm Điểm ở giữa, trung điểm của đoạn thẳng
Câu 1: Điểm M là trung điểm của đoạn thẳng YZ.
Hình nào dưới đây vẽ đúng ?
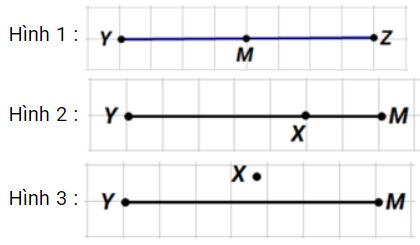
A. Hình 1
B. Hình 2
C. Hình 3
Đáp án: A
Giải thích:
Ta có: M là trung điểm nên điểm M nằm giữa hai điểm Y và Z, độ dài đoạn ZM = MY nên hình vẽ đúng là hình 1.
Câu 2: Cho hình vẽ sau: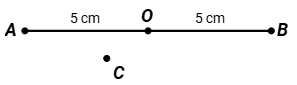
Khẳng định nào dưới đây là đúng ?
A. Điểm C là trung điểm của đoạn thẳng AB.
B. Điểm C ở giữa hai điểm A và O.
C. Điểm O là trung điểm của đoạn thẳng AB.
D. Điểm bốn điểm A, C, O, B thẳng hàng.
Đáp án: C
Giải thích:
Quan sát hình ta thấy bốn điểm A, C, O, B không thẳng hàng.
Điểm O ở giữa hai điểm A và B; AO = OB nên điểm O là trung điểm của đoạn thẳng AB.
Câu 3: Cho hình vẽ như bên dưới: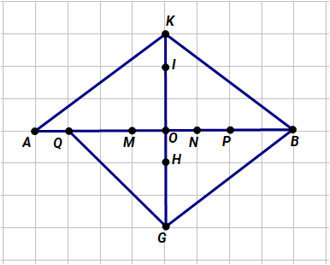
Có bao nhiêu đoạn thẳng trong hình nhận điểm O là trung điểm?
A. 1 đoạn thẳng
B. 2 đoạn thẳng
C. 3 đoạn thẳng
D. 4 đoạn thẳng
Đáp án: C
Giải thích:
Quan sát hình ta thấy các đoạn thẳng MN, AB, KG nhận điểm O là trung điểm vì điểm O nằm giữa các cặp điểm M, N; A, B; K, G và OM = ON, OA = OB, OK = OG.
Vì vậy có 3 đoạn thẳng nhận điểm O là trung điểm.
Câu 4: Cho hình vẽ dưới đây: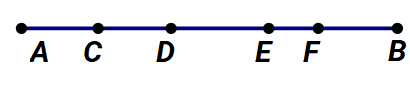
Trong hình vẽ đã cho, những điểm ở giữa hai điểm A và F là:
A. Ba điểm C, D, E.
B. Ba điểm D, E, B.
C. Ba điểm C, E, B.
D. Ba điểm A, C, F.
Đáp án: A
Giải thích:
Quan sát hình ta thấy, các điểm A, B, C, D, E, F cùng nằm trên một đường thẳng.
Có ba điểm D, C, E ở giữa hai điểm A và F.
Câu 5: Hình vẽ sau có bao nhiêu điểm ở giữa hai điểm khác ?
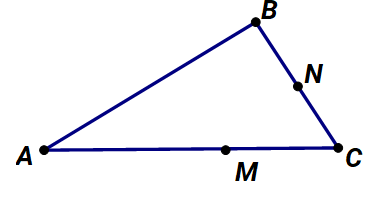
A. 0 điểm
B. 1 điểm
C. 2 điểm
D. 3 điểm
Đáp án: C
Giải thích:
Quan sát hình ta thấy:
Ba điểm A, M, C là ba điểm thẳng hàng và điểm M ở giữa hai điểm A và C.
Ba điểm B, N, C là ba điểm thẳng hàng và điểm N ở giữa hai điểm B và C.
Vậy ta có hai điểm ờ giữa hai điểm khác là: điểm M ở giữa hai điểm A và C, điểm N ở giữa hai điểm B và C.
Câu 6: Hình vẽ nào dưới đây mà điểm A không là điểm ở giữa hai điểm B và C?
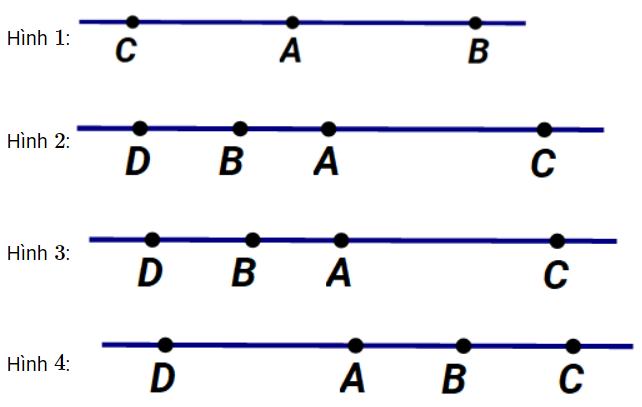
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Đáp án: D
Giải thích:
Quan sát hình vẽ, ta thấy các điểm trên mỗi hình đều cùng nằm trên một đường thẳng nên chúng thẳng hàng, tuy nhiên chỉ có hình 4 là điểm A không nằm giữa B và C.
Câu 7: Cho hình vẽ:
Ba điểm nào sau đây là ba điểm thẳng hàng?
A. A, O, C
B. A, O, B
C. A, O, D
D. C, O, B
Đáp án: B
Giải thích:
Quan sát hình ta thấy, trên hình có hai đường thẳng.
A, O, B cùng nằm trên một đường thẳng nên là ba điểm thẳng hàng.
C, O, D cùng nằm trên một đường thẳng nên là ba điểm thẳng hàng.
Còn A, O, C không cùng nằm trên một đường thẳng; A, O, D không cùng nằm trên một đường thẳng; C, O, B không cùng nằm trên một đường thẳng nên không thẳng hàng.
Câu 8: Trung điểm của đoạn thẳng DE là điểm nào?
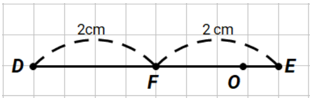
A. Điểm F
B. Điểm E
C. Điểm O
D. Điểm D
Đáp án: A
Giải thích:
Quan sát hình ta thấy điểm F ở giữa hai điểm D và E; DF = FE nên điểm F là trung điểm của đoạn thẳng DE.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 3 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 14: Một phần mấy
Lý thuyết Bài 16: Điểm ở giữa, trung điểm của đoạn thẳng
Lý thuyết Bài 17: Hình tròn. Tâm, bán kính, đường kính của hình tròn
Lý thuyết Bài 18: Góc, Góc vuông, góc không vuông
Lý thuyết Bài 19: Hình tam giác, hình tứ giác. Hình chữ nhật, hình vuông
Bài giảng Toán lớp 3 trang 50, 51 Bài 13: Điểm ở giữa, trung điểm của đoạn thẳng - Kết nối tri thức