Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Dạng toán về Khi nào thì AM+MB=AB Toán lớp 6, tài liệu bao gồm 5 trang, tuyển chọn bài tập Dạng toán về khi nào thì AM+MB=AB đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Dạng toán về Khi nào thì AM+MB=AB gồm các nội dung chính sau:

A. Phương phương giải

- tóm tắt lý thuyết ngắn gọn.

B. Các dạng bài tập và phương pháp giải

- gồm 2 dạng bài tập minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.

C. Bài tập tự luyện

- gồm 5 bài tập tự luyện có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các Dạng toán về Khi nào thì AM+MB=AB.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

KHI NÀO THÌ AM+MB=AB?

A. Phương pháp giải

1. Khi nào thì tổng độ dài hai đoạn thẳng AM và MB bằng độ dài đoạn thẳng AB?

Nếu điểm M nằm giữa hai điểm A và B thì AB = AM + MB. Ngược lại, nếu AB = AM + MB thì điểm M nằm giữa hai điểm A và B.

Ví dụ: Cho điểm M nằm giữa hai điểm A và B. Biết , tính độ dài đoạn thẳng MB?

Giải: Vì điểm M nằm giữa A và B thì AB = AM + MB.

Thay AM = 3cm, AB = 8cm, ta được: 3 + MB = 8 ⇒ MB = 8 - 3 = 5(cm)

2. Một vài dụng cụ đo khoảng cách giữa hai điểm trên mặt đất

Muốn đo khoảng cách giữa hai điểm trên mặt đất, trước hết ta phải gióng một đường thẳng đi qua hai điểm đó rồi dùng thước cuộn bằng vải hoặc thước cuộn bằng kim loại.

   + Nếu khoảng cách giữa hai điểm trên mặt đất nhỏ hơn độ dài thước cuộn thì chỉ cần giữ cố định một đầu thước tại một điểm rồi căng thước đi qua điểm thứ hai.

   + Nếu khoảng cách giữa hai điểm trên mặt đất lớn hơn độ dài thước cuộn thì sử dụng liên tiếp thước cuộn nhiều lần

   + Đôi khi người ta dùng thức chữ A có khoảng cách giữa hai chân là 1m hoặc 2m

B. Các dạng bài tập và phương pháp giải

Ví dụ 1: Cho điểm M nằm giữa hai điểm A và B. Biết AB=6cm, AM=2cm. Tính độ dài BM

Lời giải:

M nằm giữa A và B, ta có:

$\begin{array}{l}AM+MB=AB\\ 2+MB=6\\ MB=4\left(cm\right)\end{array}$

Ví dụ 2: Cho điểm I nằm giữa C và D. Biết rằng $IC-ID=1cm$ và CD=5cm. Tính độ dài IC và ID

Lời giải:

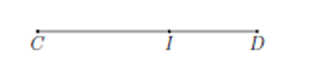
I nằm giữa C và D. ta có: $\begin{array}{l}IC+ID=CD\\ IC+ID=5\end{array}$

Mà $IC-ID=1$

Do đó $\begin{array}{l}IC=(5+1):2=3\left(cm\right)\\ ID=(5-1):2=2\left(cm\right)\end{array}$

Dạng 2: Xác định điểm nằm giữa hai điểm khác

Ví dụ 3: Cho ba điểm A, B, C, biết AC=2cm, BC=3cm, AB=5cm. Điểm nào nằm giữa hai điểm còn lại?

Lời giải:

Ta có: AC+BC=2cm+3cm=5cm

Suy ra: AC+BC=AB

Do đó điểm C nằm giữa A và B

Nhận xét: Bạn nên thực hiện tổng hai số đo đoạn thẳng nhỏ AC, BC sau đó so sánh kết quả với số đo đoạn lớn nhất AB. Nếu bằng nhau thì điểm C nằm giữa hai điểm A và B.

Ví dụ 4: Cho ba điểm A, B, C biết AB=3,1cm; AC=1,9cm; BC=4cm.

1.     Chứng tỏ trong ba điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại.

2.     Chứng tỏ rằng ba điểm A, B, C không thẳng hàng