Viết phương trình tiếp tuyến của hypebol
a) Tại điểm ;
b) Tại điểm có hoành độ bằng -1;
c) Biết rằng hệ số góc của tiếp tuyến bằng
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: Với mọi x0 ≠ 0:
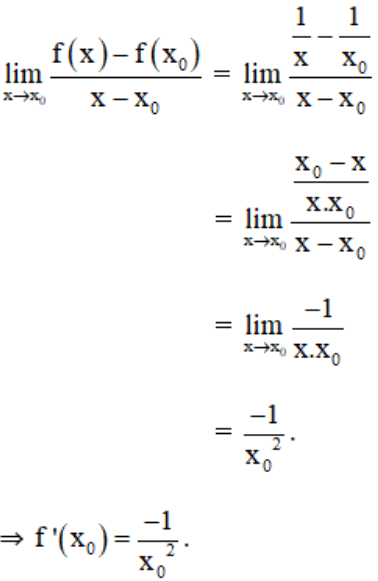
b) Tại x0 = -1
⇒ y0 = -1
⇒ f’(x0) = -1.
Vậy phương trình tiếp tuyến của đường cong 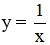
y = -1(x + 1) – 1 = -x – 2.
⇒ Phương trình tiếp tuyến:
Vậy có hai phương trình tiếp tuyến của hypebol 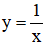
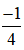
Một vật rơi tự do theo phương trình , trong đó là gia tốc trọng trường.
a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến, trong các trường hợp ; ; .
b. Tìm vận tốc tức thời của chuyển động tại thời điểm .
Viết phương trình tiếp tuyến đường cong .
a. Tại điểm ;
b. Tại điểm có hoành độ bằng 2;
c. Biết hệ số góc của tiếp tuyến bằng 3.
Bằng định nghĩa, hãy tính đạo hàm của các hàm số:
a) tại điểm x bất kì;
b) tại điểm bất kì
Tính ( bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: tại
Chứng minh rằng hàm số:
Không có đạo hàm tại điểm nhưng có đạo hàm tại điểm .
a) Vẽ đồ thị của hàm số .
b) Tính f’(1).
c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.
Một đoàn tàu chuyển động khởi hành từ một nhà ga. Quãng đường s (mét) đi được của đoàn tàu là một hàm số của thời gian t (phút). Ở những phút đầu tiên, hàm số đó là .
Hãy tính vận tốc trung bình của chuyển động trong khoảng với và .
Nêu nhận xét về những kết quả thu được khi t càng gần .