Trên đường tròn lượng giác gốc A, lấy điểm M sao cho góc lượng giác (OA, OM) = . Gọi M1 là điểm đối xứng với M qua Ox. Số đo của các góc lượng giác (OA, OM1) là:
A. + k2π, k ∈ ℤ;
B. + k2π, k ∈ ℤ;
C. + k2π, k ∈ ℤ;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
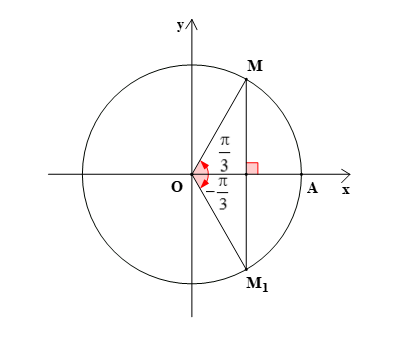
Vì M1 là điểm đối xứng của M qua trục Ox với góc lượng giác (OA, OM) = nên góc lượng giác (OA, OM1) được tạo bởi tia đầu là tia OA, tia cuối là tia OM1 và
+ quay theo chiều dương một góc bằng và chỉ có duy nhất một điểm M1 trên đường tròn lượng giác (do M1 đối xứng với M qua Ox) nên có số đo của các góc lượng giác (OA, OM1) = + k2π, k ∈ ℤ.
+ quay theo chiều âm một góc và chỉ có duy nhất một điểm M1 trên đường tròn lượng giác (do M1 đối xứng với M qua Ox) nên có số đo của các góc lượng giác (OA, OM1) = + k2π, k ∈ ℤ.
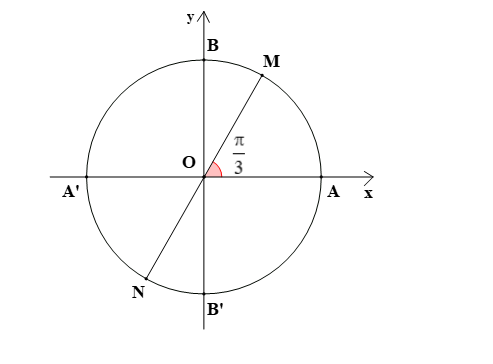
Trên hình vẽ, hai điểm M, N biểu diễn các góc lượng giác có số đo là:
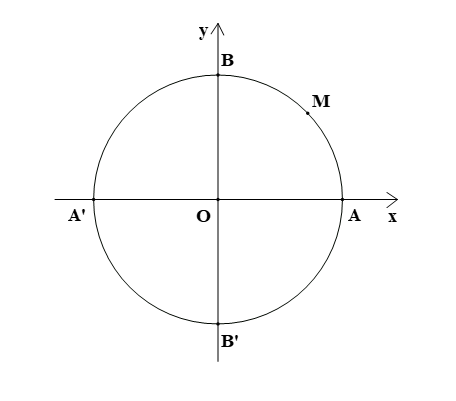
Điểm biểu diễn góc lượng giác có số đo bằng là điểm nào trong hình vẽ dưới đây?
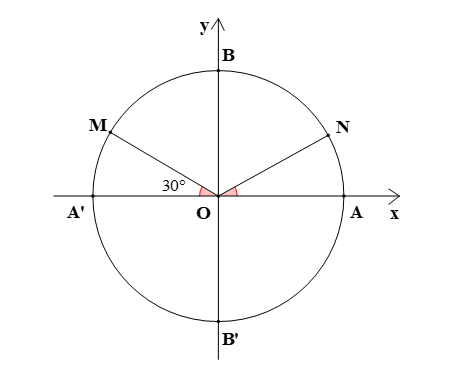
Trên đường tròn với điểm gốc là A. Điểm M thuộc đường tròn sao cho Gọi N là điểm đối xứng với M qua trục Oy, số đo của các góc lượng giác (OA, ON) là
Khi biểu diễn góc lượng giác trên đường tròn lượng giác, khẳng định nào sau đây là sai?
Điểm biểu diễn góc lượng giác có số đo bằng là điểm nào trong hình vẽ dưới đây?
Số điểm M trên đường tròn lượng giác biểu diễn các góc lượng giác có số đo bằng , k ∈ ℤ là