Tính thể tích của khối chóp cụt lục giác đều ABCDEF.A′B′C′D′E′F′ với O và O′ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và .
 Giải bởi Vietjack
Giải bởi Vietjack

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có O là giao điểm của hai đường chéo, . Tính khoảng cách từ O đến mặt phẳng (SCD).
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng AC và SB.
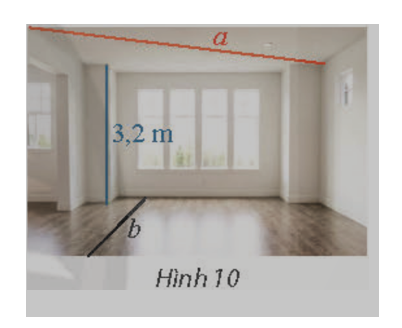
Một căn phòng có trần cao 3,2 m. Tính khoảng cách giữa một đường thẳng a trên trần nhà và đường thẳng b trên sàn nhà.
Cho hình hộp đứng ABCD.A′B′C′D′ có cạnh bên AA′ = 2a và đáy ABCD là hình thoi có AB = a và .
a) Tính khoảng cách giữa hai đường thẳng BD và AA′.
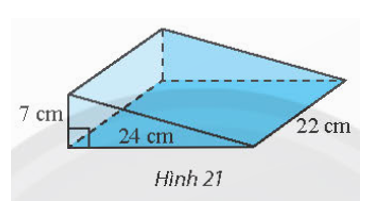
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.
Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng AB ⊥ CD.
Cho tứ diện OABC có ba cạnh OA, OB, OC đều bằng a và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng:
a) OA và BC;
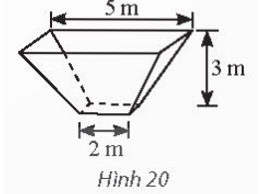
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.
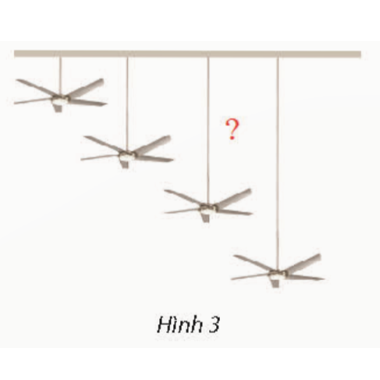
Một quạt trần có bề dày thân quạt bằng 20 cm. Người ta muốn treo quạt sao cho khoảng cách từ quạt đến sàn nhà là 2,5 m. Hỏi phải làm cán quạt dài bao nhiêu? Cho biết trần nhà cao 3,6 m.
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa b và song song với a. Gọi (P) là mặt phẳng chứa đường thẳng a, vuông góc với (Q) và cắt b tại J. Trong (P), gọi c là đường thẳng đi qua J vuông góc với a và cắt a tại điểm I.

Đường thẳng IJ có vuông góc với b không? Giải thích.
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách :
a) Giữa hai mặt phẳng (ACD′) và (A′C′B) ;