Tìm GTLN và GTNN của hàm số sau y= (sinx + 2cosx + 1)/(sinx + cosx +2)...

Question

Tìm GTLN và GTNN của hàm số sau: y=sinx + 2cosx + 1sinx + cosx +2

VietJack · Accepted Answer

Chọn B Ta có: sin x+ cosx = 2sin(x + π4)- 1≤sin (x + π4)≤ 1⇔-2≤2.sin (x + π4)≤2⇒2.sin (x + π4) + 2 > 0 hay sinx + cosx + 2 > 0 với mọi x. Phương pháp giải Để tìm được giá trị lớn nhất;giá trị nhỏ nhất của hàm số ta cần chú ý: + Với mọi x ta luôn có: - 1 ≤ cosx ≤ 1; -1 ≤ sinx ≤ 1 +Với mọi x ta có: 0 ≤ |cosx| ≤ 1 ;0 ≤ |sinx| ≤ 1 + Bất đẳng thức bunhia –copski: Cho hai bộ số (a1; a2) và (b1;b2) khi đó ta có: (a1.b1+ a2.b2 )2 ≤ ( a12+ a22 ).( b12+ b22 ) Dấu “=” xảy ra khi: a1/a2 = b1/b2 + Giả sử hàm số y= f(x) có giá trị lớn nhất là M và giá trị nhỏ nhất là m. Khi đó; tập giá trị của hàm số là [m; M]. + Phương trình : a. sinx+ b. cosx= c có nghiệm khi và chỉ khi a2 + b2 ≥ c2 Dạng 1. Sử dụng tính bị chặn của hàm số lượng giác Phương pháp giải: -1 ≤ sin [u(x)] ≤ 1; 0 ≤ sin2[u(x)] ≤ 1; 0 ≤ |sin[u(x)]| ≤ 1 -1 ≤ cos [u(x)] ≤ 1; 0 ≤ cos2[u(x)] ≤ 1; 0 ≤ |cos[u(x)]| ≤ 1 Dạng 2. 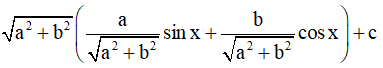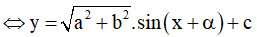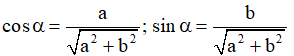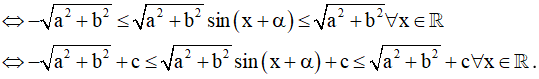Hàm số có dạng y = asinx + bcosx + c (với a, b khác 0) Phương pháp giải: Bước 1: Ta đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]: y = asinx + bcosx + c = với α thỏa mãn Bước 2: Đánh giá -1 ≤ sin (x + α) ≤ 1 ∀x ∈ R Dạng 3: Hàm số có dạng 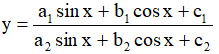Lý thuyết: Phương trình asinx + bcosx = c có nghiệm khi a2 + b2 ≥ c2 (Lý thuyết có trong phần 7) Phương pháp giải: Bước 1: Điều kiện xác định: a2sinx + b2cosx = c2 ≠ 0 Bước 2: 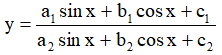⇔ ya2sinx + yb2cosx + yc2 = a1sinx + b1cosx + c1 ⇔ (ya2 - a1)sinx + (yb2 - b1)cosx = -yc + c1 (*) Bước 3: Để phương trình (*) có nghiệm x thì (ya2 - a1)2 + (yb2 - b1)2 ≥ (-yc + c1)2 Tìm đoạn chứa y, sau đó đưa ra kết luận về giá trị lớn nhất và giá trị nhỏ nhất. Bài tập liên quan: Tìm nghiệm lớn nhất của phương trình: sin3x-23sin2x =2sinxcos2x thuộc đoạn 0;2π? Cách giải: Tham khảo thêm một số tài liệu liên quan: Chuyên đề Hàm số lượng giác và phương trình lượng giác 172 bài tập trắc nghiệm hàm số lượng giác và phương trình lượng giác

Câu hỏi:

Tìm GTLN và GTNN của hàm số sau: $y = \frac{\sin x + 2 \cos x + 1}{\sin x + \cos x + 2}$

A. min y = 0, max y = 1

B. min y= -2, max y= 1

C. min y =-1, max y= 1

D. Tất cả sai

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tập xác định của hàm số $y = \tan x + c o t x$ là

Câu 2:

Tìm GTLN và GTNN của hàm số
y=3sinx + 4cosx + 5

Câu 3:

Trong các hàm số sau hàm số nào là hàm số chẵn

Câu 4:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: $y = 2 \sin^{2} x + \cos^{2} 2 x$

Câu 5:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=4sinxcosx +1

Câu 6:

Tìm GTLN và GTNN của hàm số sau: $y = 1 - \sqrt{2 \cos^{2} x + 1}$

Câu 7:

Hàm số $y = \sqrt{3} + 2 \cos x$ tăng trên khoảng:

Câu 8:

Tìm tập xác định của hàm số sau: $y = \tan (x - \frac{π}{6})$

Câu 9:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 4 - 3 \sin^{2} 2 x$

Câu 10:

Tìm tất cả các nghiệm của phương trình sin x + sin 2x + sin3x = 0 thuộc $(0; π)$

Câu 11:

Hàm số nào sau đây là hàm số chẵn

Câu 12:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhât của hàm số sau: $y = 1 + 3 \sin (2 x - \frac{π}{4})$

Câu 13:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: $y = 3 - 2 \cos^{2} 3 x$

Câu 14:

Tìm GTLN và GTNN của hàm sau: $y = \sqrt{2 \sin x + 3}$

Đề thi liên quan

Câu hỏi mới nhất