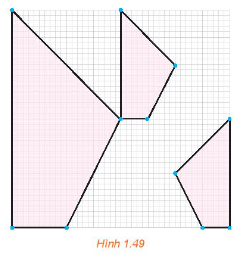
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
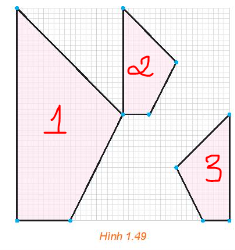
Hình nhỏ 2 là ảnh của hình lớn qua một phép vị tự.


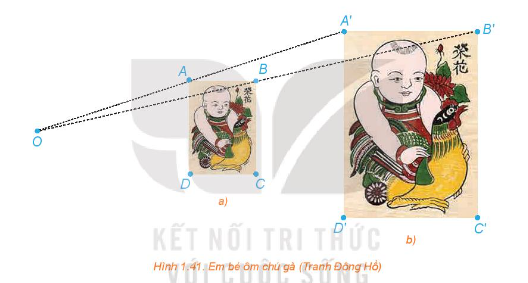
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\).
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Cho phép vị tự tâm O, tỉ số k biến điểm M thành điểm M'¸điểm N thành điểm N'.
a) Biểu diễn các vectơ \(\overrightarrow {OM'} ,\,\overrightarrow {ON'} \) tương ứng theo các vectơ \(\overrightarrow {OM} ,\,\overrightarrow {ON} \).
b) Giải thích vì sao \(\overrightarrow {M'N'} = k\overrightarrow {MN} \).
Trong mặt phẳng tọa độ Oxy, cho A(1; 2), B(3; 6). Viết phương trình đường tròn (C) là ảnh của đường tròn đường kính AB qua phép vị tự V(O, 3).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)2 + (y – 2)2 = 25.
a) Tìm tâm I và bán kính R của đường tròn (C).
b) Tìm tâm I' và bán kính R' của đường tròn (C') là ảnh của đường tròn (C) qua phép vị tự tâm A(3; 5), tỉ số 2.
c) Viết phương trình của (C').