Hãy thực hiện các phép tính sau trong hệ nhị phân:
a) 101101 + 11001
b) 100111 × 1011
 Giải bởi Vietjack
Giải bởi Vietjack
a) 101101 + 11001 = 1000110
b) 100111 × 1011 = 110101101
Các phép tính số học trong nhị phân
a) Bảng cộng và nhân trong hệ nhị phân
- Phép cộng và nhân tương tự trong hệ thập phân
|
x |
y |
x + y |
x × y |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
10 |
1 |
Bảng 1: Bảng cộng và nhân trong hệ nhị phân
b) Cộng hai số nhị phân
- Khi phép cộng hai bit có kết quả là 10 thì ghi 0 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng bên trái. Có thể xảy ra trường hợp cộng 2 bit 1 mà phải nhớ từ hàng trước chuyển sang thì kết quả sẽ là 11, khi đó ta ghi 1 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng tiếp theo bên trái.
Ví dụ: Phép cộng hai số nhị phân 11011 và 11010.
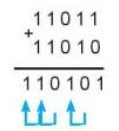
Hình 1.2: Thực hiện phép cộng
c) Nhân hai số nhị phân
Nhân thừa số thứ nhất lần lượt với từng chữ số của thừa số thứ hai, theo thứ tự từ phải sang trái và đặt kết quả căn phải theo đúng vị trí chữ số của thừa số thứ hai, rồi cộng tất cả lại.
Ví dụ: Phép nhân 1101 với 101 trong hệ nhị phân.
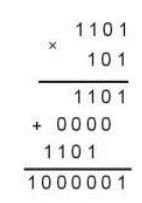
Hình 1.3: Thực hiện phép nhân
Xem thêm một số kiến thức liên quan:
20 câu Trắc nghiệm Tin học 10 Bài 4 (Kết nối tri thức) có đáp án: Hệ nhị phân và dữ liệu số nguyên
Lý thuyết Tin học 10 Bài 4 (Kết nối tri thức): Hệ nhị phân và dữ liệu số nguyên
Em hãy đổi các số sau từ hệ nhị phân sang hệ thập phân.
a)110011
b) 10011011
c) 1001110
Em hãy đổi các số sau từ hệ thập phân sang hệ nhị phân.
a) 13
b) 155
c) 76
Em hãy tìm hiểu mã bù 2 với hai nội dung:
a) Mã bù 2 được lập như thế nào?
b) Mã bù 2 được dùng để làm gì?Hãy thực hiện các phép tính sau đây theo quy trình Hình 4.4.
a) 125 + 17
b) 250 + 175
c) 75 + 112
Phép tính trong hệ nhị phân
Hãy chuyển các toán hạng của hai phép tính sau ra hệ nhị phân để chuẩn bị kiểm tra kết quả thực hiện các phép toán trong hệ nhị phân. (Ví dụ 3 + 4 = 7 sẽ được chuyển hạng thành 11 + 100 = 111).
a) 26 + 27 = 53
b) 5 × 7 = 35
Em hãy thực hiện phép tính sau đây theo quy trình Hình 4.4
a) 15 × 6
b) 11 × 9
c) 125 × 4
Trong hệ thập phân, mỗi số có thể được phân tích thành tổng các luỹ thừa của 10 với hệ số của mỗi số hạng chính là các chữ số tương ứng của số đó. Ví dụ số 513 có thể viết thành:
Ta cũng có thể phân tích một số thành tổng các luỹ thừa của 2, chẳng hạn 13 có thể viết thành: với các hệ số chỉ là 0 hoặc 1
Khi đó, có thể thể hiện 13 bởi 1101 được không? Em hãy cho biết việc thể hiện giá trị của một số bằng dãy bit có lợi gì.
Biểu diễn một số dưới dạng tổng luỹ thừa của 2
Em hãy viết số 19 thành một tổng các luỹ thừa của 2.
Gợi ý: hãy lập danh sách các luỹ thừa của 2 như 16, 8, 4, 2, 1 và tách dần khỏi 19 cho đến hết.