Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O. Hãy so sánh các vectơ và , và .
 Giải bởi Vietjack
Giải bởi Vietjack
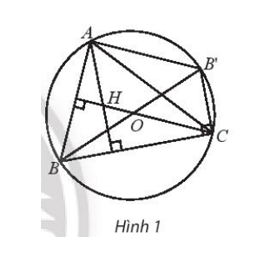
Do BB’ là đường kính nên = 90° ( góc nội tiếp chắn nửa đường tròn )
⇒ BC ⊥ B’C.
H là trực tâm tam giác ABC nên BC ⊥ AH.
Suy ra AH // B’C ( do đều vuông góc với BC ).
Do BB’ là đường kính nên = 90° ( góc nội tiếp chắn nửa đường tròn )
⇒ BA ⊥ B’A.
H là trực tâm tam giác ABC nên CH ⊥ BA.
Suy ra CH // B’A ( do đều vuông góc với BA ).
Như vậy AB’CH là hình bình hành ( DHNB hình bình hành )
⇒ = và = .
Vậy = và = .
Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Cho hai điểm phân biệt A và B. Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:
A. IA = IB;
B. ;
C. ;
D. .
Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ có điểm đầu và điểm cuối là các đỉnh của lục giác là:
A. 2;
B. 3;
C. 4;
D. 6.
Cho ba điểm A, B, C. Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Cho hình chữ nhật ABCD có AB = 3, BC = 4. Độ dài của vectơ là:
A. 5;
B. 6;
C. 7;
D. 9.
Cho tam giác ABC vuông ở A và có = 50°. Khẳng định nào sau đây là sai?
A. = 130°;
B. = 40°;
C. = 50°;
D. = 120°.
Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai?
A. ;
B. ;
C. ;
D. .
Cho ngũ giác ABCDE. Gọi M, N, P, Q, R lần lượt là trung điểm các cạnh AB, BC, CD, DE, EA. Chứng minh hai tam giác EMP và NQR có cùng trọng tâm.
Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ và :
a) cùng hướng?
Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC. Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Cho tam giác ABC, O là điểm sao cho ba vectơ , , có độ dài bằng nhau và + + = . Tính các góc , , .
Cho và là hai vectơ cùng hướng và đều khác vectơ . Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .