Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:
a) ;
b) .
Giải bởi Vietjack
a) Vì P và N lần lượt là trung điểm của AB và AC nên PN là đường trung bình của tam giác ABC.
Do đó: PN // = BC.
Khi đó hai vectơ và cùng hướng và PN = BC.
Suy ra: .
Do đó: .
Vậy .
b) M và P lần lượt là trung điểm của BC và AB nên MP là đường trung bình của tam giác ABC.
Do đó: MP // = AC.
Lại có hai vectơ và cùng hướng và MP = CA nên .
Hay .
Khi đó ta có: .
Vậy .
Phương pháp giải
1. Định nghĩa
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Tam giác ABC có D, E lần lượt là trung điểm của AB, AC. Khi đó, DE là đường trung bình của tam giác ABC.
2. Định lí
• Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Tam giác ABC có D là trung điểm của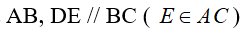 
. Khi đó, E là trung điểm của AC.
• Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh.
Tam giác ABC có DE là đường trung bình. Khi đó: 
Xem thêm kiến thức liên quan
Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm của tam giác BCD. Chứng minh:
a) ;
b) ;
c) Điểm G thuộc đoạn thẳng AE và .
Cho tam giác ABC. Các điểm D, E, H thỏa mãn .
a) Biểu thị mỗi vectơ theo hai vectơ .
b) Chứng minh D, E, H thẳng hàng.
Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G. Tìm các số a, b biết: .
Cho G là trọng tâm của tam giác ABC và điểm M tùy ý. Chứng minh rằng .
Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ .
Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử , . Biểu diễn các vectơ theo .
Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
Cho đoạn thẳng AB = 6 cm.
a) Xác định điểm C thỏa mãn .
b) Xác định điểm D thỏa mãn .
Cho I là trung điểm của đoạn thẳng AB và điểm M tùy ý. Chứng minh rằng .
Hai đoàn tàu chạy song song (Hình 58). Gọi lần lượt là các vectơ mô tả vận tốc của hai đoàn tàu.
Mối liên hệ giữa hai vectơ vận tốc là như thế nào?
Cho hai vectơ và khác sao cho với k là số thực khác 0. Nêu nhận xét về phương của hai vectơ và .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
