Cho tam giác ABC có AB = 6, AC = 8 và .
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
Các công thức tính diện tích tam giác:
(1) S = aha = bhb = chc
(2) S = ab.sinC = bc.sinA = ac.sinB;
(3) S = ;
(4) S = pr;
(5) (Công thức Heron).
Hướng dẫn giải:
a) Áp dụng công thức tính diện tích tam giác ta có:
Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).
b) Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA = 62 + 82 – 2.6.8.cos60° = 52
⇒ BC = ≈ 7,2.
Mặt khác diện tích tam giác ABC:
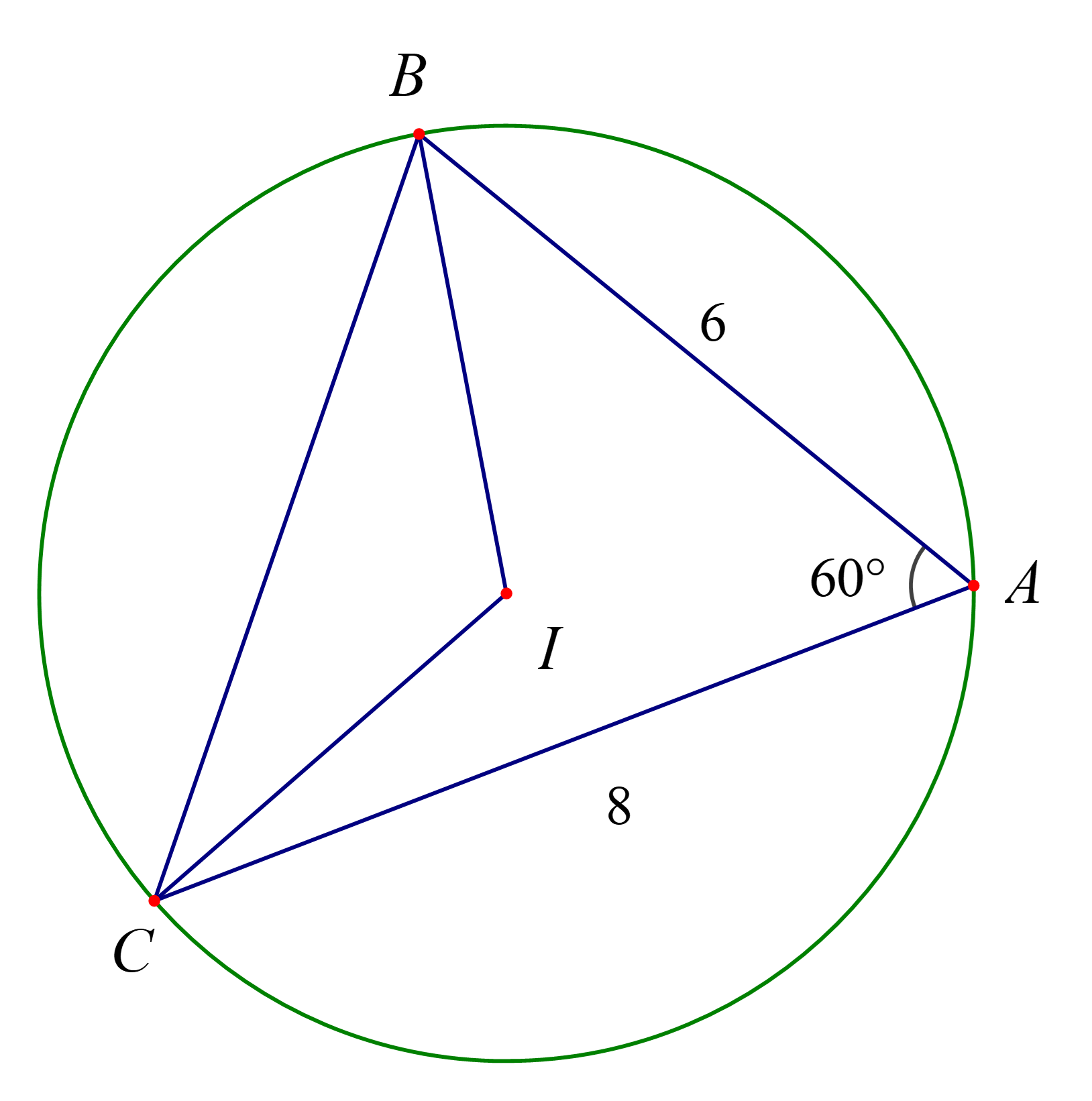
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.
Nửa chu vi của tam giác IBC:
Áp dụng công thức Heron ta tính được diện tích tam giác IBC:
Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).
Bài tập liên quan:
Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh .
b) Nêu kết quả trong trường hợp AC ⊥ BD.
Cách giải:
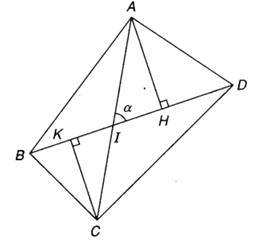
a) Ta có SABCD = SABD + SCBD.
Vẽ AH và CK vuông góc với BD tại H và K.
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có : AH = AI.sinα ; CK = CI.sinα.
⇒
b) Nếu AC ⊥ BD thì sinα = sin90° = 1, khi đó
Như vậy nếu tứ giác lồi có hai đường chéo vuông góc với nhau thì diện tích của tứ giác đó bằng một nửa tích độ dài của hai đường chéo.
Tham khảo thêm một số tài liệu liên quan:
20 câu Trắc nghiệm Giá trị lượng giác của một góc từ 0 độ đến 180 độ (Cánh diều) - Toán lớp 10
Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:
a) Các cạnh b = 14, c = 35 và .
b) Các cạnh a = 4, b = 5, c = 3.
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.
a) Chứng minh .
b) Biết rằng SABC = 9SBDE và DE = . Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.
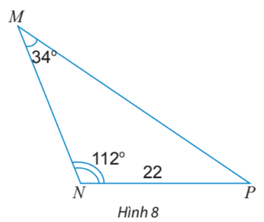
Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
Cho ha là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức ha = 2RsinBsinC.
Tính diện tích một cánh buồm hình tam giác. Biết cánh buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cạnh đó có số đo là 48° và 105° (Hình 12).

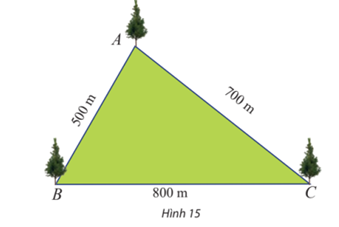
Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.
Cho tam giác ABC, biết cạnh a = 152, . Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.
Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh .
b) Nêu kết quả trong trường hợp AC ⊥ BD.
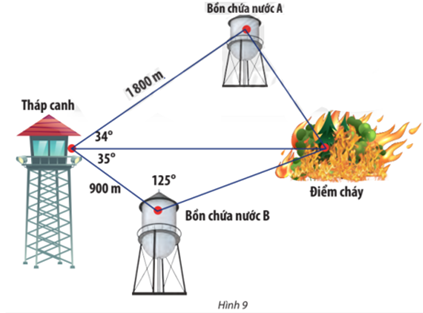
Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn ?
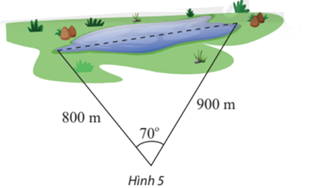
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70° (Hình 5).
Cho tam giác ABC có BC = a, AC = b, AB = c và (I; r) là đường tròn nội tiếp tam giác (Hình 11).
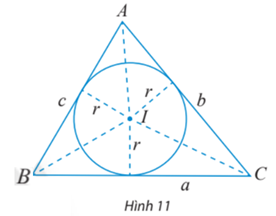
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: