Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
 Giải bởi Vietjack
Giải bởi Vietjack
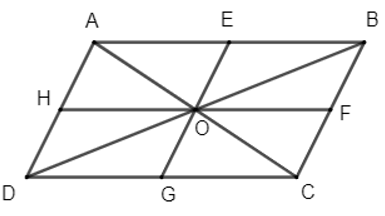
a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và OE = BC (1).
Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và OG = BC (2).
Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.
Chứng minh tương tự ta được O là trung điểm của HF.
Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.
b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.
Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Xác định một phép dời hình biến:
a) Tam giác AMQ thành tam giác CPN;
b) Tam giác AMO thành tam giác PCN.
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm N, P, C, A, M qua phép tịnh tiến theo vectơ
Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành.
a) Xác định điểm C đối xứng với B qua trục hoành.
b) Chứng minh rằng MB = MC.
c) Xác định điểm M sao cho tổng MA + MB đạt giá trị nhỏ nhất.
Xét phép đối xứng trục d (Hình 11).
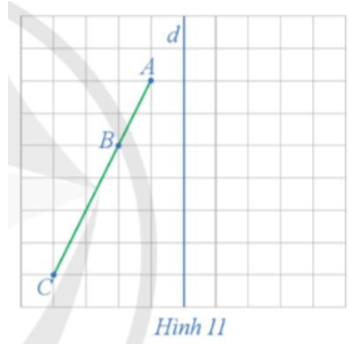
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
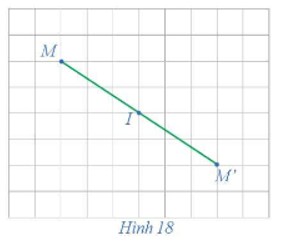
Trong mặt phẳng cho điểm I. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I) (Hình 18).
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Hình 41 là hình viên gạch men.
a) Xác định tâm đối xứng của viên gạch.
b) Xác định các trục đối xứng của viên gạch.
c) Xác định ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay φ = 90°.

Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE.
a) Xác định ảnh của các điểm D và C quay phép quay tâm A với góc quay φ = 60°.
b) Chứng minh rằng DC = BE.
c) Chứng minh rằng số đo góc giữa hai đường thẳng DC và BE bằng 60°.
Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F lần lượt biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.
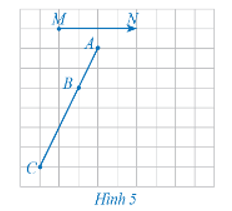
Xét phép tịnh tiến theo vectơ (Hình 5).
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép tịnh tiến trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Trong mặt phẳng cho đường thẳng d và điểm M. Dựng hình chiếu vuông góc M' của điểm M lên đường thẳng d (Hình 2).
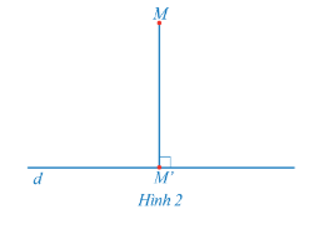
a) Có bao nhiêu hình chiếu vuông góc của điểm M trên đường thẳng d?
b) Có điểm nào của mặt phẳng không có hình chiếu vuông góc trên đường thẳng d hay không?
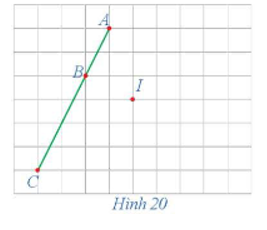
Xét phép đối xứng tâm I (Hình 20).
a) Xác định các điểm A', B', C' là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.