Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.
Giải bởi Vietjack
Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).
Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.
Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.
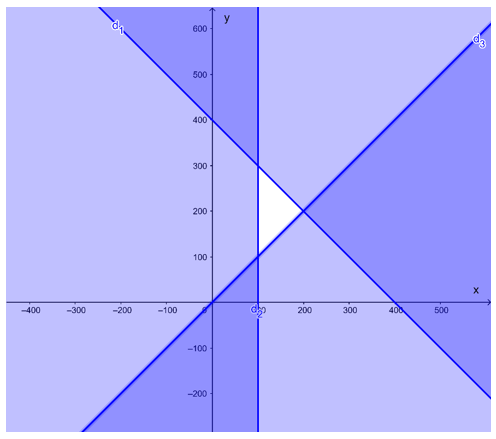
Từ đó ta có hệ bất phương trình sau: .
Ta vẽ bốn đường thẳng:
d1: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);
d2: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);
d3: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).
Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với như hình vẽ sau:
Một phân xưởng may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may 1 áo vest hết 2m vải và cần 20 giờ; 1 quần âu hết 1,5 m vải và cần 5 giờ. Xí nghiệp được giao sử dụng không quá 900 m vải và số giờ công không vượt quá 6 000 giờ. Theo khảo sát thị trường, số lượng quần bán ra không nhỏ hơn số lượng áo và không vượt quá 2 lần số lượng áo. Khi xuất ra thị trường, 1 chiếc áo lãi 350 nghìn đồng, 1 chiếc quần lãi 100 nghìn đồng. Phân xưởng cần may bao nhiêu áo vest và quần âu để thu được tiền lãi cao nhất (biết thị trường tiêu thụ luôn đón nhận sản phẩm của xí nghiệp).
Giá trị nhỏ nhất của biểu thức F = – x + y trên miền nghiệm của hệ bất phương trình .
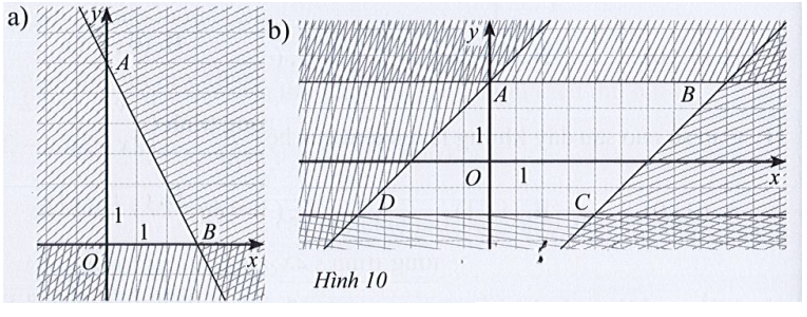
Viết hệ bất phương trình bậc nhất hai ẩn có miền nghiệm là miền đa giác không bị gạch ở mỗi Hình 10a, 10b.
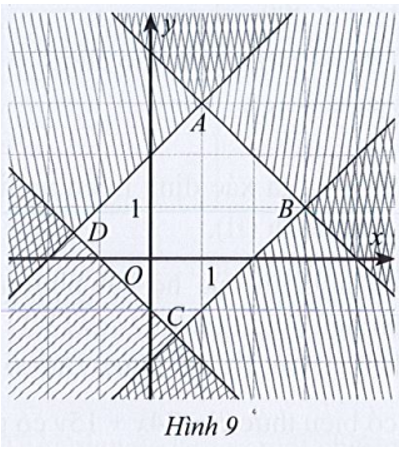
Miền đa giác ABCD ở Hình 9 là miền nghiệm của hệ bất phương trình:
Miền nghiệm của hệ bất phương trình là phần mặt phẳng chứa điểm có tọa độ:
b) Tìm x, y là nghiệm của hệ bất phương trình (III) sao cho F = 3x + 7y đạt giá trị lớn nhất, giá trị nhỏ nhất.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
