Bài I.7 trang 16 SBT Vật Lí 12: Một vật dao động điều hòa với tốc độ cực đại là $31,4cm/s$ . Lấy $\pi =3,14$. Tốc độ trung bình của vật trong một chu kì dao động là

A. $0$                                        B. $15cm/s$

C. $20cm/s$                             D. $10cm/s$

Phương pháp giải:

Sử dụng biểu thức tính tốc độ trung bình: $v_{tb}={\displaystyle \frac{s}{t}}$

Lời giải:

Quãng đường vật đi được trong một chu kì là: $s=4A$

Tốc độ trung bình của vật trong một chu kì: $v_{tb}={\displaystyle \frac{s}{t}}={\displaystyle \frac{4A}{T}}={\displaystyle \frac{4A}{{\displaystyle \frac{2\pi }{\omega }}}}={\displaystyle \frac{2}{\pi }}A\omega$

$={\displaystyle \frac{2}{\pi }}{v}_{max}={\displaystyle \frac{2}{\pi }}.31,4=20(cm/s)$

Chọn C

Bài I.8 trang 16 SBT Vật Lí 12: Một con lắc lò xo có độ cứng $36N/m$và khối lượng $m$. Biết thế năng của con lắc biến thiên tuần hoàn theo thời gian với tần số $6Hz$. Lấy ${\pi }^2=10$, khối lượng của vật là:

A. $50g$                                     B. $75g$

C. $100g$                                   D. $200g$

Phương pháp giải:

Sử dụng biểu thức liên hệ giữa tần số biến thiên tuần hoàn theo thời gian $f^{\prime }$ của thế năng và tần số biến thiên điều hòa theo thời gian $f$ của li độ: $f^{\prime }=2f$

Sử dụng công thức tính tần số dao động của con lắc lò xo: $f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}$

Lời giải:

Ta có: Mối liên giữa tần số biến thiên tuần hoàn theo thời gian $f^{\prime }$ của thế năng và tần số biến thiên điều hòa theo thời gian $f$ của li độ: $f^{\prime }=2f\Rightarrow f=3(Hz)$

Tần số dao động của con lắc lò xo:

$f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}$

$\Rightarrow m={\displaystyle \frac{k}{4{\pi }^2{f}^2}}$

$={\displaystyle \frac{36}{{\mathrm{4.10.3}}^2}}=0,1(kg)=100(g)$

Chọn C

Bài I.9 trang 16 SBT Vật Lí 12: Một con lắc lò xo dao động điều hòa theo trục $Ox$ nằm ngang. Con lắc gồm một vật có khối lượng $100g$ và một lò xo có độ cứng $100N/m$. Kéo vật tới vị trí có li độ bằng $2cm$ rồi truyền cho vật vận tốc $1,095m/s$ theo chiều dương. Chu kì và biên độ dao động của con lắc là

A. $0,2\mathrm{s};4cm$

B. $0,2\mathrm{s};2cm$

C. $2\pi (s);4cm$

D.$2\pi (s);10,9cm$

Phương pháp giải:

Sử dụng công thức tính chu kì con lắc lò xo: $T=2\pi \sqrt{{\displaystyle \frac{m}{k}}}$

Sử dụng công thức độc lập với thời gian giữa li độ và vận tốc: $A=\sqrt{x^2+{\displaystyle \frac{v^2}{{\omega }^2}}}$

Lời giải:

Tần số góc: $\omega =\sqrt{{\displaystyle \frac{k}{m}}}=\sqrt{{\displaystyle \frac{100}{0,1}}}=10\sqrt{10}(rad/s)$

Chu kì con lắc lò xo: $T={\displaystyle \frac{2\pi }{\omega }}={\displaystyle \frac{2\pi }{10\sqrt{10}}}=0,2(s)$

Đổi $v=1,095m/s=109,5cm/s$

Ta có: $A=\sqrt{x^2+{\displaystyle \frac{v^2}{{\omega }^2}}}$

$=\sqrt{2^2+{\displaystyle \frac{109,5^2}{{(10\sqrt{10})}^2}}}=4(cm)$

Chọn A

Bài I.10 trang 16 SBT Vật Lí 12: Một con lắc lò xo dao động theo trục $x$nằm ngang. Lò xo có độ cứng $100N/m$; vật có khối lượng $1,00kg$. Bỏ qua ma sát. Tại $t=0$ vật được kéo ra khỏi vị trí cân bằng cho lò xo dãn ra $10cm$ rồi thả không vận tốc đầu. Chọn gốc tọa độ tại vị trí cân bằng.

$a)$ Tính chu kì và biên độ dao động.

$b)$  Viết phương trình dao động.

$c)$  Tính cơ năng của con lắc.

Phương pháp giải:

a) Sử dụng công thức tính chu kì con lắc lò xo: $T=2\pi \sqrt{{\displaystyle \frac{m}{k}}}$

Sử dụng công thức độc lập với thời gian giữa li độ và vận tốc: $A=\sqrt{x^2+{\displaystyle \frac{v^2}{{\omega }^2}}}$

b) Vận dụng các bước viết phương trình dao động điều hòa: tìm $\omega$, tìm $A$, tìm pha ban đầu $\phi$

c) Sử dụng công thức tính cơ năng: $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2$

Lời giải:

a) Tần số góc: $\omega =\sqrt{{\displaystyle \frac{k}{m}}}=\sqrt{{\displaystyle \frac{100}{1}}}=10(rad/s)$

Chu kì con lắc lò xo: $T={\displaystyle \frac{2\pi }{\omega }}={\displaystyle \frac{2\pi }{10}}={\displaystyle \frac{\pi }{5}}(s)$

Tại $t=0:\{\begin{array}{l}x=10cm\\ v=0\end{array}$ :

Ta có: $A=\sqrt{x^2+{\displaystyle \frac{v^2}{{\omega }^2}}}=\sqrt{{10}^2+0}=10(cm)$

b) Tại $t=0:\{\begin{array}{l}x=A\cos \phi =A\\ v=-\sin \phi =0\end{array}\Rightarrow \phi =0$

phương trình dao động điều hòa là: $x=10\cos (10t)(cm)$

c) Cơ năng con lắc: $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2={\displaystyle \frac{1}{2}}.100.0,1^2=0,5(N)$

Bài I.11 trang 17 SBT Vật Lí 12: Hai con lắc đơn có chiều dài lần lượt là l1 và l2 và có chu kì lần lượt là T1, T2 tại một nơi có gia tốc rơi tự do là 9,8m/s2. Cho biết cũng tại nơi đó, con lắc đơn có chiều dài l1 + l2 có chu kì dao động là 2,4s và con lắc đơn có chiều dài l1 - l2 có chu kì dao động là 0,8s. Hãy tính T1, T2, l1 và l2. 

Sử dụng công thức tính chu kì dao động của con lắc đơn:  $T=2\pi \sqrt{{\displaystyle \frac{l}{g}}}$

Lời giải:

Ta có chu kì dao động của con lắc đơn: $T=2\pi \sqrt{{\displaystyle \frac{l}{g}}}$

 $\Rightarrow T^2\sim l$

+ Con lắc đơn có chiều dài $l=l_1+l_2$ sẽ dao động với chu kì $T=\sqrt{T_1^2+T_2^2}$

+ Con lắc đơn có chiều dài $l=l_1-l_2$ sẽ dao động với chu kì $T=\sqrt{T_1^2-T_2^2}$

Ta có hệ:

$\{\begin{array}{l}{T}_1^2+T_2^2=2,4^2\\ T_1^2-T_2^2=0,8^2\end{array}\iff \{\begin{array}{l}{T}_1=1,8\\ T_2=1,6\end{array}(s)$

+ $T_1=2\pi \sqrt{{\displaystyle \frac{l_1}{g}}}$$\iff 1,8=2\pi \sqrt{{\displaystyle \frac{l_1}{9,8}}}\Rightarrow l_1=0,8m$

+ $T_2=2\pi \sqrt{{\displaystyle \frac{l_2}{g}}}$$\iff 1,6=2\pi \sqrt{{\displaystyle \frac{l_2}{9,8}}}\Rightarrow l_2=0,64m$

Bài I.12 trang 17 SBT Vật Lí 12: Cho hai dao động điều hòa cùng phương, cùng tần số góc là $2\pi \left(ra\mathrm{d}/s\right)$ , có biên độ lần lượt $2cm$ và $4cm$, có pha ban đầu lần lượt là ${\displaystyle \frac{\pi }{6}}$ và ${\displaystyle \frac{\pi }{2}}(ra\mathrm{d})$.

a) Viết phương trình của hai dao động.

b) Biểu diễn trên cùng một giản đồ Fre-nen hai vectơ quay biểu diễn hai dao động trên.

c) Tìm phương trình dao động tổng hợp của hai dao động trên.

Phương pháp giải:

a) Sử dụng lí thuyết về phương trình dao động điều hòa

b) Vận dụng lí thuyết về giản đồ Fre-nen

c) Vận dụng công thức tổng hợp dao động điều hòa

Lời giải:

a) Phương trình dao động điều hòa của hai dao động là:

$\begin{array}{l}{x}_1=2\cos (2\pi t+{\displaystyle \frac{\pi }{6}})(cm)\\ x_2=4\cos (2\pi t+{\displaystyle \frac{\pi }{2}})(cm)\end{array}$

b) Hai vecto quay trên giản đồ Fre-nen

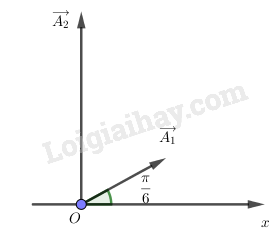
c)

$\begin{array}{l}{A}^2=A_1^2+A_2^2+2A_1{A}_2\cos \mathrm{\Delta }\phi \\ =2^2+4^2+\mathrm{2.2.4.}\cos ({\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{\pi }{6}})=28\\ \Rightarrow A=2\sqrt{7}cm\end{array}$

Ta có giản đồ Fre-nen:

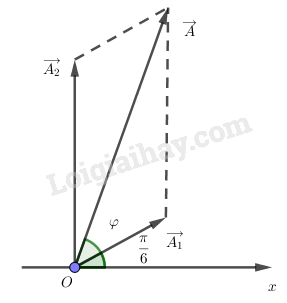
Ta có:

$\begin{array}{l}\tan \phi ={\displaystyle \frac{A_1\sin {\phi }_1+A_2\sin {\phi }_2}{A_1\cos {\phi }_1+A_2\cos {\phi }_2}}\\ ={\displaystyle \frac{2\sin {\displaystyle \frac{\pi }{6}}+4\sin {\displaystyle \frac{\pi }{2}}}{2\cos {\displaystyle \frac{\pi }{6}}+4\cos {\displaystyle \frac{\pi }{2}}}}={\displaystyle \frac{5\sqrt{3}}{3}}\\ \Rightarrow \phi =1,2(rad)\end{array}$

Phương trình dao động tổng hợp là: $x=2\sqrt{7}\cos (2\pi t+1,2)(cm)$

Bài I.13 trang 17 SBT Vật Lí 12: Một con lắc đơn có chiều dài dây treo $50cm$ và vật nhỏ có khối lượng $0,01kg$ mang điện tích $q=+{5.10}^{-6}C$, được coi là điện tích điểm. Con lắc dao động trong điện trường đều mà vectơ cường độ điện trường có độ lớn $E={10}^{4}V/m$ và hướng thẳng đứng xuống dưới. Lấy $g=10m/s^2$. Hỏi chu kì dao động điều hòa của con lắc là bao nhiêu?

Chú ý là lực gây ra gia tốc cho vật nặng là tổng hợp của trọng lực và lực điện tác dụng lên vật.

Phương pháp giải:

Sử dụng công thức tính chu kì dao động con lắc đơn $T=2\pi \sqrt{{\displaystyle \frac{l}{g}}}$

Sử dụng lí thuyết về con lắc đơn chịu tác dụng ngoại lực

Lời giải:

Khi chưa có ngoại lực tác dụng, chu kì con lắc đơn: $T=2\pi \sqrt{{\displaystyle \frac{l}{g}}}$

Khi có lực điện:

Ta có  $\overrightarrow{F_d}=q.\overrightarrow{E}$

Vì $q>0$ nên $\overrightarrow{F_d}$ có chiều hướng xuống dưới

$\begin{array}{l}\Rightarrow \overrightarrow{F_d}\uparrow \uparrow \overrightarrow{P}\\ \Rightarrow P^{\prime }=F_d+P=|q|E+mg=m{g}^{\prime }\\ \Rightarrow g^{\prime }=\frac{|q|E}{m}+g\end{array}$

Chu kì dao động con lắc khi chịu tác dụng ngoại lực:

$T^{\prime }=2\pi \sqrt{{\displaystyle \frac{l}{g^{\prime }}}}$$=2\pi \sqrt{{\displaystyle \frac{l}{{\displaystyle \frac{|q|E}{m}}+g}}}$$=2\pi \sqrt{{\displaystyle \frac{0,5}{{\displaystyle \frac{|{5.10}^{-6}|{.10}^4}{0,01}}+10}}}=1,15s$

Lời giải:

Tại vị trí li độ góc $\alpha$:

$\begin{array}{l}\{\begin{array}{l}{\mathrm{W}}_d={\displaystyle \frac{1}{2}}m{v}^2\\ {\mathrm{W}}_d=mgl(\cos \alpha -\cos {\alpha }_0)\end{array}\\ \Rightarrow v=\sqrt{2gl(\cos \alpha -\cos {\alpha }_0)}\end{array}$

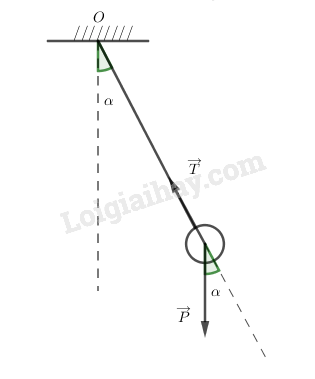
Áp dụng định luật II Niuton:

$\overrightarrow{T}+\overrightarrow{P}=m\overrightarrow{a}$

Chiếu theo phương hướng tâm:

$\begin{array}{l}T-P\cos \alpha =m{a}_{ht}=m{\displaystyle \frac{v^2}{l}}\\ \iff T=P\cos \alpha +m{\displaystyle \frac{v^2}{l}}\\ =mg\cos \alpha +2mg(\cos \alpha -\cos {\alpha }_0)\\ =mg(3\cos \alpha -2\cos {\alpha }_0)\end{array}$

$\begin{array}{l}\Rightarrow \{\begin{array}{l}{T}_{max}=mg(3-2\cos {\alpha }_0)(VTCB)\\ T_{min}=mg\cos {\alpha }_0(VTB)\end{array}\\ \Rightarrow {\displaystyle \frac{T_{max}}{T_{min}}}={\displaystyle \frac{3-2\cos {\alpha }_0}{\cos {\alpha }_0}}=1,02\\ \Rightarrow \cos {\alpha }_0=0,99\Rightarrow {\alpha }_0=0,115(rad)\end{array}$

Lời giải:

+ Chu kì dao động là $T={\displaystyle \frac{31,4}{100}}=0.314(s)$

Tần số góc:$\omega ={\displaystyle \frac{2\pi }{T}}={\displaystyle \frac{2\pi }{0,314}}=20(rad/s)$

+ Biên độ:

Tại $t=0:\{\begin{array}{l}x=2cm\\ v=-40\sqrt{3}cm/s\end{array}$

Ta có: $A=\sqrt{x^2+{\displaystyle \frac{v^2}{{\omega }^2}}}=\sqrt{2^2+{\displaystyle \frac{{(-40\sqrt{3})}^2}{{20}^2}}}=4(cm)$

+ Pha dao động ban đầu $\phi$

$$\begin{gathered} t=0:\{\begin{array}{l}x=A\cos \phi =2cm={\displaystyle \frac{A}{2}}\\ v=-A\omega \sin \phi =-40\sqrt{3}cm/s\end{array} \\ \Rightarrow \{\begin{array}{l}\cos \phi ={\displaystyle \frac{1}{2}}\\ \sin \phi >0\end{array}\Rightarrow \phi ={\displaystyle \frac{\pi }{3}}rad \end{gathered}$$

Vậy phương trình dao động: $x=4\cos (20t+{\displaystyle \frac{\pi }{3}})(cm)$