Với tóm tắt lý thuyết Tin học lớp 7 Bài 5: Thực hành mô phỏng các thuật toán tìm kiếm, sắp xếp sách Cánh diều hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Tin học7.
Tin học lớp 7 Bài 5: Thực hành mô phỏng các thuật toán tìm kiếm, sắp xếp
A. Lý thuyết Tin học 7 Bài 5: Thực hành mô phỏng các thuật toán tìm kiếm, sắp xếp
Bài 1. Cho dãy số ban đầu như sau:
![]()
Hãy mô phỏng thuật toán tìm kiếm tuần tự một số trong dãy số bằng cách trình bày diễn biến các bước thực hiện dưới dạng bảng.
a. Tìm x = 5.
b. Tìm x = 6.
Hướng dẫn
a. Tìm x = 5.
|
Bước |
Thực hiện |
|
1 |
So sánh số ở đầu dãy với x: Vì a1 = 8 ≠ x nên chuyển sang xét số tiếp theo a2 trong dãy. |
|
2 |
So sánh số đang xét với x: Vì a2 = 17 ≠ x nên chuyển sang xét số tiếp theo a3 trong dãy. |
|
3 |
So sánh số đang xét với x: Vì a3 = 23 ≠ x nên chuyển sang xét số tiếp theo a4 trong dãy. |
|
4 |
So sánh số đang xét với x: Vì a4 = 1 ≠ x nên chuyển sang xét số tiếp theo a5 trong dãy. |
|
5 |
So sánh số đang xét với x: Vì a5 = 12 ≠ x nên chuyển sang xét số tiếp theo a6 trong dãy. |
|
6 |
So sánh số đang xét với x: Vì a6 = 7 ≠ x nên chuyển sang xét số tiếp theo a7 trong dãy. |
|
7 |
So sánh số đang xét với x: Vì a7 = 5 = x. Kết luận: Tìm thấy x ở vị trí thứ bảy trong dãy; kết thúc thuật toán. |
b. Tìm x = 6.
|
Bước |
Thực hiện |
|
1 |
So sánh số ở đầu dãy với x: Vì a1 = 8 ≠ x nên chuyển sang xét số tiếp theo a2 trong dãy. |
|
2 |
So sánh số đang xét với x: Vì a2 = 17 ≠ x nên chuyển sang xét số tiếp theo a3 trong dãy. |
|
3 |
So sánh số đang xét với x: Vì a3 = 23 ≠ x nên chuyển sang xét số tiếp theo a4 trong dãy. |
|
4 |
So sánh số đang xét với x: Vì a4 = 1 ≠ x nên chuyển sang xét số tiếp theo a5 trong dãy. |
|
5 |
So sánh số đang xét với x: Vì a5 = 12 ≠ x nên chuyển sang xét số tiếp theo a6 trong dãy. |
|
6 |
So sánh số đang xét với x: Vì a6 = 7 ≠ x nên chuyển sang xét số tiếp theo a7 trong dãy. |
|
7 |
So sánh số đang xét với x: Vì a7 = 5 ≠ x nên chuyển sang xét số tiếp theo a8 trong dãy. |
|
8 |
So sánh số đang xét với x: Vì a8 = 1 ≠ x nên chuyển sang xét số tiếp theo a9 trong dãy. |
|
9 |
So sánh số đang xét với x: Vì a9 = 13 ≠ x nên chuyển sang xét số tiếp theo a10 trong dãy. |
|
10 |
So sánh số đang xét với x: Vì a10 = 10 ≠ x nên kết thúc dãy số. Kết luận: Không tìm thấy x = 6 trong dãy; kết thúc thuật toán. |

Gợi ý: Dựa theo các làm bài trong Bài “Sắp xếp chọn”.
Hướng dẫn
|
Dãy |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
Giải thích |
|
Ban đầu |
8 |
17 |
23 |
1 |
12 |
7 |
5 |
1 |
13 |
10 |
Tiếp theo: đổi chỗ 23 và a1 |
|
Sau B1 |
23 |
17 |
8 |
1 |
12 |
7 |
5 |
1 |
13 |
10 |
Tiếp theo: Không đổi chỗ |
|
Sau B2 |
23 |
17 |
8 |
1 |
12 |
7 |
5 |
1 |
13 |
10 |
Tiếp theo: đổi chỗ 13 và a3 |
|
Sau B3 |
23 |
17 |
13 |
1 |
12 |
7 |
5 |
1 |
8 |
10 |
Tiếp theo: đổi chỗ 12 và a4 |
|
Sau B4 |
23 |
17 |
13 |
12 |
1 |
7 |
5 |
1 |
8 |
10 |
Tiếp theo: đổi chỗ 10 và a5 |
|
Sau B5 |
23 |
17 |
13 |
12 |
10 |
7 |
5 |
1 |
8 |
1 |
Tiếp theo: đổi chỗ 8 và a6 |
|
Sau B6 |
23 |
17 |
13 |
12 |
10 |
8 |
5 |
1 |
7 |
1 |
Tiếp theo: đổi chỗ 7 và a7 |
|
Sau B7 |
23 |
17 |
13 |
12 |
10 |
8 |
7 |
1 |
5 |
1 |
Tiếp theo: đổi chỗ 5 và a8 |
|
Sau B8 |
23 |
17 |
13 |
12 |
10 |
8 |
7 |
5 |
1 |
1 |
Tiếp theo: không đổi chỗ |
|
Sau B9 |
23 |
17 |
13 |
12 |
10 |
8 |
7 |
5 |
1 |
1 |
Tiếp theo: không đổi chỗ |
|
Dãy kết quả |
23 |
17 |
13 |
12 |
10 |
8 |
7 |
5 |
1 |
1 |
|
Gợi ý: Dựa theo các làm bài trong Bài “Sắp xếp nổi bọt”.

Hướng dẫn
Diễn biến các bước của thuật toán sắp xếp nổi bọt để sắp xếp dãy số theo chiều không tăng là:
Lượt thứ nhất:
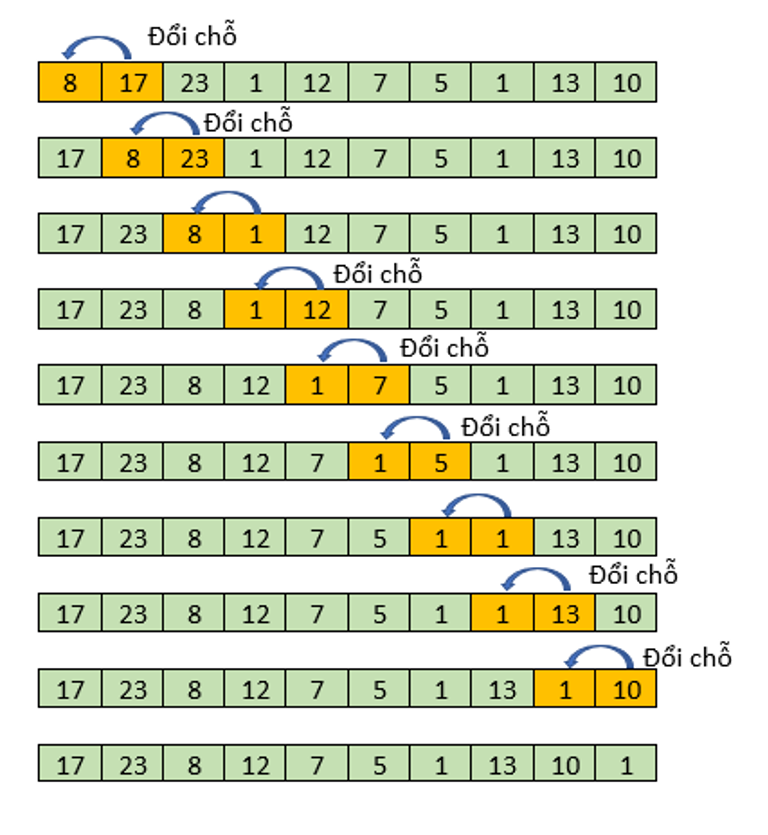
Sau đó thực hiện các lượt đổi cho cho đến khi sắp xếp dãy số theo chiều giảm dần.
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
|
23 |
17 |
13 |
12 |
10 |
8 |
7 |
5 |
1 |
1 |
a. Tìm x = 5.
b. Tìm x = 6.
Hướng dẫn
a. Tìm x = 5.
Chia đôi lần 1: Phạm vi tìm kiếm là dãy từ a1 đến a10. Lấy a5 là số có vị trí giữa dãy; Vì x < a5 nên nửa đầu dãy chắc chắn không chứa x = 5, tiếp theo tìm trong nửa sau của dãy. Như vậy, phạm vi tìm kiếm tiếp theo là dãy từ a6 đến a10.
Chia đôi lần 2: Phạm vi tìm kiếm là dãy từ a6 đến a10. Lấy a8 là số có vị trí giữa dãy. Vì x = a8 nên kết thúc thuật toán với kết quả: Tìm thấy x ở vị trí thứ tám.
b. Tìm x = 6.
Chia đôi lần 1: Phạm vi tìm kiếm là dãy từ a1 đến a10. Lấy a5 là số có vị trí giữa dãy; Vì x < a5 nên nửa đầu dãy chắc chắn không chứa x = 6, tiếp theo tìm trong nửa sau của dãy. Như vậy, phạm vi tìm kiếm tiếp theo là dãy từ a6 đến a10.
Chia đôi lần 2: Phạm vi tìm kiếm là dãy từ a6 đến a10. Lấy a8 là số có vị trí giữa dãy. Vì x > a8 nên nửa sau dãy chắc chắn không chứa x = 6, tiếp theo tìm trong nửa đầu của dãy này. Như vậy, phạm vi tìm kiếm tiếp theo là dãy từ a5 đến a7.
Chia đôi lần 3: Phạm vi tìm kiếm là dãy từ a5 đến a7. Lấy a6 là số có vị trí giữa dãy. Vì x < a6 nên nửa đầu dãy chắc chắn không chứa x = 6, tiếp theo tìm trong nửa sau của dãy này. Như vậy, phạm vi tìm kiếm tiếp theo là a7.
Phạm vi tìm kiếm chỉ còn một số nhưng không tìm thấy x. Kết thúc thuật toán với kết quả: Không có x trong dãy.
B. Bài tập trắc nghiệm Tin học 7 Bài 5: Thực hành mô phỏng các thuật toán tìm kiếm, sắp xếp
Đang cập nhật.
Xem thêm các bài tóm tắt lý thuyết Tin học 7 Cánh diều hay, chi tiết khác:
Lý thuyết Tin học 7 Bài 1: Tìm kiếm tuần tự
Lý thuyết Tin học 7 Bài 2: Tìm kiếm nhị phân
Lý thuyết Tin học 7 Bài 3: Sắp xếp chọn
Lý thuyết Tin học 7 Bài 4: Sắp xếp nổi bọt
Lý thuyết Tin học 7 Bài 5: Thực hành mô phỏng các thuật toán tìm kiếm, sắp xếp