Với Đề thi đánh giá năng lực Đại học Quốc gia Hà Nội năm 2022 sẽ giúp học sinh ôn luyện đề thi ĐGNL đạt kết quả tốt.
Để mua trọn bộ Đề ôn thi ĐGNL Đại học Quốc gia Hà Nội năm 2023 bản word có lời giải chi tiết, đẹp mắt, quý Thầy/Cô vui lòng truy cập tailieugiaovien.com.vn
Bộ Giáo dục và Đào tạo
Trường Đại học Quốc gia Hà Nội
Đề thi Đánh giá năng lực năm 2021 - 2022
Thời gian làm bài: 195 phút
|
Thời gian làm bài: |
195 phút (không kể thời gian phát đề). |
|
Tổng số câu hỏi: |
150 câu. |
|
Dạng câu hỏi: |
Trắc nghiệm 4 lựa chọn (Chỉ có 1 phương án đúng) và điền đáp án. |
|
Cách làm bài: |
Làm bài trên phiếu trả lời trắc nghiệm. |
CẤU TRÚC BÀI THI
|
Nội dung |
Số câu |
Thời gian (phút) |
|
|
Phần 1: Tư duy định lượng – Toán học |
50 |
75 |
|
|
Phần 2: Tư duy định tính – Ngữ văn |
50 |
60 |
|
|
Phần 3: Khoa học |
3.1. Lịch sử |
10 |
60 |
|
3.2. Địa lí |
10 |
||
|
3.3. Vật lí |
10 |
||
|
3.4. Hóa học |
10 |
||
|
3.5. Sinh học |
10 |
||
PHẦN 1. TƯ DUY ĐỊNH LƯỢNG – Lĩnh vực: Toán học
Câu 1 (NB): Dưới đây là điểm chuẩn lớp 10 các trường top đầu tại Hà Nội (2014-2018)
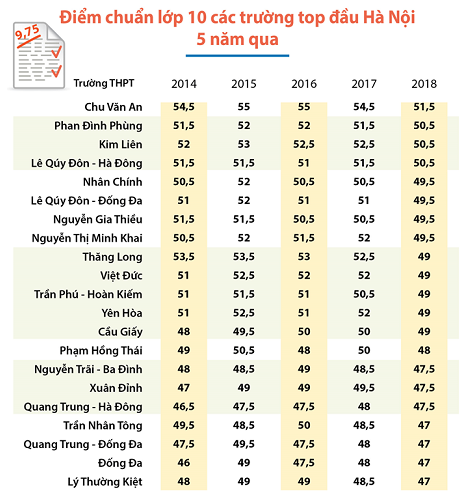
(Nguồn: Sở GD & ĐT Hà Nội)
Năm 2018 điểm đầu vào của trường THPT nào cao nhất?
A. Lê Quý Đôn - Hà Đông B. Phan Đình Phùng
C. Chu Văn An D. Phạm Hồng Thái
Câu 2 (NB): Một chất điểm chuyển động theo phương trình S = t3 + 5t2 - 5, trong đó t > 0, t được tính bằng giây (s) và S được tính bằng mét (m). Tính vận tốc của chất điểm tại thời điểm t = 2 (giây).
A. 32 m/s B. 22 m/s C. 27 m/s D. 28 m/s
Câu 3 (NB): Phương trình 32x + 1 = 27 có nghiệm là

Câu 4 (VD): Số nghiệm của hệ phương trình 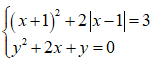 là:
là:
A. 1 B. 2 C. 3 D. 4
Câu 5 (VD): Cho các số phức z1, z2 thỏa mãn |z1| = 3, |z2| = 4 và |z1 - z2| = 5. Gọi A, B lần lượt là điểm biểu diễn các số phức z1, z2. Diện tích S của tam giác OAB với O là gốc tọa độ là:
A. . B. S = 5√2 C. S = 6 D. S = 12
Câu 6 (TH): Trong không gian Oxyz, mặt phẳng đi qua điểm M(1; 2 ; 3) và song song với mặt phẳng (P): x - 2y + z + 3 = 0 có phương trình là:
A. x - 2y + z + 3 = 0
B. x + 2y + 3z = 0
C. x - 2y + z = 0
D. x - 2y + z - 8 = 0
Câu 7 (NB): Trong không gian Oxyz, hình chiếu vuông góc của điểm M(1; 6; 2020) trên mặt phẳng (Oxy) có tọa độ là:
A. (1; 0; 2020) B. (0; 6; 2020) C. (1; 6; 0) D. (1; 0; 0)
Câu 8 (VD): Số nguyên x lớn nhất để đa thức  luôn âm là
luôn âm là
A. x = 2 B. x = 1 C. x = -2 D. x = -1
Câu 9 (TH): Phương trình sin 2x + cos x = 0 có tổng các nghiệm trong khoảng (0; 2π) bằng:
A. 6π B. 2π C. 3π D. 5π
Câu 10 (VD): Ông Nam đã trồng cây ca cao trên mảnh đất của mình có dạng hình tam giác, ông trồng ở hàng đầu tiên 3 cây ca cao, kể từ hàng thứ hai trở đi số cây phải trồng ở mỗi hàng nhiều hơn 5 cây so với số cây đã trồng ở hàng trước đó và ở hàng cuối cùng ông đã trồng 2018 cây ca cao. Số cây ca cao mà ông Nam đã trồng trên mảnh đất của mình là
A. 408.242 cây. B. 407.231 cây. C. 407.232 cây. D. 408.422 cây.
Câu 11 (TH): Biết F(x) là một nguyên hàm của hàm số 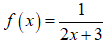 và F(0) = 0. Tính F(2) .
và F(0) = 0. Tính F(2) .

Câu 12 (VD): Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới :
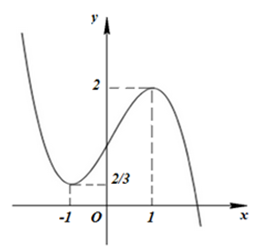
Số giá trị nguyên dương của m để phương trình f(x2 - 4x + 5) + 1 = m có nghiệm là
A. 0 B. Vô số C. 4 D. 3
Câu 13 (VD): Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t) = 7t (m/s). Đi được 5s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = -70 (m/s2). Tính quãng đường S đi được của ô tô lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. S = 95,7 (m) B. S = 96,25 (m) C. S = 94 (m) D. S = 87, 5 (m)
Câu 14 (TH): Một người gửi tiết kiệm 200 triệu đồng với lãi suất 5% một năm và lãi hàng năm được nhập vào vốn. Sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 3003 triệu đồng?
A. 11 (năm). B. 10 (năm). C. 8 (năm). D. 9 (năm).
Câu 15 (TH): Tập nghiệm của bất phương trình là:
A. (0; 4] B. (0; 2] C. [2; 4] D. [1; 4]
Câu 16 (TH): Diện tích hình phẳng giới hạn bởi các đường y = 7 - 2x3, y = x2 + 4 bằng:
A. 5 B. 3 C. 4 D.
Câu 17 (VD): Có bao nhiêu số nguyên m để hàm số f(x) = x4 - 2(m2 - 3m)x2 + 3 đồng biến trên khoảng (2;+∞)
A. 4 B. 6 C. 2 D. 5
Câu 18 (TH): Nghiệm của phương trình (3 + i)z + (4 - 5i) = 6 - 3i là

Câu 19 (VD): Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn |(1 + i)z - 5 + i| = 2 là một đường tròn tâm I và bán kính R lần lượt là:
A. I(2; -3), R = √2 B. I(2; -3), R = 2 C. I(-2; 3), R = √2 D. I(-2; 3), R = 2
Câu 20 (VD): Diện tích hình vuông có bốn đỉnh nằm trên hai đường thẳng song song d1: 2x - 4y + 1 = 0 và d2: -x + 2y + 10 = 0 là:

Câu 21 (VD): Cho x2+ y2 - 2xcosα - 2ysinα - cos2α = 0 Xác định α để (C) có bán kính lớn nhất:
A. B. C. D.
Câu 22 (VD): Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1;2;-1); B(2;1;0) và mặt phẳng (P): 2x + y + 3z + 1 = 0. Gọi (Q) là mặt phẳng chứa A; B và vuông góc với (P). Phương trình mặt phẳng (Q) là:
A. 2x + 5y + 3z - 9 = 0 B. 2x + y - 3z - 9 = 0 C. 2x + y - z - 5 = 0 D. x + 2y - z - 6 = 0
Câu 23 (TH): Biết rằng thiết diện qua trục của một hình nón là tam giác đều có diện tích bằng . Tính thể tích khối nón đã cho.

Câu 24 (VD): Một hình trụ (T) có hai đáy là hai hình tròn (O;r) và (O';r). Khoảng cách giữa hai đáy là OO' = . Một hình nón (N) có đỉnh là O' và đáy là hình tròn (O;r). Gọi S1, S2 lần lượt là diện tích xung quanh của (T) và (N). Khi đó tỉ số bằng
A. B. 1 C. 2 D.
Câu 25 (VD): Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình chữ nhật, 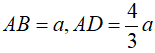 . Biết A' cách đều các đỉnh A, B, C và cạnh bên AA' = a Thể tích của khối lăng trụ đã cho bằng:
. Biết A' cách đều các đỉnh A, B, C và cạnh bên AA' = a Thể tích của khối lăng trụ đã cho bằng:

.......................................
.......................................
.......................................