Với Đề thi đánh giá năng lực Đại học Quốc gia Hà Nội năm 2021 sẽ giúp học sinh ôn luyện đề thi ĐGNL đạt kết quả tốt.
Để mua trọn bộ Đề ôn thi ĐGNL Đại học Quốc gia Hà Nội năm 2023 bản word có lời giải chi tiết, đẹp mắt, quý Thầy/Cô vui lòng truy cập tailieugiaovien.com.vn
Bộ Giáo dục và Đào tạo
Trường Đại học Quốc gia Hà Nội
Đề thi Đánh giá năng lực năm 2021 - 2022
Thời gian làm bài: 120 phút
Câu 1. Hình vẽ dưới đây mô tả số người nhiễm Covid 23/01/2020 đến ngày 13/02/2021.
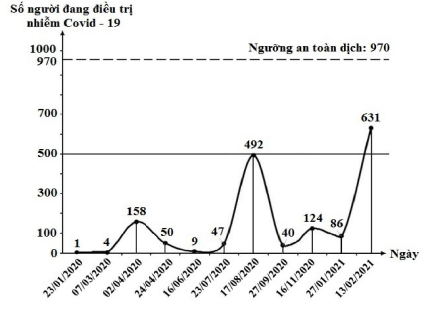
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, nhiều nhất?
A. 16/11/2020
B. 17/08/2020
C. 23/07/2020
D. 13/02/2021
Câu 2 Một vật rơi tự do theo phương thẳng đứng có quãng đường dịch chuyển 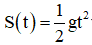 với t là thời gian tính bằng giây (s) kể từ lúc vật bắt đầu rơi. S la quãng đường tính bằng mét (m), g = 9,8 m/s2. Vận tốc tức thời của vật tại thời điểm t = 4s
với t là thời gian tính bằng giây (s) kể từ lúc vật bắt đầu rơi. S la quãng đường tính bằng mét (m), g = 9,8 m/s2. Vận tốc tức thời của vật tại thời điểm t = 4s
A. 156,8 m/s.
B. 78, 4 m/s.
C. 19,6 m/s.
D. 39, 2 m/s.
Câu 3. Phương trình log3(3x + 6) = 4 có nghiệm là:
A. x = 25.
B. x = 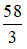
C. x = 2
D. x = 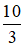
Câu 4. Hệ phương trình sau có bao nhiêu nghiệm ?
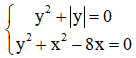
A. 1 B. 3 C. 2 D. 4
Câu 5. Trên mặt phẳng toạ độ Oxy, gọi M, N, P theo thứ tự là các điểm biểu diễn các số phức z1 = 3 - 2i, z2 = 5 - 10i, z3 = 10 + 3i. Toạ độ trọng tâm của tam giác MNP là
A. (5; -3)
B. (6; -3)
C. (-3; 6)
D. (6; 2)
Câu 6. Trong không gian Oxyz, mặt phẳng (P) đi qua điểm M(2; -3; 4) và vuông góc với trục Oy có phương trình là
A. y = 3.
B. x = 2.
C. z = 4.
D. y = -3.
Câu 7. Trong không gian Oxyz, cho điểm M(1; 2; 3). Tìm toạ độ điểm M’ đối xứng với M qua trục Oz.
A. M'(1; -2;3).
B. M'( -1; 2; -3).
C. M'(- 1; -2; 3).
D. M'( -1; -2; -3)
Câu 8. Bất phương trình có số nghiệm 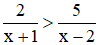 nguyên thuộc đoạn [0, 10] là
nguyên thuộc đoạn [0, 10] là
A. 2 B. 3 C. 8 D. 9
Câu 9. Số nghiệm của phương trình sin x + 3 cos x = 2sin 2x thuộc khoảng (0, 2π) là
A. 1 B. 4 C. 8 D. 5
Câu 10. Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng tháng thứ 7 người đó nhận được lương là bao nhiêu?
A. 7,0 triệu
B. 7,3 triệu
C. 7,2 triệu
D. 7,4 triệu
Câu 11. Họ nguyên hàm của hàm số trên 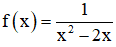 khoảng (2; +∞)
khoảng (2; +∞)
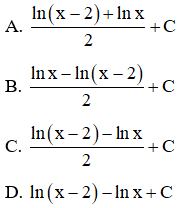
Câu 12. Cho hàm số f(x) có bảng biến thiên như hìn vẽ
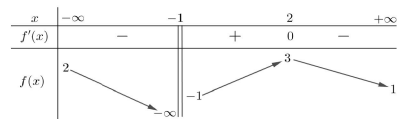
Tìm điều kiện của tham số m để m < f(x) + x2 với mọi x ∈ (1; 2)
A. m ≤ f (2) + 4
B. m < f (1) +1
C. m < f (2) + 4
D. m ≤ f (1) + 1
Câu 13. Một chất điểm chuyển động thẳng với vận tốc v(t) = 2t + 3 (m/s) , với t là thời gian tính bằng giây (s) từ lúc chất điểm bắt đầu chuyển động. Tính quãng đường chất điểm đi được trong khoảng thời gian từ giây thứ nhất đến giây thứ năm
A. 24 m
B. 36 m
C. 30 m
D. 40m
Câu 14. Một thiết bị trong năm 2021 được định giá 100 triệu đồng. Trong 5 năm tiếp theo, mỗi năm giá trị thiết bị giảm 6% so với năm trước và từ năm thứ 6 trở đi, mỗi năm giá trị thiết bị giảm 10% so với năm trước. Hỏi bắt đầu từ năm nào thì giá trị thiết bị nhỏ hơn 50 triệu đồng?
A. 2032
B. 2029
C. 2031
D. 2030
Câu 15. Tập nghiệm của bất phương trình 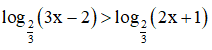
Câu 16. Cho (H) là hình phẳng giới hạn bởi các đường và y = x2. Thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox bằng
Câu 17. Tập hợp các giá trị của tham số m để hàm số y = 2x2 - mx + m đồng biến trên khoảng (1; +∞) là
A. (-∞; 4]
B. (-∞; 2]
C. [2; +∞)
D. [4; +∞)
Câu 18. Phương trình (3 + 2i)z - (4 + 9i) = 2 - 5i có nghiệm là
A. z = i.
B. z = 2i.
C. z = 1.
D. z = 2.
Câu 19. Xét các số phức z thoả mãn 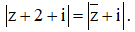 Tập hợp điểm biểu diễn các số phức z là đường thẳng có phương trình
Tập hợp điểm biểu diễn các số phức z là đường thẳng có phương trình
A. x - y + 1 = 0
B. x + y + 1 = 0
C. x + 1 = 0
D. 2x + 2y + 3 =0
Câu 20. Trên mặt phẳng toạ độ Oxy, cho tam giác ABC có toạ độ các đỉnh là A(2; 3), B(5; 0) và C(-1; 0). Tìm toạ độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC.
A. (0;0)
B. (1;0)
C. (2;0)
D. (3;0)
Câu 21. Trên mặt phẳng toạ độ Oxy, cho đường tròn (Cm): x2 + y2 - 6x - 2my + 6m - 16 = 0, với m là tham số thực. Khi m thay đổi, bán kinh đường tròn (Cm) đạt giá trị nhỏ nhất bằng bao nhiêu:
A. 5 B. 4 C. 3 D.
.......................................
.......................................
.......................................