Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết, bài tập về Điện xoay chiều hay nhất - Vật lí 12, tài liệu bao gồm 14 trang, đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi  tốt nghiệp THPT môn Vật Lý sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

CHƯƠNG 3: DÒNG ĐIỆN XOAY CHIỀU

I. KHÁI NIỆM DÒNG ĐIỆN XOAY CHIỀU

1) Định nghĩa

Dòng điện xoay chiều là dòng điện có cường độ biến thiên tuần hoàn theo thời gian (theo hàm cos hay sin của thời gian).

2) Biểu thức: i = I₀cos(ωt + φi) A

trong đó:

     i: giá trị cường độ dòng điện xoay chiều tức thời, đơn vị là (A)

     I₀ > 0: giá trị cường độ dòng điện cực đại của dòng điện xoay chiều

     ω, φ_i : là các hằng số.

     ω > 0 là tần số góc.

     (ωt + φ_i): pha tại thời điểm t.

     φi : Pha ban đầu của dòng điện.

3) Chu kỳ, tần số của dòng điện

     Chu kì, tần số của dòng điện: \(\left\{ \begin{array}{l}T = \frac{{2\pi }}{\omega } = \frac{1}{f}(s)\\f = \frac{1}{T} = \frac{\omega }{{2\pi }}(Hz)\end{array} \right.\)

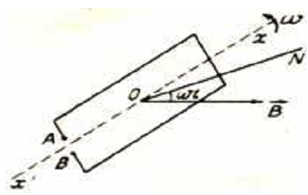
     Cho khung dây dẫn có diện tích S gồm có N vòng dây quay đều với vận tốc góc ω xung quanh trục đối xứng x’x trong từ trường đều có \(\vec B \bot \) xx '. Tại t = 0 giả sử \(\vec n \equiv \vec B\)

     Sau khoảng thời t, n quay được một góc ωt. Từ thông gởi qua khung là F = NBScos(ωt) Wb.

     Đặt Φo = NBS Þ Φ = Φocos(ωt), Φo được gọi là từ thông cực đại. Theo hiện tượng cảm ứng điện từ trong khung hình thành suất điện động cảm ứng có biểu thức e = – Φ’ = ωNBSsin(ωt).

     Đặt E₀ = ωNBS = ωΦ₀ Þ e = E₀sin(ωt) = E₀cos(ωt - )

     Vậy suất điện động trong khung dây biến thiên tuần hoàn với tần số góc ω và chậm pha hơn từ thông góc π/2. Nếu mạch ngoài kín thì trong mạch sẽ có dòng điện, điện áp gây ra ở mạch ngoài cũng biến thiên điều hòa: u = U₀cos(ωt + φu) V.

     Đơn vị : S (m²), Φ (Wb) – Webe, B (T) – Testla, N (vòng), ω (rad/s), e (V)…

 Chú ý: 1 vòng/phút = \[\] = \[\] ( rad/s ); 1 cm² = 10^{- 4} m²

III. ĐỘ LỆCH PHA CỦA ĐIỆN ÁP VÀ DÒNG ĐIỆN

     Đặt φ = φ_u – φ_i, được gọi là độ lệch pha của điện áp và dòng điện trong mạch.

     Nếu φ > 0 thi khi đó điện áp nhanh pha hơn dòng điện hay dòng điện chậm pha hơn điện áp.

     Nếu φ âm thì khi đó điện áp chậm pha hơn dòng điện hay dòng điện nhanh pha hơn điện áp.

Chú ý:

     - Khi độ lệch pha của điện áp và dòng điện là π/2 thì ta có phương trình của dòng điện và điện áp thỏa mãn \(\left\{ \begin{array}{l}u = {U_0}\cos (\omega t)\\i = {I_0}\cos (\omega t \pm \frac{\pi }{2}) =  \mp {I_0}\sin (\omega t)\end{array} \right.\) Þ \({\left( {\frac{u}{{{U_0}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\)

     - Nếu điện áp vuông pha với dòng điện, đồng thời tại hai thời điểm t₁, t₂ điện áp và dòng điện có các cặp giá trị tương ứng là u₁; i₁ và u₂; i₂ thì ta có: \({\left( {\frac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{{i_1}}}{{{I_0}}}} \right)^2}\)= \({\left( {\frac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{{i_2}}}{{{I_0}}}} \right)^2}\) à \(\frac{{{U_0}}}{{{I_0}}} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_1^2 - i_2^2}}} \)

IV. CÁC GIÁ TRỊ HIỆU DỤNG

     Cho dòng điện xoay chiều i = I₀cos(ωt + φ) A chạy qua R, công suất tức thời tiêu thụ trên R:

     p = Ri² = RI\(_0^2\)cos²(wt +j) = RI\(_0^2\)\(\frac{{1 + \cos (2\omega t + 2\phi )}}{2}\)= \(\frac{{RI_0^2}}{2} + \frac{{RI_0^2}}{2}\cos (2\omega t + 2\phi )\)

     Giá trị trung bình của p trong 1 chu kì: \(\bar p = \)\(\frac{{RI_0^2}}{2} + \frac{{RI_0^2}}{2}\overline {\cos (2\omega t + 2\phi )} \) = \(\frac{{RI_0^2}}{2}\)

     Kết quả tính toán, giá trị trung bình của công suất trong 1 chu kì (công suất trung bình): P = \(\bar p\) = \(\frac{{RI_0^2}}{2}\)

     Nhiệt lượng tỏa ra khi đó là Q = P.t = \(\frac{{I_0^2}}{2}Rt\)

     Cũng trong cùng khoảng thời gian t cho dòng điện không đổi (dòng điện một chiều) qua điện trở R nói trên thì nhiệt lượng tỏa ra là Q’ = I²Rt.

     Cho Q = Q’ Û \(\frac{{I_0^2}}{2}Rt\) = I²Rt Þ I = \(\frac{{{I_0}}}{{\sqrt 2 }}\)

     I được gọi là giá trị hiệu dụng của cường độ dòng điện xoay chiều hay cường độ hiệu dụng.

     Tương tự, ta cũng có điện áp hiệu dụng và suất điện động hiệu dụng là U = \(\frac{{{U_0}}}{{\sqrt 2 }}\); E = \(\frac{{{E_0}}}{{\sqrt 2 }}\)

     Ngoài ra, đối với dòng điện xoay chiều, các đại lượng như điện áp, suất điện động, cường độ dòng điện , … cũng là hàm số sin hay cosin của thời gian, với các đại lượng này.

Chú ý :

Trong mạch điện xoay chiều các đại lượng có sử dụng giá trị tức thời là: \(\left\langle \begin{array}{l}u = {U_0}\cos (\omega t + {\phi _u})\\i = {I_0}\cos (\omega t + {\phi _i})\\e = {E_0}\cos (\omega t + {\phi _e})\\p = {i^2}R = I_0^2R{\cos ^2}(\omega t + {\phi _i})\end{array} \right.\)

và các đại lượng sử dụng giá trị hiệu dụng là cường độ dòng điện I, điện áp U, suất điện động E.

BÀI GIẢNG MẠCH ĐIỆN XOAY CHIỀU CÓ 2 PHẦN TỬ

I. MẠCH ĐIỆN XOAY CHIỀU GỒM R, L

Đặc điểm:

Điện áp và tổng trở của mạch: \(\left\{ \begin{array}{l}{U_{RL}} = \sqrt {U_R^2 + U_L^2} \\{Z_{RL}} = \sqrt {{R^2} + Z_L^2} \end{array} \right.\)

Định luật Ohm cho đoạn mạch: \(\left\{ \begin{array}{l}I = \frac{{{U_{RL}}}}{{{Z_{RL}}}} = \frac{{\sqrt {U_R^2 + U_L^2} }}{{\sqrt {R_{}^2 + Z_L^2} }} = \frac{{{U_R}}}{U} = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{I_0}}}{{\sqrt 2 }}\\{I_0} = \frac{{{U_{0RL}}}}{{{Z_{RL}}}} = \frac{{\sqrt {U_{0R}^2 + U_{0L}^2} }}{{\sqrt {R_{}^2 + Z_L^2} }} = \frac{{{U_{0R}}}}{U} = \frac{{{U_{0L}}}}{{{Z_L}}} = \sqrt 2 I\end{array} \right.\)

Điện áp nhanh pha hơn dòng điện góc φ, xác định từ biểu thức \(\left[ \begin{array}{l}\tan \phi  = \frac{{{U_L}}}{{{U_R}}} = \frac{{{Z_L}}}{R}\\\cos \phi  = \frac{{{U_R}}}{{{U_R}L}} = \frac{R}{{{Z_{RL}}}} = \frac{R}{{\sqrt {{R^2} + Z_L^2} }}\end{array} \right.\)

Giản đồ véc tơ: 

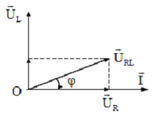
Khi đó: j_u = j_i + j

Chú ý: Để viết biểu thức của u, u_L, u_R trong mạch RL thì ta cần phải xác định được pha của i, rồi tính toán các pha theo quy tắc \(\left\{ \begin{array}{l}{\phi _{{u_L}}} = {\phi _i} + \frac{\pi }{2}\\{\phi _{{u_R}}} = {\phi _i}\end{array} \right.\)

II. MẠCH ĐIỆN XOAY CHIỀU GỒM R, C

Đặc điểm:

Điện áp và tổng trở của mạch: \(\left\{ \begin{array}{l}{U_{RC}} = \sqrt {U_R^2 + U_C^2} \\{Z_{RC}} = \sqrt {{R^2} + Z_C^2} \end{array} \right.\)

Định luật Ohm cho đoạn mạch: \(\left\{ \begin{array}{l}I = \frac{{{U_{RC}}}}{{{Z_{RC}}}} = \frac{{\sqrt {U_R^2 + U_C^2} }}{{\sqrt {R_{}^2 + Z_C^2} }} = \frac{{{U_R}}}{U} = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{I_0}}}{{\sqrt 2 }}\\{I_0} = \frac{{{U_{0RC}}}}{{{Z_{RC}}}} = \frac{{\sqrt {U_{0R}^2 + U_{0C}^2} }}{{\sqrt {R_{}^2 + Z_C^2} }} = \frac{{{U_{0R}}}}{U} = \frac{{{U_{0C}}}}{{{Z_C}}} = \sqrt 2 I\end{array} \right.\)

Điện áp chậm pha hơn dòng điện góc φ, xác định từ biểu thức: \(\tan \phi  =  - \frac{{{U_C}}}{{{U_R}}} =  - \frac{{{Z_C}}}{R}\); j = j_u - j_i

Giản đồ véc tơ:

Chú ý: Để viết biểu thức của u, u_C, u_R trong mạch RC thì ta cần phải xác định được pha của i, rồi tính toán các pha theo quy tắc \(\left\{ \begin{array}{l}{\phi _{{u_C}}} = {\phi _i} - \frac{\pi }{2}\\{\phi _{{u_R}}} = {\phi _i}\end{array} \right.\)

III. MẠCH ĐIỆN XOAY CHIỀU GỒM L, C

Đặc điểm:

     Điện áp và tổng trở của mạch: \(\left\{ \begin{array}{l}{U_C} = \left| {{U_L} - {U_C}} \right|\\{Z_C} = \left| {{Z_L} - {Z_C}} \right|\end{array} \right.\) à \(\left\{ \begin{array}{l}I = \frac{{{U_{LC}}}}{{{Z_{LC}}}} = \frac{{\left| {{U_L} - {U_C}} \right|}}{{\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{I_0}}}{{\sqrt 2 }}\\{I_0} = \frac{{{U_{0LC}}}}{{{Z_{LC}}}} = \frac{{\left| {{U_{0L}} - {U_{0C}}} \right|}}{{\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U_{0L}}}}{{{Z_L}}} = \frac{{{U_{0C}}}}{{{Z_C}}} = I\sqrt 2 \end{array} \right.\)

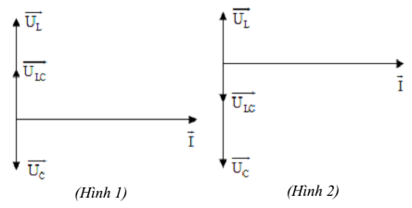
* Giản đồ véc tơ:

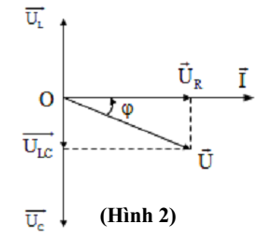
     - Khi U_L > U_C hay Z_L > Z_C thì u_LC nhanh pha hơn i góc π/2. (Hình 1). Khi đó ta nói mạch có tính cảm kháng.

     - Khi U_L < U_C hay Z_L < Z_C thì u_LC chậm pha hơn i góc π/2. (Hình 2). Khi đó ta nói mạch có tính dung kháng.

BÀI GIẢNG MẠCH ĐIỆN XOAY CHIỀU RLC - PHẦN 1

I. MẠCH ĐIỆN XOAY CHIỀU RLC NỐI TIẾP

Đặc điểm:

Điện áp và tổng trở của mạch: \(\left\{ \begin{array}{l}U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}}  \to {U_0} = \sqrt {U_{0R}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} \\Z = \sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \end{array} \right.\)

Định luật Ohm cho mạch: \(\left\{ \begin{array}{l}I = \frac{U}{Z} = \frac{{\sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} }}{{\sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{{U_R}}}{R} = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{I_0}}}{{\sqrt 2 }}\\{I_0} = \frac{{{U_0}}}{Z} = \frac{{\sqrt {U_{0R}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} }}{{\sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{{U_{0R}}}}{R} = \frac{{{U_{0L}}}}{{{Z_L}}} = \frac{{{U_{0C}}}}{{{Z_C}}} = I\sqrt 2 \end{array} \right.\)

Độ lệch pha của điện áp và cường độ dòng điện trong mạch là φ, được cho bởi \(\tan \phi  = \frac{{{U_L} - {U_C}}}{{{U_R}}} = \frac{{{Z_L} - {Z_C}}}{R}\);j = j_u- j_i

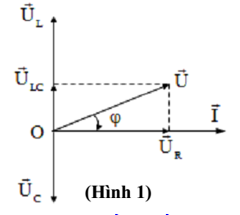
- Khi U_L > U_C hay Z_L > Z_C thì u nhanh pha hơn i góc φ. (Hình 1). Khi đó ta nói mạch có tính cảm kháng.

- Khi U_L < U_C hay Z_L < Z_C thì u chậm pha hơn i góc φ. (Hình 2). Khi đó ta nói mạch có tính dung gháng.

 Giản đồ véc tơ:

II. CỘNG HƯỞNG ĐIỆN TRONG MẠCH RLC NỐI TIẾP

* Khái niệm về cộng hưởng điện

Khi Z_L = Z_C Û wL = \[\] Û w² = \[\] à w = \[\] thì trong mạch có xảy ra hiện tượng cộng hưởng điện.

* Đặc điểm của hiện tượng cộng hưởng điện

     + Khi xảy ra hiện tượng cộng hưởng điện thì tổng trở của mạch đạt giá trị nhỏ nhất, Z_min = R cường độ hiệu dụng của dòng điện đạt giá trị cực đại với I_max= \[\] .

     + Điện áp giữa hai đầu điện trở R bằng với điện áp hai đầu mạch, U_R = U.

     + Cường độ dòng điện trong mạch cùng pha với điện áp hai đầu mạch

     + Các điện áp giữa hai đầu tu điện và hai đầu cuộn cảm có cùng độ lớn (tức U_L = U_C) nhưng ngược pha nên triệt tiêu nhau.

     + Điều kiện cộng hưởng điện ω = \[\] à \(f = \frac{1}{{2\pi \sqrt {LC} }}\) à w²LC = 1

Chú ý: Khi đang xảy ra cộng hưởng thì tổng trở của mạch đạt cực tiểu, cường độ dòng điện đạt cực đại. Nếu ta tăng hay giảm tần số dòng điện thì tổng trở của mạch sẽ tăng, đồng thời cường độ dòng điện sẽ giảm.

BÀI GIẢNG MẠCH ĐIỆN XOAY CHIỀU RLC - PHẦN 2

II. MẠCH ĐIỆN RLC NỐI TIẾP KHI CUỘN DÂY CÓ THÊM ĐIỆN TRỞ r

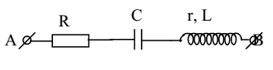
Cho mạch điện xoay chiều RLC trong đó cuộn dây không thuẩn cảm mà có thêm một điện trở r

     Khi đó R và r được gọi là tổng trở thuần của mạch và do R, r nối

tiếp nên tổng trở thuần kí hiệu là R₀ = R + r à U_R0 = U_R + U_r

Đặc điểm của mạch điện:

 Điện áp và tổng trở của mạch\(\left\{ \begin{array}{l}U = \sqrt {U_{{R_0}}^2 + {{\left( {{U_L} - {U_C}} \right)}^2}}  = \sqrt {{{({U_R} + {U_r})}^2} + {{\left( {{U_L} - {U_C}} \right)}^2}} \\Z = \sqrt {R_0^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}}  = \sqrt {{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \end{array} \right.\)

Định luật Ôm \(I = \frac{U}{Z} = \frac{{\sqrt {U_{{R_0}}^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} }}{{\sqrt {R_0^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{{U_R}}}{R} = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{U_r}}}{r} = \frac{{{I_0}}}{{\sqrt 2 }}\)

 Độ lệch pha của điện áp và cường độ dòng điện trong mạch là φ, được cho bởi hệ thức

\(\left\{ \begin{array}{l}\tan \phi  = \frac{{{U_L} - {U_C}}}{{{U_{{R_0}}}}} = \frac{{{U_L} - {U_C}}}{{{U_R} + {U_r}}} = \frac{{{Z_L} - {Z_C}}}{{R + r}},\phi  = {\phi _u} - {\phi _i}\\\sin \phi  = \frac{{{U_L} - {U_C}}}{U}\end{array} \right.\)

Nhận xét :

     Cuộn dây có thêm điện trở hoạt động r nên có thể coi như một mạch điện (r, L) thu nhỏ. Các công thức tính toán với cuộn dây cũng như tính toán với đoạn mạch RL đã khảo sát ở trên:

- Điện áp hai đầu cuộn dây U_d = U_Lr = \(\sqrt {U_r^2 + U_L^2} \)

- Tổng trở của cuộn dây Z_d = Z_Lr =\(\sqrt {r_{}^2 + Z_L^2} \)

- Độ lệch pha của u_d và i được cho bởi tanφ_d = \[\] à điện áp u_d nhanh pha hơn i góc φ_d hay φ_d = φ_ud – φ_i

Chú ý : Trong một số bài toán mà khi đề bài cho “nhập nhằng” không biết được cuộn dây có thuẩn cảm hay không hoặc đôi khi yêu cầu chứng minh rằng cuộn dây có thêm điện trở hoạt động r thì ta làm theo cách sau:

     - Giả sử rằng cuộn dây không có điện trở hoạt động, r = 0.

     - Thiết lập các biểu thức với r = 0 thì sẽ mâu thuẫn với giả thiết cho.

     - Kết luận là cuộn dây phải có điện trở hoạt động r ≠ 0.

CÁC LOẠI MẠCH ĐIỆN XOAY CHIỀU

I. MẠCH ĐIỆN CHỈ CÓ ĐIỆN TRỞ THUẦN R

Đặc điểm:

* Điện áp và dòng điện trong mạch cùng pha với nhau (tức φ_u = φ_i): \(\left\{ \begin{array}{l}{u_R} = {U_{0R}}\cos (\omega t) = {U_R}\sqrt 2 \cos (\omega t)\\i = {I_0}\cos (\omega t)\end{array} \right.\)

* Định luật Ohm cho mạch: \(\left\{ \begin{array}{l}i = \frac{{{u_R}}}{R}\\{I_0} = \frac{{{U_{0R}}}}{R} \to I = \frac{{{U_R}}}{R}\end{array} \right.\)

* Giản đồ véc tơ:

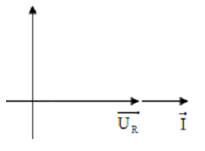
* Đồ thị của u_R theo i (hoặc ngược lại) có dạng đường thẳng đi qua gốc tọa độ.

* Nhiệt lượng tỏa ra trên điện trở R trong thời gian t là: Q = I²Rt = \(\frac{{I_0^2Rt}}{2}\)

* Nếu hai điện trở R₁ và R₂ ghép nối tiếp thì ta có công thức R = R₁ + R₂, ngược lại hai điện trở mắc song song thì \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\)

II. MẠCH ĐIỆN CHỈ CÓ CUỘN CẢM THUẦN VỚI ĐỘ TỰ CẢM L

Đặc điểm:

* Điện áp nhanh pha hơn dòng điện góc π/2 (tức φ_u = φ_i + π/2): \(\left\{ \begin{array}{l}{u_L} = {U_L}\cos (\omega t) = {U_L}\sqrt 2 \cos (\omega t)\\i = {I_0}\cos (\omega t - \frac{\pi }{2})\end{array} \right.\)

* Cảm kháng của mạch: Z_L = ωL = 2πf.L à Đồ thị của cảm kháng theo L là đường thẳng đi qua gốc tọa độ (dạng y = ax).

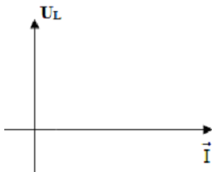
* Định luật Ohm cho mạch \(\left\{ \begin{array}{l}{I_0} = \frac{{{U_{0L}}}}{{{Z_L}}} = \frac{{{U_{0L}}}}{{L.\omega }} = \frac{{{U_{0L}}}}{{2\pi fL}}\\I = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{U_L}}}{{L.\omega }} = \frac{{{U_{0L}}}}{{\sqrt 2 {Z_L}}} = \frac{{{U_{0L}}}}{{\sqrt 2 \omega L}}\end{array} \right.\)

 Giản đồ véc tơ:

* Do u_L nhanh pha hơn i góc π/2 nên ta có phương trình liên hệ của u_L và i độc lập với thời gian

\(\left\{ \begin{array}{l}{u_L} = {U_{0L}}\cos (\omega t)\\i = {I_0}\cos (\omega t - \frac{\pi }{2}) = {I_0}\sin (\omega t)\end{array} \right.\) Þ \({\left( {\frac{{{u_L}}}{{{U_{0L}}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\)

Từ hệ thức trên ta thấy đồ thị của u_L theo i (hoặc ngược lại) là đường elip

Hệ quả:

Tại thời điểm t₁ điện áp và dòng điện có giá trị là u₁; i₁, tại thời điểm t₂ điện áp và dòng điện có giá trị là u₂; i₂ thì ta có

 \({\left( {\frac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{{i_1}}}{{{I_0}}}} \right)^2}\)= 1 = \({\left( {\frac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{{i_2}}}{{{I_0}}}} \right)^2}\) à \(\frac{{u_1^2 - u_2^2}}{{U_0^2}} = \frac{{i_2^2 - i_1^2}}{{I_0^2}}\) Û \(\frac{{{U_0}}}{{{I_0}}} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \)à\(\left\langle \begin{array}{l}{Z_L} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \\L.\omega  = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \end{array} \right.\)

III. MẠCH ĐIỆN CHỈ CÓ TỤ ĐIỆN VỚI ĐIỆN DUNG C

Đặc điểm:

* Điện áp chậm pha hơn dòng điện góc π/2 (tức φ_u = φ_i - π/2): \(\left\{ \begin{array}{l}{u_C} = {U_{0C}}\cos (\omega t) = {U_C}\sqrt 2 \cos (\omega t)\\i = {I_0}\cos (\omega t + \frac{\pi }{2})\end{array} \right.\)

 * Dung kháng của mạch: Z_C = \[\] =  à Đồ thị của dung kháng theo C là đường cong hupebol (dạng y = \[\] ).

* Định luật Ohm cho mạch \(\left\{ \begin{array}{l}{I_0} = \frac{{{U_{0C}}}}{{{Z_C}}} = \frac{{{U_{0C}}}}{{\frac{1}{{C.\omega }}}} = \omega C{U_{0C}}\\I = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{U_C}}}{{\frac{1}{{C\omega }}}} = \omega C{U_C} = \frac{{{U_{0L}}}}{{\sqrt 2 {Z_C}}} = \frac{{\omega C{U_{0C}}}}{{\sqrt 2 }}\end{array} \right.\)

 Giản đồ véc tơ:

* Do u_C chậm pha hơn i góc π/2 nên ta có phương trình liên hệ của u_L và i độc lập với thời gian

\(\left\{ \begin{array}{l}{u_C} = {U_{0C}}\cos (\omega t)\\i = {I_0}\cos (\omega t + \frac{\pi }{2}) =  - {I_0}\sin (\omega t)\end{array} \right.\) Þ \({\left( {\frac{{{u_C}}}{{{U_{0C}}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\)

Từ hệ thức trên ta thấy đồ thị của u_C theo i (hoặc ngược lại) là đường elip

Hệ quả:

Tại thời điểm t₁ điện áp và dòng điện có giá trị là u₁; i₁, tại thời điểm t₂ điện áp và dòng điện có giá trị là u₂; i₂ thì ta có

 \({\left( {\frac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{{i_1}}}{{{I_0}}}} \right)^2}\)= 1 = \({\left( {\frac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\frac{{{i_2}}}{{{I_0}}}} \right)^2}\) à \(\frac{{u_1^2 - u_2^2}}{{U_0^2}} = \frac{{i_2^2 - i_1^2}}{{I_0^2}}\) Û \(\frac{{{U_0}}}{{{I_0}}} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \)à\(\left\langle \begin{array}{l}{Z_C} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \\\frac{1}{{C.\omega }} = \sqrt {\frac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \end{array} \right.\)

BÀI GIẢNG CÔNG SUẤT CỦA MẠCH ĐIỆN XOAY CHIỀU

I. CÔNG SUẤT MẠCH ĐIỆN XOAY CHIỀU

1) Biểu thức của công suất

     Cho mạch điện xoay chiều có biểu thức điện áp và dòng điện \(\left\{ \begin{array}{l}u = {U_0}\cos (\omega t + {\phi _u})V = U\sqrt 2 \cos (\omega t + {\phi _u})V\\i = {I_0}\cos (\omega t + {\phi _i})A = I\sqrt 2 \cos (\omega t + {\phi _i})A\end{array} \right.\)

     Công suất của mạch được cho bởi P = UIcosφ, với φ = φ_u – φ_i là độ lệch pha của u và i.

Chú ý: Khi tính toán công suất tiêu thụ của đoạn mạch điện xoay chiều thì ta phải chuyển đổi các phương trình của

u và i về cùng dạng với nhau theo quy tắc sinx = cos(x - p/2)

2) Điện năng tiêu thụ của mạch điện

     Điện năng tiêu thụ của mạch điện là W = P.t, với t là thời gian dòng điện chạy trong mạch, đơn vị giây, (s).

II. HỆ SỐ CÔNG SUẤT

1) Khái niệm hệ số công suất

     Đại lượng cosφ trong công thức tính công suất P = UIcosφ được gọi là hệ số công suất của mạch điện xoay chiều.

2) Công thức tính hệ số công suất

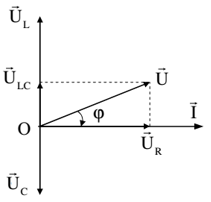
a) Theo khái niệm hệ số công suất ta có cosφ = \[\] = \(\frac{{2P}}{{{U_0}{I_0}}}\)

b) Theo giản đồ ta có cosφ = \(\frac{{{U_R}}}{U} = \frac{R}{Z}\)(*)

(*) là công thức tính giá trị của hệ số công suất trong các bài toán

thường gặp.

3) Biểu thức tính công suất khi mạch có R

     Ta có P = UIcosφ = UI.\[\] = \[\].IR = I².R

III. CÔNG SUẤT, HỆ SỐ CÔNG SUẤT CỦA MỘT SỐ LOẠI ĐOẠN MẠCH ĐIỆN THƯỜNG GẶP

Chú ý:

- Công suất P = UIcosφ là công suất tiêu thụ trên toàn mạch điện, còn công suất P = I²R là công suất tỏa nhiệt khi mạch có điện trở R, một phần công suất của mạch bị hao phí dưới dạng công suất tỏa nhiệt còn phần lớn là công suất có ích, khi đó P = P_{có ích} + P_{hao phí} Û Uicosφ = P_{có ích} + I ²R

     Mà I = \[\] à P_{hao phí} = \({\left( {\frac{P}{{U\cos \phi }}} \right)^2}R\)

Từ công thức tính công suất hao phí trên cho thấy để làm giảm đi công suất hao phí thì người ta tìm cách nâng cao hệ số công suất. Và trong thực tế thì không sử dụng những thiết bị mà có hệ số công suất cosφ < 0,85.

- Hiệu suất của mạch điện (thiết bị tiêu thụ điện) là H = \(\frac{{{P_{c\'o \,\'i ch}}}}{P}.100\% \)

CỰC TRỊ TRONG MẠCH ĐIỆN XOAY CHIỀU - PHẦN 1

Nguyên tắc chung thiết lập các biểu thức tìm cực trị trong mạch điện xoay chiều:

     Để tìm cực trị của một biểu thức nào đó thì chúng ta xuất phát từ công thức tổng quát của chúng, thực hiện các phép biến đổi theo quy tắc nếu tử số và mẫu số đều là đại lượng biến thiên thì chỉ để một biểu thức thay đổi (chia cả tử và mẫu cho tử số chẳng hạn..)

Bổ đề :

     Bất đẳng thức Cauchy : Cho hai số không âm a, b khi đó \(\frac{{a + b}}{2} \ge \sqrt {ab} \) Û a + b ³ 2\[\sqrt[]{{ab}}\]

     Dấu bằng xảy ra khi a = b.

      Hàm số bậc hai y = ax² + bx + c, với a > 0 đạt giá trị nhỏ nhất tại điểm x = - \[\]; y_min = - \[\] = - \[\]

I. MẠCH RLC CÓ R THAY ĐỔI

BÀI TOÁN TỔNG QUÁT 1:

Cho mạch điện xoay chiều RLC trong đó R có thể thay đổi được (R còn được gọi là biến trở). Tìm giá trị của R để

a) cường độ hiệu dụng I của mạch đạt giá trị cực đại.

b) điện áp hiệu dụng hai đầu L hoặc C đạt cực đại.

c) công suất tỏa nhiệt trên R là P₀ cho trước.

d) công suất tỏa nhiệt trên điện trở R đạt cực đại.

e) điện áp giữa hai đầu đoạn mạch RL, RC đạt cực đại, cực tiểu (nếu có)

Hướng dẫn giải:

 a) Cường độ hiệu dụng I = \[\] = \(\frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\) à I_max Û R = 0

     Vậy R = 0 thì I_max và giá trị I_max =\(\frac{U}{{\left| {{Z_L} - {Z_C}} \right|}}\)

 b) Ta có U_L = I.Z_L. Do L không đổi nên (U_L)_max khi I_max Û R = 0.

     Khi đó, U_{L max} = I_max.L = \(\frac{{U.{Z_L}}}{{\left| {{Z_L} - {Z_C}} \right|}}\)

     Tương tự ta cũng có \(\left\{ \begin{array}{l}{U_{C\max }} \leftrightarrow R = 0\\{U_{C\max }} = {I_{\max }}.{Z_C} = \frac{{U.{Z_C}}}{{\left| {{Z_L} - {Z_C}} \right|}}\end{array} \right.\)

 c) Theo bài ta có P = P₀ Û I²R = P₀ Û \(\frac{{{U^2}}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}.R\)= P₀ Þ P₀R² - U²R + P₀(Z_L-Z_C)² = 0

     Thay các giá trị của U, Z_L, Z_C và P₀ vào phương trình trên ta giải được R cần tìm.

d) Công suất tỏa nhiệt trên R:

P = I²R = \(\frac{{{U^2}}}{{{Z^2}}}.R\) = \(\frac{{{U^2}}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}.R\)= \(\frac{{{U^2}}}{{R + \frac{{{{({Z_L} - {Z_C})}^2}}}{R}}} \le \frac{{{U^2}}}{{2\sqrt {R.\frac{{{{({Z_L} - {Z_C})}^2}}}{R}} }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}}\)

 Dấu bằng xảy ra khi \(R = \frac{{{{({Z_L} - {Z_C})}^2}}}{R}\) Þ R = |Z_L - Z_C| và P_max = \(\frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}}\)=\(\frac{{{U^2}}}{{2R}}\)

Vậy mạch RLC có R thay đổi, giá trị của R và P_max tương ứng là \(\left\{ \begin{array}{l}R = |{Z_L} - {Z_C}|\\{P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2R}}\end{array} \right.\)

Chú ý:

     * Trong trường hợp P_max thì hệ số công suất của mạch khi đó là cosφ = \[\] =\(\frac{R}{{\sqrt {{R^2} + {R^2}} }} = \frac{1}{{\sqrt 2 }}\), do R= |Z_L - Z_C| . Tức là độ lệch pha của u và i khi đó là π/4.

      * Khi cuộn dây có thêm điện trở hoạt động r ≠ 0 thì ta còn có thêm dạng bài tính công suât tỏa nhiệt trên R, trên cuộn dây và trên toàn mạch.

TH1: Công suất tỏa nhiệt trên toàn mạch cực đại

P = I²(R+r) = \(\frac{{{U^2}}}{{{Z^2}}}.(R + r)\) = \(\frac{{{U^2}}}{{{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}}}.(R + r)\) = \(\frac{{{U^2}}}{{(R + r) + \frac{{{{({Z_L} - {Z_C})}^2}}}{{R + r}}}} \le \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}}\)

     Từ đó ta cũng được giá trị của R và P_max tương ứng: \(\left\{ \begin{array}{l}R + r = |{Z_L} - {Z_C}|\\{P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}}\end{array} \right. \leftrightarrow \left\{ \begin{array}{l}R = |{Z_L} - {Z_C}| - r\\{P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}}\end{array} \right.\)

TH2: Công suất tỏa nhiệt trên R cực đại

P = I²R = \(\frac{{{U^2}}}{{{Z^2}}}.R\) = \(\frac{{{U^2}}}{{{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}}}.R\) = \(\frac{{{U^2}}}{{\frac{{({R^2} + 2Rr + {r^2})}}{R} + \frac{{{{({Z_L} - {Z_C})}^2}}}{R}}} \le \frac{{{U^2}}}{{R + 2r + \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R}}}\)

 Áp dụng BĐT Cauchy cho mẫu số ta cũng được

P_R £ \(\frac{{{U^2}}}{{2r + \sqrt {R.\frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R}} }} \le \frac{{{U^2}}}{{2r + \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} }}\)

     Từ đó ta cũng được giá trị của R và (P_R)max tương ứng: \(\left\{ \begin{array}{l}R = \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} \\{({P_R})_{\max }} = \frac{{{U^2}}}{{2r + \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} }}\end{array} \right.\)

BÀI TOÁN TỔNG QUÁT 2:

Cho mạch điện RLC có R thay đổi. Điện áp hiệu dụng hai đầu mạch điện là U. Khi R = R₁ và R = R₂ thì mạch tiêu thụ cùng một công suất (hay P₁ = P₂). Chứng minh rằng:

a) R₁.R₂= (Z_L- Z_C)²

b) |φ₁| + |φ₂| = , với φ₁, φ₂ lần lượt là độ lệch pha của u và i khi R = R₁, R = R₂.

c) Công suất tỏa nhiệt tương ứng khi đó P₁ = P₂ = \(\frac{{{U^2}}}{{{R_1} + {R_2}}}\)

Hướng dẫn giải

a) Theo giả thiết ta có P₁ = P₂

Û\(\frac{{{U^2}}}{{R_1^2 + {{({Z_L} - {Z_C})}^2}}}.{R_1} = \frac{{{U^2}}}{{R_2^2 + {{({Z_L} - {Z_C})}^2}}}.{R_2}\)

         Û\({R_1}.\left( {R_2^2 + {{({Z_L} - {Z_C})}^2}} \right) = {R_2}.\left( {R_1^2 + {{({Z_L} - {Z_C})}^2}} \right)\) Û \({R_1}R_2^2 + {R_1}{({Z_L} - {Z_C})^2} = {R_2}R_1^2 + {R_2}{({Z_L} - {Z_C})^2}\)

 Û \({R_1}R_2^{}({R_1} + R_2^{}) = {({Z_L} - {Z_C})^2}({R_2} - {R_2})\) Û R₁R₂ = (Z_L - Z_C)²

b) Ta có \(\left\{ \begin{array}{l}\tan \left| {{\phi _1}} \right| = \frac{{\left| {{Z_L} - {Z_C}} \right|}}{{{R_1}}}\\\tan \left| {{\phi _2}} \right| = \frac{{\left| {{Z_L} - {Z_C}} \right|}}{{{R_2}}}\end{array} \right.\) do R₁R₂ = (Z_L - Z_C)² Þ \(\frac{{\left| {{Z_L} - {Z_C}} \right|}}{{{R_1}}} = \frac{{{R_2}}}{{\left| {{Z_L} - {Z_C}} \right|}}\) à tan|j₁| = cot|j₂|

     Từ đó ta được |j₁| + |j2| = à đpcm

c) Ta có P = P₁ = P₂ = I\(_1^2\).R Û \(P = \frac{{{U^2}}}{{R_1^2 + {{({Z_L} - {Z_C})}^2}}}.{R_1} = \frac{{{U^2}}}{{R_1^2 + {R_1}{R_2}}}.{R_1} = \frac{{{U^2}}}{{R_1^{} + {R_2}}}\) à đpcm

     Vậy mạch RLC có R thay đổi mà R = R₁ và R = R₂ thì P₁ = P₂ sẽ thỏa mãn \(\left\{ \begin{array}{l}{R_1}{R_2} = {({Z_L} - {Z_C})^2}\\\left| {{\phi _1}} \right| + \left| {{\phi _2}} \right| = \frac{\pi }{2}\\P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\end{array} \right.\)

Chú ý:

* Trong trường hợp mạch điện bị khuyết một phần tử (hoặc L hoặc C) thì ta có các điều kiện tương tự

     + Với mạch R, L: \(\left\{ \begin{array}{l}{R_1}{R_2} = {Z_L}^2\\P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\end{array} \right.\)

     + Với mạch R, C: \(\left\{ \begin{array}{l}{R_1}{R_2} = {Z_C}^2\\P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\end{array} \right.\)

* Các em cần phân biệt rõ hai trường hợp công suất cực đại khi R biến thiên và công suất bằng nhau.

     + Khi R biến thiên thì công suất cực đại là \({P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2R}}\)

      + Khi R biến thiên có hai giá trị cho P bằng nhau thì

\(\left\{ \begin{array}{l}{R_1}{R_2} = {({Z_L} - {Z_C})^2}\\P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\end{array} \right.\)à \({P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2\sqrt {{R_1}{R_2}} }}\)

BÀI GIẢNG CỰC TRỊ TRONG MẠCH ĐIỆN XOAY CHIỀU - PHẦN 2

II. MẠCH RLC CÓ L THAY ĐỔI

BÀI TOÁN TỔNG QUÁT:

Cho mạch điện xoay chiều RLC trong đó L có thể thay đổi được. Tìm giá trị của L để

a) cường độ hiệu dụng I của mạch đạt giá trị cực đại.

b) công suất tỏa nhiệt của mạch đạt cực đại. Tính giá trị P_max.

c) hệ số công suất của mạch bằng k cho trước.

d) công suất tiêu thụ của mạch là P₀ cho trước.

e) điện áp hiệu dụng hai đầu L đạt cực đại.

f) điện áp hiệu dụng giữa hai đầu đoạn mạch RL cực đại.

Hướng dẫn giải:

a) Ta có I = \[\] = \(\frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\) à I_max Þ Z_min Þ Z_L - Z_C = 0 Û L = \(\frac{1}{{{\omega ^2}C}}\)

 Vậy L = \(\frac{1}{{{\omega ^2}C}}\)thì I_max và giá trị I_max = \[\]

b) Công suất tỏa nhiệt trên mạch P = I²R. Do R không đổi nên P_max khi I_maxL à L = \(\frac{1}{{{\omega ^2}C}}\)

Từ đó P_max = \(I_{\max }^2.R\)= \(\frac{{{U^2}}}{R}\)

c) Ta có k = cosφ = \[\] =\(\frac{R}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\) Û \({R^2} + {({Z_L} - {Z_C})^2} = {\left( {\frac{R}{k}} \right)^2} \Rightarrow \left| {{Z_L} - {Z_C}} \right| = ....\)

d) P₀ = I²R Û P₀ = \(\frac{{{U^2}}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}\) à\({({Z_L} - {Z_C})^2} = \frac{{{U^2}}}{{{P_0}}} - {R^2} \Rightarrow {Z_L} - {Z_C} =  \pm \sqrt {\frac{{{U^2}}}{{{P_0}}} - {R^2}} \) Þ Z_L = ...

 e) U_L = I.Z_L = \[\].Z_L = \(\frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}{Z_L}\)= \(\frac{U}{{\sqrt {\frac{{{R^2}}}{{Z_L^2}} + {{\left( {\frac{{{Z_L} - {Z_C}}}{{{Z_L}}}} \right)}^2}} }}\)=\(\frac{U}{{\sqrt {\frac{{{R^2}}}{{Z_L^2}} + {{\left( {1 - \frac{{{Z_C}}}{{{Z_L}}}} \right)}^2}} }}\)= \(\frac{U}{{\sqrt y }}\)

      Þ (U_L)_max Û y_min

Với y = \(\frac{{{R^2}}}{{Z_L^2}} + {\left( {1 - \frac{{{Z_C}}}{{{Z_L}}}} \right)^2}\), đặt \(\frac{1}{{{Z_L}}} = x\) à y = R²x² + (1-Z_C.x)² = (R² + \(Z_C^2\))x² - 2Z_C.x + 1 º ax²+ bx + c

 Do hệ số a = (R² + \(Z_C^2\)) > 0 à y_min khi x = -  = \(\frac{{ - 2{Z_C}}}{{2({R^2} + Z_C^2)}}\) Û \(\frac{1}{{{Z_L}}} = \)\(\frac{{{Z_C}}}{{{R^2} + Z_C^2}}\) à Z_L = \(\frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)

 Khi đó y = - \[\] = - \[\] = -\(\frac{{Z_C^2 - ({R^2} + Z_C^2)}}{{{R^2} + Z_C^2}}\)= \(\frac{{{R^2}}}{{{R^2} + Z_C^2}}\)à \({\left( {{U_L}} \right)_{\max }} = \frac{U}{{\sqrt {{y_{\min }}} }} = \)\(\frac{U}{{\sqrt {\frac{{{R^2}}}{{{R^2} + Z_C^2}}} }} = \frac{U}{R}\sqrt {{R^2} + Z_C^2} \)

Vậy \({\left( {{U_L}} \right)_{\max }} = \)\(\frac{U}{R}\sqrt {{R^2} + Z_C^2} \) khi Z_L = \(\frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)

Chú ý:

- Khi L = L₁ hoặc L = L₂ mà công suất P (hoặc cường độ hiệu dụng I) không đổi thì ta có Z_C = \(\frac{{{Z_{{L_1}}} + {Z_{{L_2}}}}}{2}\)

- Khi U_L cực đại thì ta có \(\left( {{U_L}} \right)_{\max }^2 = {U^2} + U_R^2 + U_C^2\)

- Khi U_L cực đại thì điện áp hai đầu đoạn mạch RC vuông pha với điện áp u của hai đầu mạch.

- Khi L = L₁ hoặc L = L₂ mà U_L không đổi, đồng thời khi L = L₀ mà U_L đạt cực đại thì ta có hệ thức liên hệ giữa các đại lượng là \(\frac{2}{{{L_0}}} = \frac{1}{{{L_1}}} + \frac{1}{{{L_2}}}\) (*).

Chứng minh (*):

 \({U_{{L_1}}} = {U_{{L_2}}} \Leftrightarrow {I_1}{Z_{{L_1}}} = {I_2}{Z_{{L_2}}}\) Û \(\frac{{{Z_{{L_1}}}}}{{\sqrt {{R^2} + {{({Z_{{L_1}}} - {Z_C})}^2}} }} = \frac{{{Z_{{L_2}}}}}{{\sqrt {{R^2} + {{({Z_{L2}} - {Z_C})}^2}} }}\)

 Û \({R^2}(Z_{{L_1}}^2 - Z_{{L_2}}^2) = Z_{{L_2}}^2{({Z_{{L_1}}} - {Z_C})^2} - Z_{{L_1}}^2{({Z_{{L_2}}} - {Z_C})^2}\)

 Û \({R^2}(Z_{{L_1}}^{} - Z_{{L_2}}^{})(Z_{{L_1}}^{} + Z_{{L_2}}^{}) = \left[ {Z_{{L_2}}^{}({Z_{{L_1}}} - {Z_C}) - Z_{{L_1}}^{}({Z_{{L_2}}} - {Z_C})} \right]\left[ {Z_{{L_2}}^{}({Z_{{L_1}}} - {Z_C}) + Z_{{L_1}}^{}({Z_{{L_2}}} - {Z_C})} \right]\)

 Û \({R^2}(Z_{{L_1}}^{} - Z_{{L_2}}^{})(Z_{{L_1}}^{} + Z_{{L_2}}^{}) = Z_C^{}({Z_{{L_1}}} - {Z_{{L_2}}})\left[ {2Z_{{L_1}}^{}Z_{{L_2}}^{} - {Z_C}({Z_{{L_1}}} + {Z_{{L_2}}})} \right]\)

 Û \({R^2} = \frac{{Z_C^{}({Z_{{L_1}}} - {Z_{{L_2}}})\left[ {2Z_{{L_1}}^{}Z_{{L_2}}^{} - {Z_C}({Z_{{L_1}}} + {Z_{{L_2}}})} \right]}}{{(Z_{{L_1}}^{} - Z_{{L_2}}^{})(Z_{{L_1}}^{} + Z_{{L_2}}^{})}}\)=\(\frac{{Z_C^{}\left[ {2Z_{{L_1}}^{}Z_{{L_2}}^{} - {Z_C}({Z_{{L_1}}} + {Z_{{L_2}}})} \right]}}{{(Z_{{L_1}}^{} + Z_{{L_2}}^{})}}\)

 Û \({R^2} = Z_C^{}\left( {\frac{{2Z_{{L_1}}^{}Z_{{L_2}}^{}}}{{(Z_{{L_1}}^{} + Z_{{L_2}}^{})}} - {Z_C}} \right)\) à\({R^2} + Z_C^2 = Z_C^{}\frac{{2Z_{{L_1}}^{}Z_{{L_2}}^{}}}{{Z_{{L_1}}^{} + Z_{{L_2}}^{}}}\)

Từ đó ta được \(\frac{{{R^2} + Z_C^2}}{{Z_C^{}}} = \frac{{2Z_{{L_1}}^{}Z_{{L_2}}^{}}}{{Z_{{L_1}}^{} + Z_{{L_2}}^{}}}\)

 Khi L = L₀ mà U_L đạt cực đại thì \({Z_{{L_0}}} = \frac{{{R^2} + Z_C^2}}{{Z_C^{}}}\) Û \({Z_{{L_0}}} = \frac{{2Z_{{L_1}}^{}Z_{{L_2}}^{}}}{{Z_{{L_1}}^{} + Z_{{L_2}}^{}}}\)

 Þ \(\frac{1}{{{Z_{{L_0}}}}} = \frac{{Z_{{L_1}}^{} + Z_{{L_2}}^{}}}{{2Z_{{L_1}}^{}Z_{{L_2}}^{}}}\) Û \(\frac{2}{{{Z_{{L_0}}}}} = \frac{1}{{{Z_{{L_1}}}}} + \frac{1}{{{Z_{{L_2}}}}}\) Û \(\frac{2}{{{L_0}}} = \frac{1}{{{L_1}}} + \frac{1}{{{L_2}}}\)

f) U_RL= I.Z_RL = \(\frac{U}{Z}\sqrt {{R^2} + Z_L^2} \)= \(\frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)= \(\frac{U}{{\frac{{\sqrt {{R^2} + Z_L^2 + Z_C^2 - 2{Z_L}{Z_C}} }}{{\sqrt {{R^2} + Z_L^2} }}}}\)=\(\frac{U}{{\sqrt {1 + \frac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}\)=\(\frac{U}{{\sqrt y }}\)

 Với y = \(1 + \frac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}\), đặt Z_L = x Þ y =\(1 + \frac{{Z_C^2 - 2.x.{Z_C}}}{{{R^2} + {x^2}}}\)

 Ta có y’ = \(\frac{{2.{Z_C}\left( {{x^2} - x.{Z_C} - {R^2}} \right)}}{{{{\left( {{R^2} + {x^2}} \right)}^2}}}\) à y’ = 0 Û \({x^2} - x.{Z_C} - {R^2} = 0\) Û \(\left[ \begin{array}{l}x = \frac{{{Z_C} + \sqrt {Z_C^2 + 4{R^2}} }}{2} = {Z_L}\\x = \frac{{{Z_C} - \sqrt {Z_C^2 + 4{R^2}} }}{2} < 0\end{array} \right.\)

Lập bảng biến thiên ta được y_min Û\(x = \frac{{{Z_C} + \sqrt {Z_C^2 + 4{R^2}} }}{2}\)\

Thay giá trị của x ta được y_min = \(\frac{{4{R^2}}}{{4{R^2} + 2Z_C^2 + 2{Z_C}\sqrt {Z_C^2 + 4{R^2}} }}\)= \(\frac{{4{R^2}}}{{{{\left( {{Z_C} + \sqrt {Z_C^2 + 4{R^2}} } \right)}^2}}}\)

 Þ (U_RL)_max = \(\frac{U}{{\sqrt {{y_{\min }}} }}\)=\(\frac{U}{{\sqrt {\frac{{4{R^2}}}{{{{\left( {{Z_C} + \sqrt {Z_C^2 + 4{R^2}} } \right)}^2}}}} }} = \frac{{U\left( {{Z_C} + \sqrt {Z_C^2 + 4{R^2}} } \right)}}{{2R}}\)\( = \frac{U}{R}.\frac{{{Z_C} + \sqrt {Z_C^2 + 4{R^2}} }}{2}\)=\(U\frac{{{Z_L}}}{R}\)

Vậy khi L biến thiên để (U_RL) _max thì ta có \(\left\{ \begin{array}{l}{Z_L} = \frac{{{Z_C} + \sqrt {Z_C^2 + 4{R^2}} }}{2}\\{\left( {{U_{RL}}} \right)_{\max }} = \frac{{U\left( {{Z_C} + \sqrt {Z_C^2 + 4{R^2}} } \right)}}{{2R}} = U\frac{{{Z_L}}}{R}\end{array} \right.\)

BÀI GIẢNG CỰC TRỊ TRONG MẠCH ĐIỆN XOAY CHIỀU - PHẦN 3

III. MẠCH RLC CÓ C THAY ĐỔI

BÀI TOÁN TỔNG QUÁT:

Cho mạch điện xoay chiều RLC trong đó C có thể thay đổi được. Tìm giá trị của C để

a) cường độ hiệu dụng I của mạch đạt giá trị cực đại.

b) công suất tỏa nhiệt của mạch đạt cực đại. Tính giá trị P_max đó.

c) điện áp hiệu dụng hai đầu C đạt cực đại.

d) điện áp hiệu dụng giữa hai đầu đoạn mạch RC cực đại.

Hướng dẫn giải:

a) Ta có I = \[\] = \(\frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\) à I_max Þ Z_min Þ Z_L - Z_C = 0 Û C = \(\frac{1}{{{\omega ^2}L}}\)

 Vậy C = \(\frac{1}{{{\omega ^2}L}}\)thì I_max và giá trị I_max =  

b) Công suất tỏa nhiệt trên mạch P = I²R. Do R không đổi nên P_max khi I_maxL à C = \(\frac{1}{{{\omega ^2}L}}\)

Từ đó P_max = \(I_{\max }^2.R\)= \(\frac{{{U^2}}}{R}\)

c) U_C = I.Z_C = .Z_C = \(\frac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}{Z_C}\)= \(\frac{U}{{\sqrt {\frac{{{R^2}}}{{Z_C^2}} + {{\left( {\frac{{{Z_L} - {Z_C}}}{{{Z_C}}}} \right)}^2}} }}\)=\(\frac{U}{{\sqrt {\frac{{{R^2}}}{{Z_C^2}} + {{\left( {\frac{{{Z_L}}}{{{Z_C}}} - 1} \right)}^2}} }}\)= \(\frac{U}{{\sqrt y }}\)

      Þ (U_L)_max Û y_min

Với y = \(\frac{{{R^2}}}{{Z_C^2}} + {\left( {\frac{{{Z_L}}}{{{Z_C}}} - 1} \right)^2}\), đặt \(\frac{1}{{{Z_C}}} = x\) à y = R²x² + (1-Z_L.x)² = (R² + \(Z_L^2\))x² - 2Z_L.x + 1 º ax²+ bx + c

 Do hệ số a = (R² + \(Z_L^2\)) > 0 à y_min khi x = - = \(\frac{{ - 2{Z_L}}}{{2({R^2} + Z_L^2)}}\) Û \(\frac{1}{{{Z_C}}} = \)\(\frac{{{Z_L}}}{{{R^2} + Z_L^2}}\) à Z_C = \(\frac{{{R^2} + Z_L^2}}{{{Z_L}}}\)

 Khi đó y = - = - = -\(\frac{{Z_L^2 - ({R^2} + Z_L^2)}}{{{R^2} + Z_L^2}}\)= \(\frac{{{R^2}}}{{{R^2} + Z_L^2}}\)à \({\left( {{U_C}} \right)_{\max }} = \frac{U}{{\sqrt {{y_{\min }}} }} = \)\(\frac{U}{{\sqrt {\frac{{{R^2}}}{{{R^2} + Z_L^2}}} }} = \frac{U}{R}\sqrt {{R^2} + Z_L^2} \)

Vậy \({\left( {{U_C}} \right)_{\max }} = \)\(\frac{U}{R}\sqrt {{R^2} + Z_L^2} \) khi Z_C = \(\frac{{{R^2} + Z_L^2}}{{{Z_L}}}\)

Chú ý:

     - Khi C = C₁ hoặc C = C₂ mà công suất P (hoặc cường độ hiệu dụng I) không đổi thì ta có Z_L = \(\frac{{{Z_{{C_1}}} + {Z_{{C_2}}}}}{2}\)

     - Khi U_C cực đại thì ta có \(\left( {{U_C}} \right)_{\max }^2 = {U^2} + U_R^2 + U_L^2\)

     - Khi U_C cực đại thì điện áp hai đầu đoạn mạch RL vuông pha với điện áp u của hai đầu mạch.

     - Khi C = C₁ hoặc C = C₂ mà U_C không đổi, đồng thời khi C = C₀ mà U_C đạt cực đại thì ta có hệ thức liên hệ giữa các đại lượng là \({C_0} = \frac{{{C_1} + {C_2}}}{2}\)

d) U_RC= I.Z_RC = \(\frac{U}{Z}\sqrt {{R^2} + Z_C^2} \)= \(\frac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)= \(\frac{U}{{\frac{{\sqrt {{R^2} + Z_C^2 + Z_K^2 - 2{Z_L}{Z_C}} }}{{\sqrt {{R^2} + Z_C^2} }}}}\)=\(\frac{U}{{\sqrt {1 + \frac{{Z_L^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_C^2}}} }}\)=\(\frac{U}{{\sqrt y }}\)

 Với y = \(1 + \frac{{Z_L^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_C^2}}\), đặt Z_C = x Þ y =\(1 + \frac{{Z_L^2 - 2.x.{Z_L}}}{{{R^2} + {x^2}}}\)

 Ta có y’ = \(\frac{{2.{Z_L}\left( {{x^2} - x.{Z_L} - {R^2}} \right)}}{{{{\left( {{R^2} + {x^2}} \right)}^2}}}\) à y’ = 0 Û \({x^2} - x.{Z_L} - {R^2} = 0\) Û \(\left[ \begin{array}{l}x = \frac{{{Z_L} + \sqrt {Z_L^2 + 4{R^2}} }}{2} = {Z_C}\\x = \frac{{{Z_L} - \sqrt {Z_L^2 + 4{R^2}} }}{2} < 0\end{array} \right.\)

Lập bảng biến thiên ta được y_min Û\(x = \frac{{{Z_L} + \sqrt {Z_L^2 + 4{R^2}} }}{2}\)\

Thay giá trị của x ta được y_min = \(\frac{{4{R^2}}}{{4{R^2} + 2Z_L^2 + 2{Z_L}\sqrt {Z_L^2 + 4{R^2}} }}\)= \(\frac{{4{R^2}}}{{{{\left( {{Z_L} + \sqrt {Z_L^2 + 4{R^2}} } \right)}^2}}}\)

 Þ (U_RC)_max = \(\frac{U}{{\sqrt {{y_{\min }}} }}\)=\(\frac{U}{{\sqrt {\frac{{4{R^2}}}{{{{\left( {{Z_L} + \sqrt {Z_L^2 + 4{R^2}} } \right)}^2}}}} }} = \frac{{U\left( {{Z_L} + \sqrt {Z_L^2 + 4{R^2}} } \right)}}{{2R}}\)\( = \frac{U}{R}.\frac{{{Z_L} + \sqrt {Z_L^2 + 4{R^2}} }}{2}\)=\(U\frac{{{Z_C}}}{R}\)

Vậy khi L biến thiên để (U_RC) _max thì ta có \(\left\{ \begin{array}{l}{Z_C} = \frac{{{Z_L} + \sqrt {Z_L^2 + 4{R^2}} }}{2}\\{\left( {{U_{RC}}} \right)_{\max }} = \frac{{U\left( {{Z_L} + \sqrt {Z_L^2 + 4{R^2}} } \right)}}{{2R}} = U\frac{{{Z_C}}}{R}\end{array} \right.\)