Từ vị trí A người ta quan sát một cây cao (hình vẽ).
Biết AH = 4m, HB = 20m,
Chiều cao của cây gần nhất với giá trị nào sau đây?
A. 17,5m
B. 17m
C. 16,5m
D. 16m
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Trong tam giác AHB, ta có
Suy ra
Suy ra
Áp dụng định lí sin trong tam giác ABC, ta được:
Phương pháp giải
Sử dụng các hệ thức lượng trong tam giác
1. Định lí côsin
Cho tam giác ABC có BC = a, AC = b và AB = c
Ta có
a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Hệ quả
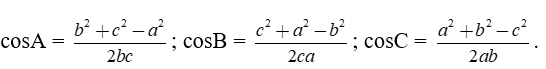
2. Định lí sin
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
Ta có
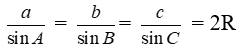
Xem thêm kiến thức liên quan
Lý thuyết Hệ thức lượng trong tam giác (Kết nối tri thức) hay, chi tiết | Toán lớp 10
20 câu Trắc nghiệm Hệ thức lượng trong tam giác (Kết nối tri thức) có đáp án – Toán lớp 10
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB = 24m, . Chiều cao h của tháp gần với giá trị nào sau đây?
Tam giác ABC có AB = c, BC = a, CA = b. Các cạnh a, b, c liên hệ với nhau bởi đẳng thức . Khi đó góc bằng bao nhiêu độ?
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt giác kế thẳng đứng cách chân tháp một khoảng CD = 60m, giả sử chiều cao của giác kế là OC = 1m. Quay thanh giác kế sao cho khi ngắm theo thanh OB ta nhìn thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc . Chiều cao của ngọn tháp gần với giá trị nào sau đây:
Tam giác ABC vuông tại A, có AB = c, AC = b. Gọi là độ dài đoạn phân giác trong góc . Tính theo b và c
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc . Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?
Tam giác ABC cân tại C, có AB = 9cm và . Gọi D là điểm đối xứng của B qua C. Tính độ dài cạnh AD
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
Cho tam giác ABC vuông tại A có AB = 5cm, BC = 13cm. Gọi góc và . Hãy chọn kết luận đúng khi so sánh và
Tam giác ABC có ba đường trung tuyến thỏa mãn . Khi đó tam giác này là tam giác gì?
Tam giác ABC có AB = c, BC = a, CA = b. Gọi là độ dài ba đường trung tuyến, G trọng tâm. Xét các khẳng định sau:
(I)
(II)
Trong các khẳng định đã cho có:
Tam giác ABC có AB = 3, AC = 6 và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC
Tam giác vuông cân tại A có AB = 2a. Đường trung tuyến BM có độ dài là: