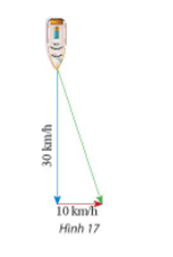
Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như Hình 17. Tính độ dài vectơ tổng của hai vectơ mói trên.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta đặt tên các điểm như hình vẽ sau:
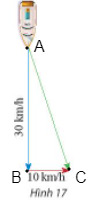
Khi đó vectơ vận tốc con tàu là với .
Vectơ vận tốc dòng nước là với .
Ta có vectơ tổng của hai vectơ trên là .
Do đó: .
Lại có AB và BC vuông góc nên tam giác ABC vuông tại B, áp dụng định lí Pythagore ta có: AC2 = AB2 + BC2 = 302 + 102 = 1000
Suy ra AC = km/h.
Vậy độ dài của vectơ tổng của hai vectơ đã cho là km/h.
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
a) ;
b) \.
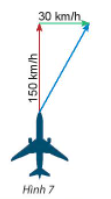
Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.
Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:
a) ;
b) ;
c) .
Cho hình thang ABCD có hai đáy là AB và DC. Cho biết . Chứng minh hai vectơ và cùng hướng.
Hai người cùng kéo một con thuyền với hai lực có độ lớn lần lượt là 400 N, 600 N (Hình 8). Cho biết góc giữa hai vectơ là 60°. Tìm độ lớn của vectơ hợp lực là tổng của hai lực và .
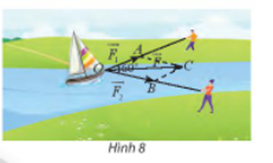
Cho ba lực và cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của đều là 10 N và . Tìm độ lớn của lực .
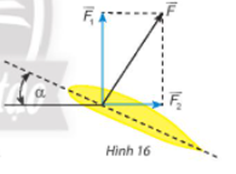
Khi máy bay nghiêng cánh một góc α, lực của không khí tác động vuông góc với cánh và bằng tổng của lực nâng và lực cản (Hình 16). Cho biết α = 30° và . Tính và theo a.
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ:
a) ;
b) ;
c) .
Cho tứ giác ABCD, thực hiện các phép cộng và trừ vectơ sau:
a) ;
b) ;
c) .
Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài của các vectơ sau:
a) ;
b) .
Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
a) ;
b) .
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng:
a) ;
b) .
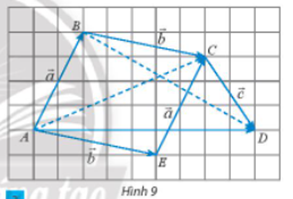
Cho ba vectơ được biểu diễn như Hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh các kết quả tìm được:
a) ;
.
b) ;
.