Một cái cổng hình bán nguyệt rộng 6,8 m, cao 3,4m. Mặt đường dưới cổng được chia thành hai làn cho xe ra vào.
a) Viết phương trình mô phỏng cái cổng.
 Giải bởi Vietjack
Giải bởi Vietjack
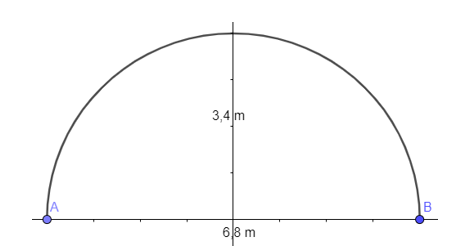
a) Giả sử cái cổng hình bán nguyệt có dạng như hình vẽ
Cái cổng là nửa hình tròn có bán kính R = 3,4 m
Phương trình mô phỏng cái cổng là phương trình đường tròn tâm O(0; 0) bán kính R = 3,4 m có dạng: x2 + y2 = 11,56.
c) (C) có tâm M(2; 3) và tiếp xúc với đường thẳng 3x – 4y + 9 = 0,
Lập phương trình đường tròn (C) trong các trường hợp sau:
a) (C) có tâm O(0; 0) và có bán kính R = 9;
c) Viết phương trình tiếp tuyến với (C) song song với đường thẳng 8x + 6y + 99 = 0.
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm toạ độ tâm và bán kính của đường tròn đó.
a) x2 + y2 + 2x + 2y – 9 = 0;
Cho đường tròn (C) có phương trình x2 + y2 – 6x – 2y – 15 = 0.
a) Chứng tỏ rằng điểm A(0; 5) thuộc đường tròn (C);
Lập phương trình đường tròn tiếp xúc với hai trục toạ độ Ox, Oy và đi qua điểm A(2; 1).
c) Viết phương trình tiếp tuyến với (C) song song với đường thẳng 8x + 6y + 99 = 0.
Cho đường tròn (C) có phương trình x2 + y2 – 6x – 2y – 15 = 0.
a) Chứng tỏ rằng điểm A(0; 5) thuộc đường tròn (C);