Chứng minh rằng với mọi tam giác ABC, ta có a = 2RsinA, b = 2RsinB, c = 2RsinC, trong đó R là bán kính đường tròn ngoại tiếp tam giác.

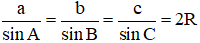
Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó

Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao ha, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác

Trong tam giác ABC. Chứng minh rằng

a) Góc A nhọn khi và chỉ khi a2 < b2 + c2

b) Góc A tù khi và chỉ khi a2 > b2 + c2

c) Góc A vuông khi và chỉ khi a2 = b2 + c2

Tại sao hai góc bù nhau lại có sin bằng nhau và cos đối nhau?

Từ hệ thức a2 = b2 + c2 - 2bc.cosA trong tam giác, hãy suy ra định lý Pi-ta-go.

Trong tập hợp các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.

Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?

Hãy nhắc lại định lí côsin trong tam giác. Từ các hệ thức này hãy tính cosA, cosB, cosC theo các cạnh của tam giác.

Nhắc lại định nghĩa tích vô hướng của hai vectơ a→ và b→. Tích vô hướng này với |a→| và |b→| không đổi đạt giá trị lớn nhất và nhỏ nhất khi nào?

Trong mặt phẳng Oxy cho vectơ a→(-3; 1) và b→(2; 2). Hãy tính tích vô hướng a→.b→.