Cho tam giác ABC và một điểm M tùy ý. Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Phương pháp giải
1. Tổng của hai vectơ
Định nghĩa. Cho hai vectơ 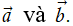
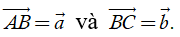
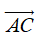
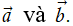
Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.
2. Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì
3. Tính chất của phép cộng các vectơ
Với ba vectơ 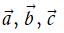
• 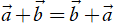
• 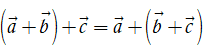
• 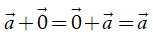
Xem thêm một số kiến thức liên quan:
20 câu Trắc nghiệm Tổng và hiệu của hai vectơ (Kết nối tri thức) có đáp án – Toán lớp 10
Lý thuyết Tổng và hiệu của hai vectơ (Kết nối tri thức) hay, chi tiết | Toán lớp 10
Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?
Cho hình thang ABCD có đáy là AB và CD. Gọi M và N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai?
Cho hình chữ nhật ABCD và số thực k> 0. Tập hợp các điểm M thỏa mãn đẳng thức
Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng?
Cho hai điểm A, B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức là
Cho tam giác đều ABC và điểm I thỏa mãn Mệnh đề nào sau đây đúng?
Cho tam giác ABC và điểm M thỏa mãn Khẳng định nào sau đây là đúng?
Cho đa giác lồi n cạnh. Có bao nhiêu vectơ khác mà giá của chúng tương ứng chứa các đường chéo của đa giác đã cho?
Cho tam giác ABC. Điểm M thỏa mãn điều kiện thì điều kiện cần và đủ là
Cho hai vectơ khác vectơ , không cùng phương và có độ dài bằng nhau. Khi đó giá của hai vectơ và thỏa mãn điều kiện nào sau đây?
Cho tam giác ABC với AB = c, BC = a, CA = b. Gọi CM là đường phân giác trong của góc C (M∈AB). Biểu thị nào sau đây là đúng?