Cho hình lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ-không, cùng phương với $\overrightarrow{OB}$, có điểm đầu và điểm cuối đều là các đỉnh của lục giác là:

Hướng dẫn giải

Đáp án đúng là: B

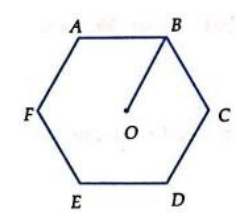
Các vectơ cùng phương với $\overrightarrow{OB}$ nếu chúng có giá song song hoặc trùng nhau.

Do đó các vectơ cùng phương với $\overrightarrow{OB}$ có điểm đầu và cuối là các đỉnh của lục giác là: $\overrightarrow{BE},\overrightarrow{EB},\overrightarrow{DC},\overrightarrow{CD},\overrightarrow{FA},\overrightarrow{AF}$.

Do đó có 6 vectơ thỏa mãn yêu cầu bài toán.

Hai vectơ cùng phương, cùng hướng

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Chú ý:

+ Trong hình trên, hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{PQ}$ cùng phương và có cùng hướng đi từ trái sang phải. Ta nói $\overrightarrow{MN}$ và $\overrightarrow{PQ}$ là hai vectơ cùng hướng.

+ Hai vectơ $\overrightarrow{EF}$ và $\overrightarrow{GH}$ cùng phương nhưng ngược hướng với nhau ($\overrightarrow{EF}$ có hướng từ trên xuống dưới và $\overrightarrow{GH}$ có hướng từ dưới lên trên). Ta nói hai vectơ $\overrightarrow{EF}$ và $\overrightarrow{GH}$ là hai vectơ ngược hướng.

Nhận xét:

+ Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

+ Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

Giải thích: Ta thấy nếu ba điểm A, B, C thẳng hàng thì hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ có giá trùng nhau nên chúng cùng phương. Ngược lại, nếu hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương thì ta suy ta hai đường thẳng AB và AC phải song song hoặc trùng nhau. Mà hai đường thẳng này có điểm A là điểm chung, do đó đường thẳng AB và AC trùng nhau. Khi đó ta có ba điểm A, B, C thẳng hàng. Vì vậy, ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

Bài tập liên quan: 

Cho tam giác ABC, có thể xác định được bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh A, B, C?

A. 2

B. 6

C. 9

D. 12

Cách giải:

Đáp án đúng là: B

Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau.

Vectơ khác vectơ-không là vectơ có điểm đầu khác điểm cuối.

Các vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh A, B, C là: $\overrightarrow{AB},\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{CB},\overrightarrow{CA},\overrightarrow{AC}$.

Do đó có 6 vectơ thỏa mãn yêu cầu bài toán.

Tham khảo thêm một số tài liệu liên quan:

Lý thuyết Khái niệm vectơ (Chân trời sáng tạo) | Toán lớp 10

Trắc nghiệm Khái niệm vectơ (Chân trời sáng tạo) – Toán lớp 10