Cho hình bình hành ABCD, điểm M thỏa mãn 4(vecto AM) = vecto AB + vecto AC...

Question

Cho hình bình hành ABCD, điểm M thỏa mãn 4AM→=AB→+AC→+AD→. Khi đó điểm M là

VietJack · Accepted Answer

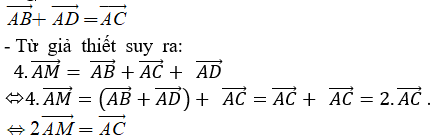
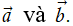
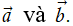
Đáp án A Do ABCD là hình bình hành nên: Suy ra: M nằm giữa A và C; AC = 2AM Do đó: M là trung điểm của AC. Lý thuyết 1. Tổng của hai vectơ: Định nghĩa. Cho hai vectơ Lấy một điểm A tùy ý, vẽ Vectơ được gọi là tổng của hai vectơ Ta kí hiệu tổng của hai vectơ Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ. 2. Quy tắc hình bình hành Nếu ABCD là hình bình hành thì 3. 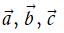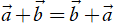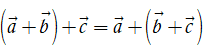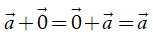Tính chất của phép cộng các vectơ Với ba vectơ tùy ý ta có • (tính chất giao hoán); • (tính chất kết hợp); • (tính chất của vectơ – không). 4. 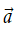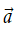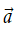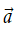Hiệu của hai vectơ a) Vectơ đối Cho vectơ Vectơ có cùng độ dài và ngược hướng với được gọi là vectơ đối của vectơ , kí hiệu là -. 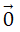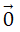Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của Đặc biệt, vectơ đối của vectơ là vectơ . b) Định nghĩa hiệu của hai vectơ Định nghĩa. 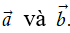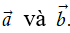Cho hai vectơ Ta gọi hiệu của hai vectơ là vectơ Như vậy Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có Chú ý: 1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ. 2) Với ba điểm tùy ý A, B, C ta luôn có (quy tắc ba điểm); (quy tắc trừ). 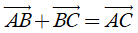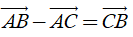Xem thêm một số kiến thức liên quan: 20 câu Trắc nghiệm Tổng và hiệu của hai vectơ (Kết nối tri thức) có đáp án – Toán lớp 10 Lý thuyết Tổng và hiệu của hai vectơ (Kết nối tri thức) hay, chi tiết | Toán lớp 10

Câu hỏi:

Cho hình bình hành ABCD, điểm M thỏa mãn $4 \vec{AM} = \vec{AB} + \vec{AC} + \vec{AD}$ . Khi đó điểm M là

A. trung điểm AC

B. điểm C

C. trung điểm AB

D. trung điểm AD

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Khẳng định nào sau đây đúng?

Câu 2:

Cho hai vectơ $\vec{a}, \vec{b}$ thỏa mãn $|\vec{a}| = 1$ , $|\vec{b}| = 1$ và hai vectơ $\vec{u} = \frac{2}{5} \vec{a} - 3 \vec{b}$ , $\vec{v} = \vec{a} + \vec{b}$ vuông góc với nhau. Xác định góc α giữa hai vectơ

Câu 3:

Cho Parabol (P): y = $\frac{x^{2}}{4}$ và đường thẳng y = 2x - 1. Khi đó:

Câu 4:

Cho A={0;1;2;3;4}; B={2;3;4;5;6}. Tập hợp A\B bằng:

Câu 5:

Cho 2 vectơ đơn vị $\vec{a} . \vec{b}$ thỏa mãn $|\vec{a} + \vec{b}| = 2$ . Hãy xác định $(3 \vec{a} - 4 \vec{b}) . (2 \vec{a} + 5 \vec{b})$

Câu 6:

Cho hàm số f(x) = $x^{2}$ - 6x + 1. Khi đó:

Câu 7:

Cho A(2;5); B(1;3) và C(5;-1). Tìm tọa độ điểm K sao cho $\vec{AK} = 3 \vec{BC} + 2 \vec{CK}$

Câu 8:

Trong mặt phẳng Oxy cho A(-1;1); B(1;3) và C(1; -1). Khẳng định nào sau đây đúng.

Câu 9:

Phương trình $x^{2}$ - mx + 1 = 0 có hai nghiệm âm phân biệt khi:

Câu 10:

Cho A = (– $\infty$ ;–2]; B = [3;+ $\infty$ ) và C = (0;4). Khi đó tập (A $\cup$ B) $\cap$ C là:

Câu 11:

Cho $\vec{OM} (- 2; - 1)$ , $\vec{ON} (3; - 1)$ . Tính góc của $(\vec{OM}, \vec{ON})$

Câu 12:

Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có M(1;-1), N(5;-3) và P thuộc trục Oy, trọng tâm G của tam giác nằm trên trục Ox.Toạ độ của điểm P là

Câu 13:

Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

Câu 14:

Tìm tất cả các giá trị thực của tham số m để phương trình ( $m^{2}$ -1)x = m-1 có nghiệm đúng với mọi x thuộc R.

Đề thi liên quan

Câu hỏi mới nhất