Tài liệu chuyên đề Chuyển động tròn đều Vật Lí lớp 10 gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Vật Lí 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Vật Lí 10 word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Chuyển động tròn đều

Tài liệu gồm 2 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Biến dạng của vật rắn :

Chuyên đề 2: BIẾN DẠNG CỦA VẬT RẮN

A. TÓM TẮT LÝ THUYẾT

1. Biến dạng đàn hồi, biến dạng kéo và biến dạng nén

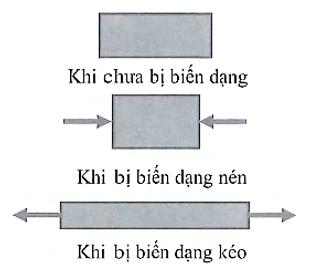
Ÿ   Khi không có ngoại lực tác dụng, vật tắn có kích thước và hình dạng xác định.

Ÿ   Khi có ngoại lực tác dụng, vật rắn thay đổi hình dạng và kích thước, ta nói vật rắn bị biến dạng.

     +) Biến dạng kéo: kích thước của vật theo phương tác dụng của lực tăng lên so với kích thước tự nhiên của nó.

     +) Biến dạng nén: kích thước của vật theo phương tác dụng của lực giảm đi so với kích thước tự nhiên của nó.

Ÿ   Khi ngừng tác dụng lực nếu vật rắn lấy lại được hình dạng và kích thước ban đầu thì biến dạng của vật là biến dạng đàn hồi.

2. Các đặc tính của lò xo

Ÿ   Các lò xo đều có tính đàn hồi. Khi chịu lực tác dụng, lò xo bị biến dạng đàn hồi.

Ÿ   Xét với lò xo thẳng, độ biến dạng đặc trưng cho sự biến dạng của lò xo, được xác định bằng hiệu số giữa chiều dài lò xo khi bị biến dạng và chiều dài tự nhiên của lò xo.

     +) Khi lò xo không biến dạng: độ biến dạng của lò xo bằng không.

     +) Khi lò xo biến dạng nén: độ biến dạng của lò xo âm, độ lớn của độ biến dạng được gọi là độ nén.

     +) Khi lò xo biến dạng kéo: độ biến dạng của lò xo dương và được gọi là độ dãn.

Ÿ   Tính đàn hồi của lò xo được đặc trung bới một hằng số là độ cứng \({\rm{k}}\), đơn vị trong hệ \({\rm{SI}}\) là \({\rm{N}}/{\rm{m}}\).

Ÿ   Giới hạn đàn hồi của lò xo là giới hạn trong đó vật rắn còn giữ được tính đàn hồi của nó.

3. Lực đàn hồi của lò xo - Định luật Hooke

B. BÀI TẬP KHỞI ĐỘNG

Câu 1. Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo

A. tỉ lệ nghịch với độ biến dạng của lò xo.               B. tỉ lệ thuận với độ biến dạng của lò xo.

C. tỉ lệ với khối lượng của vật.                                  D. tỉ lệ nghịch với khối lượng của vật.

Câu 2. Chọn phương án sai khi nói về hệ số đàn hồi?

A. Hệ số đàn hồi phụ thuộc vào bản chất của vật đàn hồi.

B. Nếu đơn vị của lực là \(\left( {\rm{N}} \right)\) và đơn vị chiều dài là (cm) thì hệ số đàn hồi có đơn vị là \(\left( {{\rm{N}}/{\rm{cm}}} \right)\).

C. Lò xo càng dài thì độ hệ số đàn hồi càng lớn.

D. Hệ số đàn hồi còn được gọi là độ cứng.

Câu 3: Điều nào sau đây là sai khi nói về đặc điểm của lực đàn hồi?

A. Lực đàn hồi xuất hiện khi vật có tính đàn hồi bị biến dạng.

B. Khi độ biến dạng của vật càng lớn thì lực đàn hồi cũng càng lớn, giá trị của lực đàn hồi là không có giới hạn.

C. Lực đàn hồi có độ lớn tỉ lệ với độ biến dạng của vật biến dạng.

D. Lực đàn hồi luôn ngược hướng với biến dạng.

Câu 4: Điều nào sau đây là sai khi nói về lực đàn hồi?

A. Với cùng độ biến dạng như nhau, độ lớn của lực đàn hồi phụ thuộc vào kích thước và bản chất của vật đàn hồi.

B. Với các mặt tiếp xúc bị biến dạng, lực đàn hồi vuông góc với các mặt tiếp xúc.

C. Với các vật như lò xo, dây cao su, thanh dài, lực đàn hồi hướng dọc theo trục của vật.

D. Lực đàn hồi có độ lớn tỉ lệ nghịch với độ biến dạng của vật biến dạng.

Câu 5: Điều nào sau đây là sai khi nói về đặc điểm của lực đàn hồi?

A. Lực đàn hồi xuất hiện khi vật có tính đàn hồi bị biến dạng.

B. Khi độ biến dạng của vật càng lớn thì lực đàn hồi cũng càng lớn, giá trị của lực đàn hồi là không có giới hạn.

C. Lực đàn hồi có độ lớn tỉ lệ với độ biến dạng của vật biến dạng.

D. Lực đàn hồi luôn ngược hướng với biến dạng.

Câu 6. Lực đàn hồi xuất hiện khi

     A. vật đứng yên.                                                         B. vật chuyển động có gia tốc.

     C. vật đặt gần mặt đất.                                               D. vật có tính đàn hồi bị biến dạng.

Câu 7. Vật nào dưới đây không có tính đàn hồi?

     A. Quả bóng bàn.                                                       B. Viên đất sét.

     C. Sợi dây cao su.                                                       D. Lò xo bút bi.

Câu 8. Hình ảnh nào sau đây mô tả biến dạng kéo?

     A. Hình (1).                      B. Hình (2).                      C. Hình (3).                      D. Hình (4).

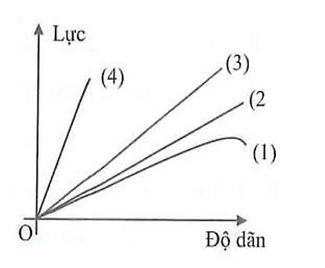
Câu 9. Đồ thị hình bên biểu diễn mối quan hệ giữa lực tác dụng vào đầu dưới của lò xo và độ dãn của nó tương ứng với bốn lò xo treo thẳng đứng (1), (2), (3) và (4). Lò xo không tuân theo định luật Hooke là

     A. (1).

     B. (2).

     C. (3).

     D. (4).

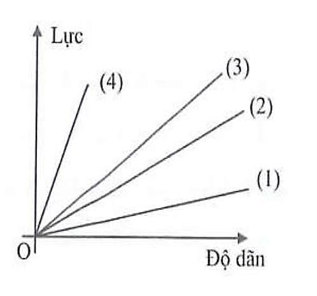
Câu 10. Đồ thị hình bên biểu diễn mối quan hệ giữa lực tác dụng vào đầu dưới của lò xo và độ dãn của nó tương ứng với bốn lò xo treo thẳng đứng (1), (2), (3) và (4). Lò xo có độ cứng lớn nhất là

A. (1).

B. (2).

C. (3).

D. (4).

BẢNG ĐÁP ÁN

C. CÁC DẠNG BÀI TẬP

Ví dụ 1 Tại cùng một nơi trên Trái Đất, hai con lắc lò xo treo thẳng đứng, lò xo thứ nhất bị dãn ra \({\rm{\Delta }}{\ell _1}\) khi treo vật có khối lượng \({m_1}\), lò xo thứ hai bị dãn ra \({\rm{\Delta }}{\ell _2} = \frac{{{\rm{\Delta }}{\ell _1}}}{2}\) khi treo vật có khối lượng \({m_2} = 2{m_1}\). Giả sử cả hai lò xo có khối lượng không đáng kể và có độ cứng lần lượt là \({{\rm{k}}_1}\) và \({{\rm{k}}_2}\). Hệ thức liên hệ giữa \({{\rm{k}}_1}\) và \({{\rm{k}}_2}\) là

     A. \({{\rm{k}}_2} = 4{{\rm{k}}_1}\).                               B. \({{\rm{k}}_1} = 4{{\rm{k}}_2}\).                        C. \({{\rm{k}}_1} = {{\rm{k}}_2}\).                                  D. \({{\rm{k}}_1} = 2{{\rm{k}}_2}\).

Phân tích:

Khi lò xo cân bằng ta có: ${\overrightarrow{\mathrm{F}}}_{\mathrm{dh}}+\overrightarrow{\mathrm{P}}=\overrightarrow{0}\to \{\begin{array}{cccccccccccccccccccc}{\overrightarrow{\mathrm{F}}}_{\mathrm{dh}}\uparrow \downarrow \overrightarrow{\mathrm{P}}\{{\mathrm{F}}_{\mathrm{dh}}=\mathrm{P}& & & & & & & & & & & & & & & & & & & \end{array}$

Áp dụng cho hai lò xo trong hai trường hợp \({{\rm{m}}_1}\) và \({{\rm{m}}_2}\) từ đó suy ra hệ thức cần tìm.

Lời giải: Chọn A.

Khi lò xo cân bằng ta có: \({{\rm{F}}_{{\rm{dh}}}} = {\rm{P}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\rm{k}}_2}.\left| {{\rm{\Delta }}{\ell _2}} \right| = {{\rm{m}}_2}{\rm{g}}}\\{{{\rm{k}}_1}.\left| {{\rm{\Delta }}{\ell _1}} \right| = {{\rm{m}}_1}{\rm{g}}}\end{array} \Rightarrow {{\rm{k}}_2} = \frac{{{{\rm{m}}_2}}}{{{\rm{\;}}{{\rm{m}}_1}}}.\left| {\frac{{{\rm{\Delta }}{\ell _1}}}{{{\rm{\Delta }}{\ell _2}}}} \right|{\rm{.}}{{\rm{k}}_1} = 4{{\rm{k}}_1}} \right.\).

Ví dụ 2 Một lò xo treo thẳng đứng, vật nặng có khối lượng \({\rm{m}} = 100{\rm{\;g}}\), khi vật cân bằng thì nó dãn ra \(5{\rm{\;cm}}\). Bỏ qua khối lượng của lò xo, cho \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Thay vật \({\rm{m}}\) bằng vật \({\rm{m'}}\) để lò xo dãn ra \(8{\rm{\;cm}}\) thì khối lượng vật \({\rm{m'}}\) phải có giá trị là

A. \(130{\rm{\;g}}\).            B. \(160{\rm{\;g}}\).            C. \(160{\rm{\;kg}}\).           D. \(130{\rm{\;kg}}\).

Lời giải: Chọn B.

Khi hệ cân bằng ta có: \[\left\{ {\begin{array}{*{20}{l}}{{\rm{k}}{\rm{.}}\left| {{\rm{\Delta }}{\ell _1}} \right| = {{\rm{m}}_1}{\rm{g}}}\\{{\rm{k}}{\rm{.}}\left| {{\rm{\Delta }}{\ell _2}} \right| = {{\rm{m}}_2}{\rm{g}}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{k}} = \frac{{{{\rm{m}}_1}{\rm{g}}}}{{\left| {{\rm{\Delta }}{\ell _1}} \right|}} = 20{\rm{\;N}}/{\rm{m}}}\\{{{\rm{m}}_2} = \frac{{{\rm{k}}\left| {{\rm{\Delta }}{\ell _2}} \right|}}{{\rm{g}}} = \frac{{20.0,08}}{{10}} = 0,16{\rm{\;kg}} = 160{\rm{\;g}}}\end{array}} \right.} \right.\]

Ví dụ 3 Một lò xo khối lượng không đáng kể, có chiều dài tự nhiên là  được treo thẳng đứng đầu trên cố định, đầu dưới treo vật có khối lượng ${\mathrm{m}}_1=120\mathrm{g}$, khi cân bằng lò xo dãn ra thêm 2 cm . Cho \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Chiều dài của lò xo khi treo thêm một vật có khối lượng \({{\rm{m}}_2} = 40{\rm{\;g}}\) là

A. \(46{\rm{\;cm}}\).           B. \(43{\rm{\;cm}}\).            C. \(8{\rm{\;cm}}\).              D. \(6{\rm{\;cm}}\).

Lời giải: Chọn B.

Treo lần lượt vật \({{\rm{m}}_1},\left( {{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}} \right)\) vào đầu dưới lò xo thì lò xo dãn \({\rm{\Delta }}{\ell _1},{\rm{\Delta }}{\ell _2} > 0\),

Khi hệ cân bằng ta có: \(\left\{ {\begin{array}{*{20}{l}}{{\rm{k}}\left| {{\rm{\Delta }}{\ell _1}} \right| = {{\rm{m}}_1}{\rm{g}}}\\{{\rm{k}}\left| {{\rm{\Delta }}{\ell _2}} \right| = \left( {{{\rm{m}}_1} + {{\rm{m}}_2}} \right){\rm{g}}}\end{array} \Rightarrow \left| {{\rm{\Delta }}{\ell _2}} \right| = \frac{{\left( {{{\rm{m}}_1} + {{\rm{m}}_2}} \right)}}{{{{\rm{m}}_1}}}.\left| {{\rm{\Delta }}{\ell _1}} \right| = \frac{{\left( {120 + 40} \right)}}{{120}}.2 = \frac{8}{3}{\rm{\;cm}}} \right.\).

Vậy chiều dài của lò xo khi treo vật $\mathrm{\ell }={\mathrm{\ell }}_0+|\mathrm{\Delta }{\mathrm{\ell }}_2|=40+\frac{8}{3}\approx 43\mathrm{cm}$

Ví dụ 4 Hình vẽ sau biểu diễn sự phụ thuộc của độ lớn lực đàn hồi \({\rm{F}}\left( {\rm{N}} \right)\) theo chiều dài \(\ell \left( {{\rm{cm}}} \right)\) của lò xo. Độ biến dạng của lò xo khi lực đàn hồi có độ lớn \(2{\rm{\;N}}\) là

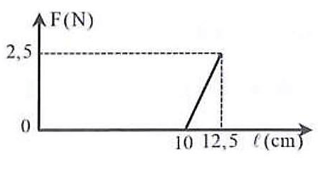
A. 2,5 cm.                         B. 10 cm.

C. 2 cm.                            D. 3 cm.

Phân tích:

Độ lớn lực đàn hồi: $\mathrm{F}=\mathrm{k}|\mathrm{\Delta }\mathrm{\ell }|=\mathrm{k}|\mathrm{\ell }-{\mathrm{\ell }}_0|$

Trên đồ thị ta chú ý 2 vị trí đặc biệt có thể lấy được các thông số cần thiết là: \(\left( {{{\rm{F}}_1} = 0;{\ell _1} = 10{\rm{\;cm}}} \right)\) và và \(\left( {{{\rm{F}}_2} = 2,5{\rm{\;N}};{\ell _2} = 12,5{\rm{\;cm}}} \right)\) từ đó giải tìm giá trị độ cứng \({\rm{k}}\).

Lời giải: Chọn C.

Khi \(\left\{ {\begin{array}{*{20}{l}}{{\ell _1} = 10{\rm{\;cm}}}\\{{\rm{\;}}{{\rm{F}}_1} = 0}\end{array} \Rightarrow {\ell _0} = {\ell _1} = 10{\rm{\;cm}}} \right.\).

Khi \(\left\{ {\begin{array}{*{20}{l}}{{\ell _2} = 12,5{\rm{\;cm}}}\\{{\rm{\;}}{{\rm{F}}_2} = 2,5{\rm{\;N}}}\end{array} \Rightarrow {\rm{k}} = \frac{{{{\rm{F}}_2}}}{{\left| {{\ell _2} - {\ell _0}} \right|}} = 100{\rm{\;N}}/{\rm{m}}} \right.\).

Khi \({{\rm{F}}_3} = 2{\rm{\;N}} \Rightarrow \left| {{\rm{\Delta }}\ell } \right| = \frac{{{{\rm{F}}_3}}}{{\rm{k}}} = \frac{2}{{100}} = 0,02{\rm{\;m}} = 2{\rm{\;cm}}\).