Tài liệu chuyên đề Động lượng Vật Lí lớp 10 gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Vật Lí 10. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Vật Lí 10 word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Động lượng

Tài liệu gồm 2 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Các loại va chạm: 

Chuyên đề 2: CÁC LOẠI VA CHẠM

A. TÓM TẮT LÝ THUYẾT

1. Phân loại va chạm

  Va chạm là một quá trình tương tác đặc biệt giữa hai vật, có những tính chất sau:

     - Thời gian tương tác rất ngắn (cỡ \({10^{ - 3}}{\rm{s}}\));

     - Lực tương tác có độ lớn đáng kể;

     - Ngay sau va chạm, vị trí của hai vật chưa kịp biến đổi nhưng vận tốc của hai vật biến đổi.

  Ta chỉ xét hai loại va chạm đơn giản sau:

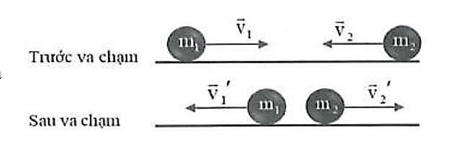
     +) Va chạm đàn hồi: là va chạm trong đó xuất

hiện biến dạng đàn hồi trong khoảng thời gian va chạm. Sau va chạm, vật lấy lại hình dạng ban đầu và

tiếp tục chuyển động tách rời nhau.

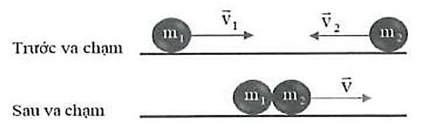
     +) Va chạm mềm (hay còn gọi là va chạm không đàn hồi): là va chạm mà sau khi xảy ra hai vật dính

vào nhau và chuyển động với cùng vận tốc.

2. Động lượng và năng lượng trong va chạm

Ÿ   Trong các va chạm, động lượng và tổng năng lượng được bảo toàn.

Ÿ   Trong va chạm đàn hồi, động năng của hệ sau va chạm bằng động năng của hệ trước va chạm.

Ÿ   Trong va chạm mềm, động năng của hệ sau va chạm nhỏ hơn động năng của hệ trước va chạm.

Phần động năng giảm đi sau va chạm của hệ đã chuyển hóa thành nội năng (tỏa nhiệt).

B. BÀI TẬP KHỞI ĐỘNG

Câu 1. Hiện tượng nào sau đây là va chạm mềm?

A. Quả bóng đang bay đập vào tường và nảy ra.

B. Viên đạn đang bay xuyên vào và nằm gọn trong bao cát.

C. Viên đạn xuyên qua một tấm bia trên đường bay của nó.

D. Quả bóng tennis đập xuống sân thi đấu.

Câu 2. Hiện tượng nào sau đây là va chạm đàn hồi?

A. Sự va chạm của mặt vợt cầu lông vào quả cầu lông .

B. Bắn một đầu đạn vào một bị cát.

C. Bắn một viên bi-a vào một viên bi-a khác.

D. Ném một cục đất sét vào tường.

Câu 3. Đại lượng vật lí nào sau đây sẽ bảo toàn trong va chạm đàn hồi và không bảo toàn trong va chạm mềm?

     A. Động lượng.                B. Động năng.                  C. Vận tốc.                        D. Gia tốc.

Câu 4. Phát biểu nào sau đây là đúng về va chạm?

A. Va chạm đàn hồi chỉ được bảo toàn động năng, không bảo toàn động lượng.

B. Mọi loại va chạm đều bảo toàn tổng động lượng.

C. Va chạm mềm bảo toàn cả động lượng và động năng.

D. Va chạm đàn hồi chỉ bảo toàn động lượng, không bảo toàn động năng.

Câu 5. Quả cầu A khối lượng \({{\rm{m}}_1}\) chuyển động với vận tốc \({{\rm{\vec v}}_1}\) va chạm vào quả cầu \({\rm{B}}\) khối lượng \({{\rm{m}}_2}\) đứng yên. Sau va chạm, cả hai quả cầu có cùng vận tốc \({{\rm{\vec v}}_2}\). Bỏ qua mọi ma sát và lực cản. Hệ thức nào sau đây là đúng?

     A. ${\mathrm{m}}_1{\overrightarrow{\mathrm{v}}}_1=({\mathrm{m}}_1+{\mathrm{m}}_2){\overrightarrow{\mathrm{v}}}_2$                                                                          B. ${\mathrm{m}}_1{\overrightarrow{\mathrm{v}}}_1=-{\mathrm{m}}_2{\overrightarrow{\mathrm{v}}}_2$

     C. ${\mathrm{m}}_1{\overrightarrow{\mathrm{v}}}_1={\mathrm{m}}_2{\overrightarrow{\mathrm{v}}}_2$                        D. ${\mathrm{m}}_1{\overrightarrow{\mathrm{v}}}_1=\frac{1}{2}({\mathrm{m}}_1+{\mathrm{m}}_2){\overrightarrow{\mathrm{v}}}_2$

Câu 6. Quả cầu \({\rm{A}}\) khối lượng \({{\rm{m}}_1}\) chuyển động với vận tốc \({{\rm{\vec v}}_1}\) tới va chạm với quả cầu B khối lượng \({{\rm{m}}_2}\) chuyển động với vận tốc \({{\rm{\vec v}}_2}\) như hình vẽ. Sau va chạm, cả hai quả cầu có cùng vận tốc \({\rm{\vec v}}\) như hình vẽ. Bỏ qua mọi ma sát và lực cản. Hệ thức nào sau đây là đúng?

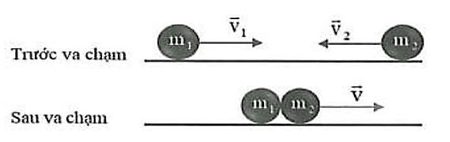
     A. \({{\rm{m}}_1}{{\rm{\vec v}}_1} - {{\rm{m}}_2}{{\rm{\vec v}}_2} = \left( {{{\rm{m}}_1} + {{\rm{m}}_2}} \right){\rm{\vec v}}\).                               B. \({{\rm{m}}_1}{{\rm{\vec v}}_1} + {{\rm{m}}_2}{{\rm{\vec v}}_2} = \left( {{{\rm{m}}_1} + {{\rm{m}}_2}} \right){\rm{\vec v}}\).

     C. \({{\rm{m}}_1}{{\rm{\vec v}}_1} - {{\rm{m}}_2}{{\rm{\vec v}}_2} = \frac{1}{2}\left( {{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}} \right){\rm{\vec v}}\).                D. \({{\rm{m}}_1}{{\rm{\vec v}}_1} + {{\rm{m}}_2}{{\rm{\vec v}}_2} = \frac{1}{2}\left( {{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}} \right){\rm{\vec v}}\).

Câu 7. Hai quả cầu \({\rm{A}}\) và \({\rm{B}}\) chuyển động ngược chiều trên một đường thẳng, tới va chạm đàn hồi xuyên tâm. Sau va chạm, hai quả cầu chuyển động theo hướng ngược lại như hình vẽ. Bỏ qua mọi ma sát và lực cản. Hệ thức nào sau đây là đúng?

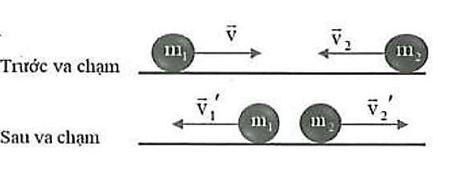
     A. \({{\rm{m}}_1}{{\rm{\vec v}}_1} - {{\rm{m}}_2}{{\rm{\vec v}}_2} = {{\rm{m}}_1}{\rm{\vec v}}_1^{\rm{'}} - {{\rm{m}}_2}{\rm{\vec v}}_2^{\rm{'}}\).              B. \({{\rm{m}}_1}{{\rm{\vec v}}_1} - {{\rm{m}}_2}{{\rm{\vec v}}_2} = \frac{1}{2}\left( {{\rm{\;}}{{\rm{m}}_1}{\rm{\vec v}}_1^{\rm{'}} + {{\rm{m}}_2}{\rm{\vec v}}_2^{\rm{'}}} \right)\).

     C. \({{\rm{m}}_1}{{\rm{\vec v}}_1} + {{\rm{m}}_2}{{\rm{\vec v}}_2} = {{\rm{m}}_1}{\rm{\vec v}}_1^{\rm{'}} + {{\rm{m}}_2}{\rm{\vec v}}_2^{\rm{'}}\).             D. \({{\rm{m}}_1}{{\rm{\vec v}}_1} + {{\rm{m}}_2}{{\rm{\vec v}}_2} = \frac{1}{2}\left( {{\rm{\;}}{{\rm{m}}_1}{\rm{\vec v}}_1^{\rm{'}} + {{\rm{m}}_2}{\rm{\vec v}}_2^{\rm{'}}} \right)\).

Câu 8. Hai quả cầu khối lượng \({{\rm{m}}_1}\) và \({{\rm{m}}_2}\) đang chuyển động thẳng đều với các vận tốc \({{\rm{\vec v}}_1}\) và \({{\rm{\vec v}}_2}\) cùng phương thì va chạm với nhau. Bỏ qua mọi ma sát và lực cản. Nếu va chạm của hai quả cầu là và chạm mềm thì vận tốc sau va chạm của hệ hai quả cầu có biểu thức là

     A. \({\rm{\vec v}} = \frac{{{{\rm{m}}_1}{{{\rm{\vec v}}}_1} + {{\rm{m}}_2}{{{\rm{\vec v}}}_2}}}{{{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}}}\).                                                       B. \({\rm{\vec v}} = \frac{{{{\rm{m}}_1}{{{\rm{\vec v}}}_1} - {{\rm{m}}_2}{{{\rm{\vec v}}}_2}}}{{{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}}}\).

     C. \({\rm{\vec v}} = \frac{{{{\rm{m}}_1}{{{\rm{\vec v}}}_1} - {{\rm{m}}_2}{{{\rm{\vec v}}}_2}}}{{{\rm{\;}}{{\rm{m}}_1} - {{\rm{m}}_2}}}\).                                                        D. \({\rm{\vec v}} = \frac{{{{\rm{m}}_1}{{{\rm{\vec v}}}_1} + {{\rm{m}}_2}{{{\rm{\vec v}}}_2}}}{{2\left( {{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}} \right)}}\).

Câu 9. Bắn một viên đạn khối lượng \({\rm{m}}\) vào một mẩu gỗ có khối lượng \({\rm{M}}\) đặt trên mặt nằm ngang nhẵn. Đạn mắc vào gỗ và cùng chuyển động với vận tốc \({\rm{V}}\). Bỏ qua mọi ma sát và lực cản của môi trường. Biểu thức xác định vận tốc của đạn lúc bắn là

     A. \(v = \frac{{\left( {m + M} \right)V}}{m}\).                                                            B. \(v = \frac{{MV}}{{m + M}}\).

     C. \(v = \frac{{MV}}{{2\left( {m + M} \right)}}\).                                                        D. \(v = \frac{{\left( {m + M} \right)V}}{{2m}}\).

Câu 10. Trên mặt phẳng nằm ngang, một hòn bi sắt có khối lượng \({{\rm{m}}_1}\) chuyển động sang phải với tốc độ là \({{\rm{v}}_1}\) tới va chạm đàn hồi với một hòn bi thủy tinh có khối lượng \({{\rm{m}}_2}\) đang chuyển động sang trái với tốc độ là \({{\rm{v}}_2}\). Sau va chạm, hòn bi sắt đứng yên. Bỏ qua mọi ma sát và lực cản. Vận tốc của hòn bi thủy tinh sau va chạm là

     A. \({\rm{v}}_2^{\rm{'}} = \frac{{{{\rm{m}}_1}{{\rm{v}}_1} + {{\rm{m}}_2}{{\rm{v}}_2}}}{{{\rm{\;}}{{\rm{m}}_2}}}\).                                                    B. \({\rm{v}}_2^{\rm{'}} = \frac{{{{\rm{m}}_1}{{\rm{v}}_1} - {{\rm{m}}_2}{{\rm{v}}_2}}}{{{\rm{\;}}{{\rm{m}}_2}}}\).

     C. \(v_2^{\rm{'}} = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}\).                   D. \({\rm{v}}_2^{\rm{'}} = \frac{{{{\rm{m}}_1}{{\rm{v}}_1} - {{\rm{m}}_2}{{\rm{v}}_2}}}{{{\rm{\;}}{{\rm{m}}_1} + {{\rm{m}}_2}}}\).

BẢNG ĐÁP ÁN

C. CÁC DẠNG BÀI TẬP

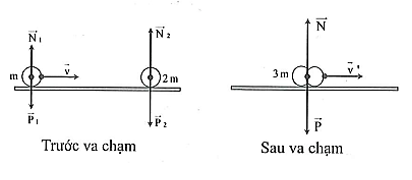
Ví dụ 1 Một vật khối lượng \({\rm{m}}\) đang chuyển động theo phương ngang với vận tốc \({\rm{v}}\) thì va chạm vào vật khối lượng \(2{\rm{\;m}}\) đang đứng yên. Sau va chạm, hai vật dính vào nhau và chuyển động với cùng vận tốc. Bỏ qua ma sát, vận tốc của hệ sau va chạm là

     A. \(\frac{{\rm{v}}}{3}\).      B. v.                                   C. \(3{\rm{v}}\).                   D. \(\frac{{\rm{v}}}{2}\).

Lời giải: Chọn A.

     Xét hệ hai vật gồm m và \(2{\rm{\;m}}\).

     Ngoại lực tác dụng lên hệ gồm trọng lực \({{\rm{\vec P}}_1};{{\rm{\vec P}}_2}\) và phản lực \({{\rm{\vec N}}_1};{{\rm{\vec N}}_2}\) như hình vẽ.

     Do tổng ngoại lực tác dụng lên hệ triệt tiêu nên hệ là kín.

     Động lượng của hệ trước va chạm là:

     \({\rm{p}} = {\rm{m}}{\rm{.v}} + 2{\rm{\;m}}.0 = {\rm{m}}{\rm{.v}}\).

     Động lượng của hệ sau va chạm là: \({\rm{p'}} = \left( {{\rm{m}} + 2{\rm{\;m}}} \right){\rm{.v'}} = 3{\rm{m}}{\rm{.v'}}\).

     Áp dụng định luật bảo toàn động lượng ta có: \(p = p' \Leftrightarrow m.v = 3m.v' \Rightarrow v' = \frac{v}{3}\).

     Vậy, sau va chạm hai vật dính vào nhau và chuyển động theo hướng cũ với cùng vận tốc

Ví dụ 2 Một vật có khối lượng 25 kg rơi nghiêng một góc \({60^ \circ }\) so với đường nằm ngang với tốc độ \(36{\rm{\;km}}/{\rm{h}}\) vào một xe goòng chứa cát đứng yên trên đường ray nằm ngang (như hình vẽ). Cho khối lượng xe là \(975{\rm{\;kg}}\), bỏ qua mọi ma sát và lực cản của môi trường. Tốc độ của xe goòng sau khi vật cắm vào là

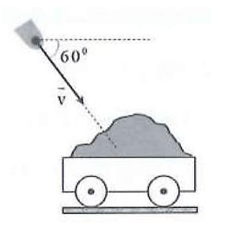
     A. \(0,125{\rm{\;m/s}}\).     B. \(0,45{\rm{\;m/s}}\).

     C. \(0,217{\rm{\;m/s}}\).     D. \(0,78{\rm{\;m/s}}\).

Phân tích:

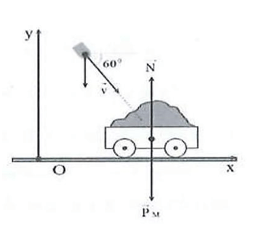
     Hệ vật gồm vật \({\rm{m}} = 25{\rm{\;kg}}\) và xe \({\rm{M}} = 975{\rm{\;kg}}\).

     Các ngoại lực tác dụng lên hệ vật: trọng lực \({{\rm{\vec P}}_{\rm{M}}}\) của xe và \({{\rm{\vec P}}_{\rm{m}}}\) của vật, phản lực \({\rm{\vec N}}\) của mặt đường tác dụng lên xe.

     Xét theo phương ngang, tổng ngoại lực tác dụng lên hệ triệt tiêu nên có thể coi là hệ kín và áp dụng định luật bảo toàn động lượng theo phương này.

Lời giải: Chọn A.

Hệ vật gồm vật \({\rm{m}} = 25{\rm{\;kg}}\) và xe \({\rm{M}} = 975{\rm{\;kg}}\), trước va chạm \({{\rm{v}}_{\rm{m}}} = 36{\rm{\;km/h}} = 10{\rm{\;m/s}};{{\rm{v}}_{\rm{M}}} = 0\).

Sau khi vật cắm vào xe, hệ vật và xe cùng chuyển động với tốc độ V.

Xét theo phương \({\rm{Ox}}\) nằm ngang, chiều dương là chiều chuyển động của vật trước khi rơi vào xe, ta có:

Động lượng của hệ lúc đầu: \({\rm{p}} = {\rm{M}}{\rm{.}}{{\rm{v}}_{\rm{M}}} + {\rm{m}}{\rm{.}}{{\rm{v}}_{\rm{m}}}{\rm{.cos}}{60^ \circ } = 25.10.{\rm{cos}}{60^ \circ } = 125{\rm{\;kg}}{\rm{.m/s}}\).

Động lượng của hệ ngay sau khi vật rơi vào xe:

\({\rm{p'}} = \left( {{\rm{M}} + {\rm{m}}} \right){\rm{.V}} = \left( {975 + 25} \right){\rm{.V}} = 1000{\rm{\;V}}\).

Theo phương ngang hệ được coi là kín, áp dụng định luật bảo toàn động lượng ta có:

\({\rm{p}} = {\rm{p'}} \Rightarrow 1000{\rm{\;V}} = 125 \Rightarrow {\rm{V}} = 0,125{\rm{\;m}}/{\rm{s}}{\rm{.\;}}\)

Ví dụ 3 Viên đạn khối lượng \({\rm{m}} = 100{\rm{\;g}}\) đang bay với vận tốc \({\vec v_0}\) theo phương ngang đến cắm vào bao cát khối lượng \({\rm{M}} = 400{\rm{\;g}}\) treo ở đầu sợi dây dài \(\ell  = 1{\rm{\;m}}\) đang đứng yên ở vị trí cân bằng, đầu kia của sợi dây treo vào điểm cố định. Bỏ qua lực cản của không khí, lấy \({\rm{g}} = 10{\rm{\;m/}}{{\rm{s}}^2}\). Sau khi cắm vào bao cát hệ chuyển động lên đến vị trí dây treo lệch với phương thẳng đứng một góc lớn nhất bằng \({60^ \circ }\). Giá trị của \({{\rm{v}}_0}\) bằng

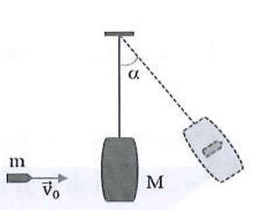
     A. \(10{\rm{\;m/s}}\).          B. \(5\sqrt {10} {\rm{\;m/s}}\).

     C. \(10\sqrt 5 {\rm{\;m/s}}\).                                          D. \(50{\rm{\;m/s}}\).

Phân tích:

     Va chạm giữa viên đạn và bao cát là va chạm mềm, do đó động lượng của hệ viên đạn và bao cát là bảo toàn. Áp dụng định luật bảo toàn động lượng ta sẽ xác định được vận tốc của hệ ngay sau va chạm. Khi bỏ qua lực cản của không khí, cơ năng của hệ là bảo toàn, áp dụng định luật bảo toàn cơ năng để xác định mối liên hệ giữa \({{\rm{v}}_0}\) và các thông số mà đề bài đã cho.

Lời giải: Chọn B.

     Xét hệ gồm viên đạn và bao cát, va chạm giữa viên đạn và bao cát là va chạm mềm, thời điểm xảy ra va chạm hệ là kín.

     Động lượng của hệ ngay trước khi xảy ra va chạm là: \({\rm{p}} = {\rm{m}}{{\rm{v}}_0}\).

     Động lượng của hệ ngay sau khi xảy ra va chạm là: \({\rm{p'}} = \left( {{\rm{m}} + {\rm{M}}} \right)\).V.

     Áp dụng định luật bảo toàn động lượng của hệ, ta có:

      \({\rm{m}}{{\rm{v}}_0} = \left( {{\rm{m}} + {\rm{M}}} \right){\rm{V}} \Rightarrow {\rm{V}} = \frac{{\rm{m}}}{{{\rm{m}} + {\rm{M}}}}{{\rm{v}}_0} = \frac{{{{\rm{v}}_0}}}{5}\)

     Chọn mốc tính thế năng tại vị trí cân bằng của bao cát \({\rm{M}}\).

     Cơ năng của hệ ngay sau khi xảy ra va chạm là:

      \({\rm{W}} = \frac{1}{2}\left( {{\rm{\;m}} + {\rm{M}}} \right){{\rm{V}}^2} = \frac{1}{2}\left( {0,1 + 0,4} \right){\left( {\frac{{{{\rm{v}}_0}}}{5}} \right)^2} = \frac{{{\rm{v}}_0^2}}{{100}}\)

     Cơ năng của hệ khi dây treo lệch với phương thẳng đứng góc \(\alpha \) lớn nhất là:

      \({\rm{W'}} = \left( {{\rm{m}} + {\rm{M}}} \right){\rm{.g}}{\rm{.h}} = \left( {{\rm{m}} + {\rm{M}}} \right){\rm{.g}}{\rm{.}}\ell \left( {1 - {\rm{cos}}\alpha } \right) = \left( {0,1 + 0,4} \right).10.1.\left( {1 - {\rm{cos}}{{60}^ \circ }} \right) = 2,5{\rm{\;J}}\)

     Áp dụng định luật bảo toàn cơ năng, ta có: \({\rm{W}} = {\rm{W'}} \Leftrightarrow \frac{{{\rm{v}}_0^2}}{{100}} = 2,5 \Rightarrow {{\rm{v}}_0} = 5\sqrt {10} {\rm{\;m}}/{\rm{s}}\).

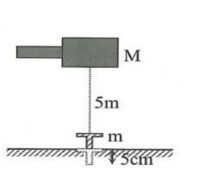
Ví dụ 4 Một búa máy khối lượng M = 400 kg thả rơi tự do từ độ cao \(5{\rm{\;m}}\) so với mặt đất xuống đất đóng vào cọc có khối lượng \({\rm{m}} = 100{\rm{\;kg}}\) trên mặt đất làm cọc lún sâu vào trong đất \(5{\rm{\;cm}}\). Coi va chạm giữa búa và cọc là va chạm mềm, chiều cao của cọc không đáng kể, lấy \({\rm{g}} = 9,8{\rm{\;m}}/{{\rm{s}}^2}\), lực cản của đất coi như không đổi có độ lớn là

     A. \(318500{\rm{\;N}}\).     B. \(628450{\rm{\;N}}\).     

     C. \(154360{\rm{\;N}}\).      D. \(250450{\rm{\;N}}\).

Phân tích:

     Va chạm giữa búa máy và cọc là va chạm mềm, do đó động lượng của hệ búa máy và cọc là bảo toàn. Áp dụng định luật bảo toàn động lượng ta sẽ xác định được vận tốc của hệ ngay sau va chạm. Để xác định lực cản của đất, ta cần áp dụng định lí biến thiên cơ năng.

Lời giải: Chọn A.

Tốc độ của búa máy ngay trước khi xảy ra va chạm là: $\mathrm{V}=\sqrt{2\mathrm{g}\mathrm{h}}=\sqrt{2.9,8.5}=7\sqrt{2}\mathrm{m}/\mathrm{s}$

Động lượng của hệ búa máy và cọc trước khi va chạm là:

\({\rm{p}} = {\rm{M}}{\rm{.V}} = 400.7\sqrt 2  = 2800\sqrt 2 {\rm{\;kg}}{\rm{.m/s}}{\rm{.\;}}\)

Động lượng của hệ búa máy và cọc ngay sau khi va chạm là: \({\rm{p'}} = \left( {{\rm{M}} + {\rm{m}}} \right){\rm{.V'}} = 500{\rm{\;}}{{\rm{V}}^{\rm{'}}}\).

Áp dụng định luật bảo toàn động lượng, ta có:

\({\rm{p'}} = {\rm{p}} \Rightarrow {\rm{p'}} = 500{\rm{\;}}{{\rm{V}}^{\rm{'}}} = 2800\sqrt 2  \Rightarrow {\rm{V'}} = 5,6\sqrt 2 {\rm{\;m}}/{\rm{s}}{\rm{.\;}}\)

Chọn mốc tính thế năng tại mặt đất.

Cơ năng của hệ vật ngay sau khi va chạm:

\({\rm{W}} = {{\rm{W}}_{\rm{d}}} = \frac{1}{2}\left( {{\rm{m}} + {\rm{M}}} \right){\left( {{\rm{V'}}} \right)^2} = \frac{1}{2}.500{(5,6\sqrt 2 )^2} = 15680{\rm{\;J}}.\)

     Cơ năng của hệ khi cọc lún sâu vào đất một đoạn \(5{\rm{\;cm}}\) là:

      \({\rm{W'}} = {{\rm{W}}_{\rm{t}}} = {\rm{mgh}} = 100.9,8.\left( { - 0,05} \right) =  - 49{\rm{\;J}}{\rm{.\;}}\)

     Áp dụng định lí biến thiên cơ năng, ta có:

      \({\rm{W'}} - {\rm{W}} = {{\rm{F}}_{\rm{C}}}{\rm{.s}} \Leftrightarrow  - 49 - 15680 = {{\rm{F}}_{\rm{C}}}.0,05 \Rightarrow {{\rm{F}}_{\rm{C}}} =  - 314580{\rm{\;N}}{\rm{.\;}}\)