Chuyên đề Động học | Vật lí lớp 10

Van Anh Ngày: 12-03-2024 Lớp 10

Mua tài liệu 196

Tài liệu chuyên đề Động học Vật Lí lớp 10 gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Vật Lí 10.

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Vật Lí 10 word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Động học

Tài liệu gồm 4 Chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Gia tốc. Chuyển động thẳng biến đổi :

Chuyên đề 2: GIA TỐC. CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU.

A. TÓM TẮT LÝ THUYẾT

1. Gia tốc

· Gia tốc là đại lượng vectơ, đặc trưng cho độ biến thiên của vận tốc theo thời gian.

· Gia tốc trung bình được xác định theo biểu thức: ${{\rm{\vec a}}_{\rm{t}}} = \frac{{{\rm{\Delta \vec v}}}}{{{\rm{\Delta t}}}} = \frac{{{{{\rm{\vec v}}}_2} - {{{\rm{\vec v}}}_1}}}{{{\rm{\Delta t}}}}$.

· Khi ${\rm{\Delta t}}$ rất nhỏ, gia tốc trung bình trở thành gia tốc tức thời.

· Trong chuyển động thẳng, gia tốc trung bình được xác định theo biểu thức:

${{\rm{a}}_{tb}} = \frac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}} = \frac{{{{\rm{v}}_2} - {{\rm{v}}_1}}}{{{\rm{\Delta t}}}}$

· Đơn vị của gia tốc trong hệ SI là ${\rm{m/}}{{\rm{s}}^2}$.

2. Phân loại chuyển động thẳng

Dựa vào giá trị của gia tốc có thể phân chuyển động thẳng thành 3 loại:

· Nếu ${\rm{a}} = 0$ : chuyển động thẳng đều, vật có độ lớn vận tốc không đổi.

· Nếu ${\rm{a}} \ne 0$ và bằng hằng số: chuyển động thẳng biến đổi đều, vật có độ lớn vận tốc thay đổi (tăng hoặc giảm) đều theo thời gian.

+) Chuyển động thẳng nhanh dần đều: Vận tốc tăng đều theo thời gian, $\vec a$ và $\vec v$ cùng chiều.

+) Chuyển động thẳng chậm dần đều: Vận tốc giảm đều theo thời gian, $\vec a$ và $\vec v$ ngược chiều.

· Nếu ${\rm{a}} \ne 0$ nhưng không bằng hằng số: chuyển động thẳng phức tạp (không xét trong chương trình Vật lí phổ thông).

3. Các phương trình của chuyển động thẳng biến đổi đều

Công thức vận tốc: ${\rm{v}} = {{\rm{v}}_0} + {\rm{at}}$

Công thức độ dịch chuyển: ${\rm{d}} = \frac{{{{\rm{v}}_0} + {\rm{v}}}}{2}{\rm{.t}}$

Công thức tính quãng đường đi được:${\rm{s}} = {{\rm{v}}_0}{\rm{t}} + \frac{1}{2}{\rm{at}}{\;^2}$

Phương trình chuyển động: ${\rm{x}} = {{\rm{x}}_0} + {\rm{s}} = {{\rm{x}}_0} + {{\rm{v}}_0}{\rm{t}} + \frac{1}{2}{\rm{at}}{\;^2}$

+ Gốc thời gian được chọn sao cho ${{\rm{t}}_0} = 0$.

+ Chuyển động nhanh dần: $a.{v_0} > 0$.

+ Chuyển động chậm dần: $a.{v_0} < 0$.

$ \to {\rm{v}}\left( {\rm{t}} \right)$ là hàm số bậc nhất của thời gian.

$ \to {\rm{x}}\left( {\rm{t}} \right)$ và ${\rm{s}}\left( {\rm{t}} \right)$ là hàm số bậc 2 của thời gian.

Công thức liên hệ giữa gia tốc, vận tốc và quãng đường đi: ${{\rm{v}}^2} - {\rm{v}}_0^2 = 2{\rm{as}}$

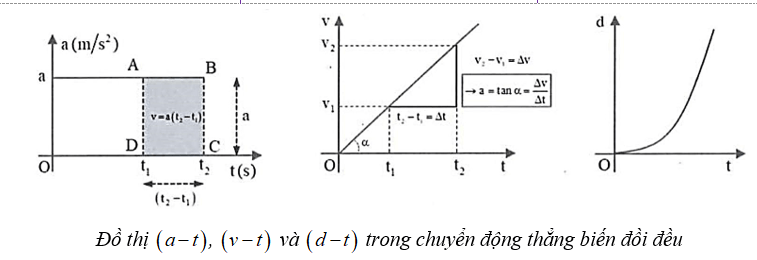
4. Đồ thị của chuyển động thẳng biến đổi đều

Đồ thị gia tốc - thời gian ${\rm{a}}\left( {\rm{t}} \right)$ là đường thẳng song song với trục thời gian.

Đồ thị vận tốc - thời gian ${\rm{v}}\left( {\rm{t}} \right)$ là đường thẳng xiên góc, tạo với trục thời gian một góc $\alpha $.

Đồ thị tọa độ - thời gian ${\rm{x}}\left( {\rm{t}} \right)$ là một phần đường parabol.

B. BÀl TẬP KHỞI ĐỘNG

Câu 1. Hình vẽ nào sau đây biểu diễn đúng mối liên hệ giữa các vectơ gia tốc ${\rm{\vec a}}$, vận tốc ban đầu ${\vec v_0}$ và vận tốc tức thời ${\rm{\vec v}}$ trong chuyển động thẳng nhanh dần đều?

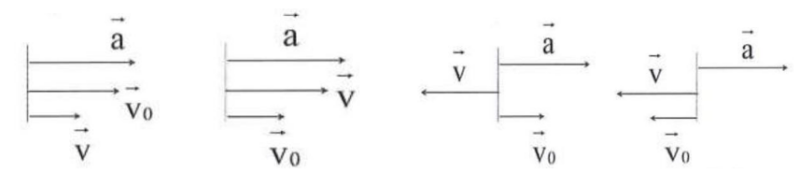
(I) (II) (III) (IV)

A. Hình (I). B. Hình (II). C. Hình (III). D. Hình (IV).

Câu 2. Hình vẽ nào sau đây biểu diễn đúng mối liên hệ giữa các vectơ gia tốc ${\rm{\vec a}}$, vận tốc ban đầu ${\vec v_0}$ và vận tốc tức thời $\vec v$ trong chuyển động thẳng chậm dần đều?

(I) (II) (III) (IV)

A. Hình (I). B. Hình (II). C. Hình (III). D. Hình (IV).

Câu 3. Gia tốc là một đại lượng

A. đại số, đặc trưng cho sự biến thiên nhanh hay chậm của chuyển động.

B. đại số, đặc trưng cho tính không đổi của vận tốc.

C. vectơ, đặc trưng cho sự biến thiên nhanh hay chậm của chuyển động.

D. vectơ, đặc trưng cho sự biến thiên nhanh hay chậm của vận tốc.

Câu 4. Chuyển động thẳng biến đổi đều là chuyển động có

A. quỹ đạo là đường thẳng, vectơ gia tốc và vận tốc không đổi trong suốt quá trình chuyển động.

B. quỹ đạo là đường thẳng, vectơ gia tốc bằng không.

C. quỹ đạo là đường thẳng, vectơ gia tốc không đổi trong suốt quá trình chuyển động.

D. quỹ đạo là đường thẳng, vectơ vận tốc không đổi trong suốt quá trình chuyển động.

Câu 5. Vectơ gia tốc của chuyển động thẳng biến đổi đều

A. có phương vuông góc với vectơ vận tốc.

B. có độ lớn không đổi.

C. cùng hướng với vectơ vận tốc.

D. ngược hướng với vectơ vận tốc.

Câu 6. Chọn phương án sai.

Chuyển động thẳng nhanh dần đều có

A. vectơ gia tốc ngược chiều với vectơ vận tốc.

B. vận tốc tức thời là hàm số bậc nhất của thời gian.

C. tọa độ là hàm số bậc hai của thời gian.

D. gia tốc có độ lớn không đổi theo thời gian.

Câu 7. Đơn vị nào sau đây là đơn vị của gia tốc?

A. ${\rm{m}}/{{\rm{s}}^2}$. B. ${\rm{m}}/{\rm{s}}$. C. ${\rm{km}}/{\rm{h}}$. D. ${\rm{m}}{\rm{.}}{{\rm{s}}^2}$.

Câu 8. Công thức nào sau đây là công thức liên hệ giữa vận tốc, gia tốc và đường đi của chuyển động

thẳng biến đổi đều?

A. $v - {v_0} = \sqrt {2as} $. B. $v + {v_0} = \sqrt {2as} $. C. ${v^2} - v_0^2 = 2as$. D. ${v^2} + v_0^2 = 2as$.

Câu 9. Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là

A. $s = {v_0}t + \frac{{a{t^2}}}{2}\left( {a.{v_0} > 0} \right)$. B. $s = {v_0}t + \frac{{a{t^2}}}{2}\left( {a.{v_0} < 0} \right)$.

C. $s = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\left( {a.{v_0} > 0} \right)$. D. ${\rm{s}} = {{\rm{x}}_0} + {{\rm{v}}_0}{\rm{t}} + \frac{{{\rm{a}}{{\rm{t}}^2}}}{2}\left( {{\rm{a}}{\rm{.}}{{\rm{v}}_0} < 0} \right)$

Câu 10. Phương trình tọa độ của chuyển động thẳng chậm dần đều là

A. $x = {v_0}t + \frac{{a{t^2}}}{2}\left( {a.{v_0} > 0} \right)$. B. $x = {v_0}{t^2} + \frac{{a{t^2}}}{2}\left( {a.{v_0} < 0} \right)$.

C. $x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\left( {a.{v_0} > 0} \right)$. D. $x = {x_0} + {v_0}t + \frac{{a{t^2}}}{2}\left( {a.{v_0} < 0} \right)$.

BẢNG ĐÁP ÁN

01. B

02. D

03. D

04. C

05. B

06. A

07. A

08. C

09. A

10. D

C. CÁC DẠNG BÀI TẬP

DẠNG 1

VẬN DỤNG CÁC CÔNG THỨC CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU

Phương pháp giải

· Chọn một chiều dương và xác định dấu của vận tốc (cùng chiều dương: ${\rm{v}} > 0$, ngược chiều dương: $v < 0$ ).

· Dựa vào đặc điểm chuyển động của vật (nhanh dần đều, chậm dần đều), xác định dấu của gia tốc theo dấu của vận tốc (nhanh dần đều: $a.v > 0$, chậm dần đều: $a.v < 0$ ).

· Để đơn giản bài toán nên chọn gốc thời gian sao cho ${{\rm{t}}_0} = 0$, căn cứ vào yêu cầu cụ thể của bài toán để lựa chọn công thức phù hợp:

$\left\{ {\begin{array}{*{20}{l}}{{\rm{v}} = {{\rm{v}}_0} + {\rm{at}}}\\{{\rm{s}} = {{\rm{v}}_0}{\rm{t}} + \frac{1}{2}{\rm{at}}{\;^2}}\\{{{\rm{v}}^2} - {\rm{v}}_0^2 = 2{\rm{as}}}\end{array}} \right.$

Ví dụ 1 Một chiếc xe hơi giảm tốc chuyển động chậm dần đều từ $54{\rm{\;km/h}}$ còn $36{\rm{\;km/h}}$ trên quãng đường thẳng dài $125{\rm{\;m}}$. Chọn chiều dương là chiều chuyển động. Gia tốc của xe trên đoạn đường này là

A. $ - 1,48{\rm{\;m}}/{{\rm{s}}^2}$. B. $ - 0,72{\rm{\;m}}/{{\rm{s}}^2}$. C. $ - 0,5{\rm{\;m}}/{{\rm{s}}^2}$. D. $ - 1{\rm{\;m}}/{{\rm{s}}^2}$.

Phân tích:

Trong dữ kiện của bài toán đã cho sẵn chiều dương là chiều của chuyển động do đó vận tốc của xe có giá trị dương. Chuyển động là chậm dần đều nên tích a.v <0, vậy gia tốc phải có giá trị âm.

Từ các dữ kiện đã biết của bài toán là ${{\rm{v}}_0},{\rm{v}}$ và s ta có thể có hai hướng giải như sau:

$ \to $ Lập hệ phương trình

$ \to $ Sử dụng công thức mối liên hệ giữa vận tốc, gia tốc và quãng đường đi: ${{\rm{v}}^2} - {\rm{v}}_0^2 = 2{\rm{as}}$.

Trong quá trình làm bài, tùy vào khả năng biến đổi toán học để lựa chọn cách tính toán phù hợp, tuy nhiên nên chọn những công thức sao cho việc biến đổi là đơn giản và ngắn gọn nhất.

Lời giải: Chọn C.

Đổi đơn vị: ${{\rm{v}}_0} = 54{\rm{\;km/h}} = 15{\rm{\;m/s}};{\rm{v}} = 36{\rm{\;km/h}} = 10{\rm{\;m/s}}$.

Cách 1: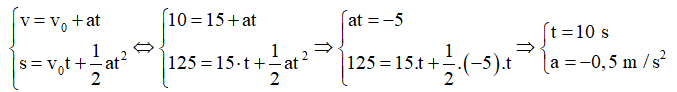

Cách 2: $v^{2} - v_{0}^{2} = 2 as \Leftrightarrow 10^{2} - 15^{2} = 2 . a .125 \Rightarrow a = - 0, 5 m / s^{2}$

Ví dụ 2 Khi ô tô đang chạy với vận tốc $10{\rm{\;m}}/{\rm{s}}$ trên đoạn đường thẳng thì người lái xe tăng ga và ô tô chuyển động nhanh dần. Sau $20{\rm{\;s}}$, ô tô đạt vận tốc $14{\rm{\;m/s}}$. Gia tốc a và vận tốc v của ô tô sau $40{\rm{\;s}}$ kể từ lúc bắt đầu tăng ga là

A. ${\rm{a}} = 0,7{\rm{\;m/}}{{\rm{s}}^2};{\rm{v}} = 38{\rm{\;m/s}}$. B. ${\rm{a}} = 0,2{\rm{\;m/}}{{\rm{s}}^2};{\rm{v}} = 18{\rm{\;m/s}}$.

C. $a = 0,2{\rm{\;m/}}{{\rm{s}}^2};{\rm{v}} = 8{\rm{\;m/s}}$. D. ${\rm{a}} = 1,4{\rm{\;m/}}{{\rm{s}}^2};{\rm{v}} = 66{\rm{\;m/s}}$.

Phân tích:

Sử dụng công thức vận tốc ${\rm{v}} = {{\rm{v}}_0} + at$ để xác định giá trị của gia tốc, từ đó tính được vận tốc của ô tô ở các thời điểm khác.

Lời giải: Chọn B.

Ta có ${{\rm{v}}_0} = 10{\rm{\;m/s}};{\rm{v}} = 14{\rm{\;m/s}}$.

Gia tốc của ô tô là: ${\rm{a}} = \frac{{{\rm{v}} - {{\rm{v}}_0}}}{{\rm{t}}} = \frac{{14 - 10}}{{20}} = 0,2{\rm{\;m}}/{{\rm{s}}^2}$.

Vận tốc của ô tô sau $40{\rm{\;s}}$ kể từ lúc bắt đầu tăng ga là: ${{\rm{v}}_{40}} = {{\rm{v}}_0} + {\left. {{\rm{at}}} \right|_{{\rm{t}} = 40{\rm{s}}}} = 10 + 0,2.40 = 18{\rm{\;m/s}}$.