Cho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến , phép quay Q(B, 60°), phép vị tự V(A, 3), ∆ABC biến thành ∆A1B1C1. Tìm diện tích ∆A1B1C1.
 Giải bởi Vietjack
Giải bởi Vietjack
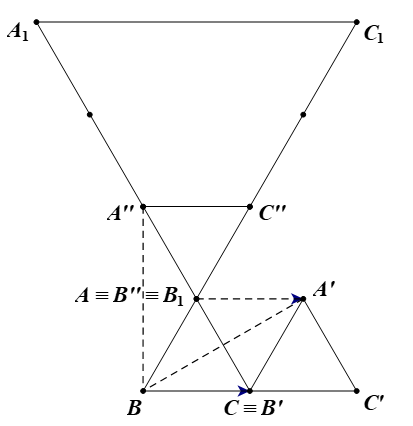
Ta có ∆ABC đều có cạnh bằng 2. Suy ra AB = AC = 2 và .
Vì phép tịnh tiến và phép quay đều là phép dời hình nên ảnh của ∆ABC qua phép tịnh tiến và phép quay Q(B, 60°) đều có các kích thước bằng các kích thước tương ứng của ∆ABC.
Gọi f là phép biến hình có được bằng thực hiện hai phép biến hình liên tiếp là phép tịnh tiến và phép quay Q(B, 60°).
Suy ra f là phép dời hình.
Do đó phép đồng dạng tỉ số 3 có được bằng cách thực hiện liên tiếp phép dời hình f và phép vị tự V(A, 3) biến ∆ABC thành ∆A1B1C1.
Vì vậy phép đồng dạng tỉ số 3 biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Khi đó A1B1 = 3AB = 3.2 = 6 và A1C1 = 3AC = 3.2 = 6.
Vì ∆ABC và ∆A1B1C1 đồng dạng với nhau nên .
Ta có .
Vậy diện tích ∆A1B1C1 bằng .
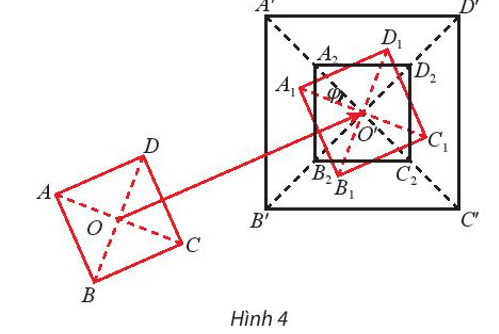
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi A1B1C1D1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A1, O’A’). Tìm ảnh A2B2C2D2 của hình vuông A1B1C1D1 qua phép quay Q(O’, φ).
b) Cho biết . Tìm ảnh của hình vuông A2B2C2D2 qua phép vị tự V(O’, k).
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.
Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hình thang JLKI và hình thang IHDC đồng dạng với nhau.
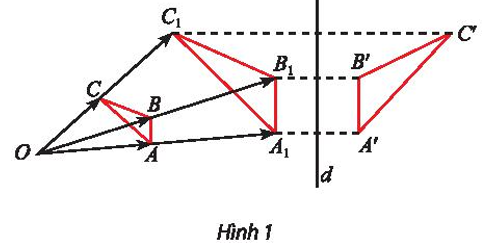
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Trong hình bên dưới, tìm các cặp hình có hình dạng giống nhau. Loại phép biến hình nào có thể biến hình này thành hình kia trong mỗi cặp?

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O bán kính R = 9 và cho điểm A khác O. Gọi (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ và phép vị tự . Tìm diện tích hình tròn (C’).
Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: . Hãy chứng minh g là một phép đồng dạng.