Tailieumoi.vn xin giới thiệu chuyên đề Hàm số lượng giác và phương trình lượng giác thuộc chương trình Toán 11. Chuyên đề gồm 165 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Chuyên đề Hàm số lượng giác và phương trình lượng giác
Phần 1: Phương pháp Tìm tập xác định, tập giá trị của hàm số lượng giác
1. Lý thuyết
a. Hàm số y = sinx
- Tập xác định: D = R
- Tập giá trị: [-1;1]
b. Hàm số y = cosx
- Tập xác định: D = R
- Tập giá trị: [-1;1]
c. Hàm số y = tanx
- Tập xác định: D = R \ {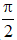 
+ kπ, k ∈ Z}
- Tập giá trị:R
d. Hàm số y = cotx
- Tập xác định: D = R \ { kπ, k ∈ Z}
- Tập giá trị: R
2. Các dạng bài tập
Dạng 1. Tìm tập xác định của hàm số lượng giác
- Phương pháp giải:
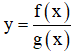xác định khi g(x) ≠ 0
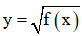xác định khi f(x) ≥ 0
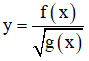xác định khi g(x) > 0
y = tan[u(x)] xác định khi u(x) ≠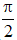 
+ kπ, k ∈ Z
y = cot[u(x)] xác định khi u(x) ≠ kπ, k ∈ Z
sin x ≠ 0 khi x ≠ kπ (k ∈ Z)
cos x ≠ 0 khi x ≠ 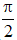+ kπ (k ∈ Z)
- Ví dụ minh họa:
Ví dụ 1. Tìm tập xác định của hàm số sau
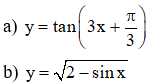
Lời giải
a)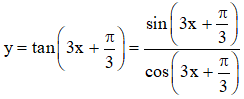 
Điều kiện xác định: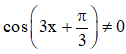 
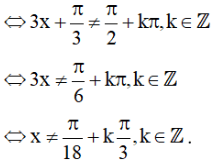
Vậy tập xác định của hàm số là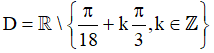 
b) Điều kiện xác định: 2 - sin x ≥ 0
⇔ sin x ≤ 2 (đúng ∀x ∈ R ) vì -1 ≤ sin x ≤ 1 ∀x ∈ R
Vậy tập xác định của hàm số là D = R.
Ví dụ 2. Tìm tập xác định của hàm số sau
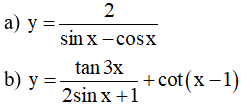
Lời giải
a) Điều kiện xác định: sin x - cos x ≠ 0 ⇔ sin x ≠ cos x (*)
+ Trường hợp 1: cosx = 0. Ta có sin2x + cos2x = 1 ⇔ sin2 x = 1 ⇔ sin x = ±1.
Hiển nhiên sin x ≠ cos x
+ Trường hợp 2: cos x ≠ 0. Chia cả hai vế cho cosx
Vậy tập xác định của hàm số là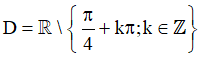 
b) Vì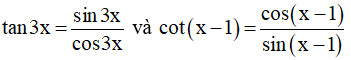 
Điều kiện xác định: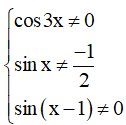 
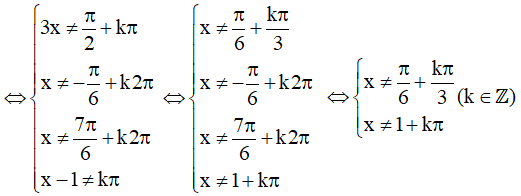
Vậy tập xác định của hàm số là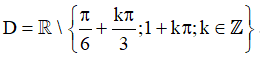 
Dạng 2. Tìm tập giá trị của hàm số lượng giác
- Phương pháp giải:
Sử dụng tính bị chặn của hàm số lượng giác
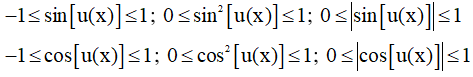
- Ví dụ minh họa:
Ví dụ 1. Tìm tập giá trị của các hàm số sau:
a) y = 2sin3x – 5
b) y = 2sin2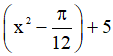
c) y = |cos(3x-2)| + 4
Lời giải
a) Ta có:
-1 ≤ sin 3x ≤ 1 ∀x ∈ R
⇔ -2 ≤ 2sin 3x ≤ 2 ∀x ∈ R
⇔ -7 ≤ 2sin 3x - 5 ≤ -3 ∀x ∈ R
Vậy tập giá trị: T = [-7;-3].
b) Ta có: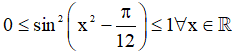 
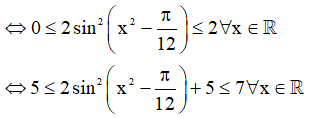
Vậy tập giá trị: T = [5;7].
c) Ta có: 0 ≤ |cos(3x - 2)| ≤ 1∀x ∈ R
⇔ 4 ≤ |cos(3x - 2)| + 4 ≤ 5∀x ∈ R
Vậy tập giá trị: T = [4;5].
Ví dụ 2. Tìm tập giác trị của các hàm số sau:
a)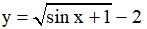 
b) y = cos2x + 4sinx +1
Lời giải
a) Điều kiện xác định: sinx +1 ≥ 0 ⇔ sinx ≥ -1∀x ∈ R.
Tập xác định D = R.
Ta có: -1 ≤ sin x ≤ 1 ∀x ∈ R
⇔ 0 ≤ sinx + 1 ≤ 2 ∀x ∈ R
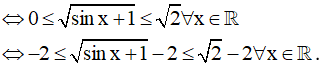
Vậy tập giá trị: T = [-2,√2 - 2 ]
b) y = cos2x + 4sinx +1 = 1 - 2sin2x + 4sinx +1 = -2sin2x + 4sinx + 2 = -2(sinx – 1)2 + 4.
Ta có: -1 ≤ sin x ≤ 1 ∀x ∈ R
⇔ -2 ≤ sin x - 1 ≤ 0 ∀x ∈ R
⇔ 0 ≤ (sin x - 1)2 ≤ 4 ∀x ∈ R
⇔ -8 ≤ -2(sin x - 1)2 ≤ 0 ∀x ∈ R
⇔ -4 ≤ -2(sin x - 1)2 + 4 ≤ 4 ∀x ∈ R .
Vậy tập giá trị: T = [-4;4].
Dạng 3. Tìm m để hàm số lượng giác có tập xác định là R
- Phương pháp giải:
m ≥ f(x) ∀x ∈ [a,b] => m ≥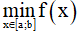 
m > f(x) ∀x ∈ [a,b] => m >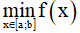 
m ≤ f(x) ∀x ∈ [a,b] => m ≤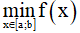 
m < f(x) ∀x ∈ [a,b] => m <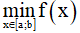 
- Ví dụ minh họa:
Ví dụ 1. Tìm m để hàm số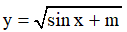 
xác định trên R.
Lời giải
Để hàm số xác định trên R thì sin x + m ≥ 0 ∀x ∈ R ⇔ -sin x∀x ∈ R .
Mà ta có -1 ≤ sin x ≤ 1 ∀x ∈ R ⇔ -1 ≤ -sin x ≤ 1 ∀x ∈ R
Nên m ≥ 1
Ví dụ 2. Tìm m để hàm số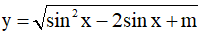 
xác định trên R.
Lời giải
Ta có: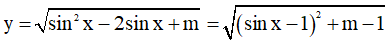 
Hàm số xác định trên R khi (sinx – 1)2 + m - 1 ≥ 0 ∀x ∈ R ⇔ m ≥ 1 - (sinx – 1)2 ∀x ∈ R
Ta có:
-1 ≤ sin x ≤ 1 ∀x ∈ R
⇔ -2 ≤ sin x - 1 ≤ 0 ∀x ∈ R
⇔ 0 ≤ (sinx – 1)2 ≤ 4 ∀x ∈ R
⇔ -4 ≤ -(sinx – 1)2 ≤ 0 ∀x ∈ R
⇔ -3 ≤ 1 - (sinx – 1)2 ≤ 1 ∀x ∈ R
Vậy m ≥ 1
3. Bài tập tự luyện
Câu 1. Tập xác định của hàm số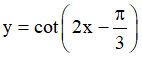 
là
Câu 2. Tập xác định của hàm số y = tan x + cot x là
Câu 3. Tập xác định của hàm số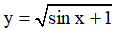 
là:
A. D = [ -1,+∞) B. D = R
C. D = R \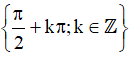 
D. D = (-∞, -1]
Câu 4. Tập xác định của hàm số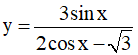 
là:
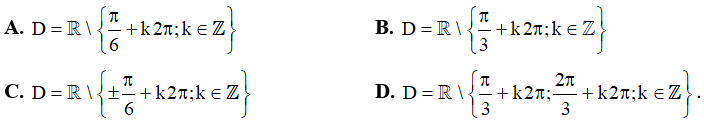
Câu 5. Tập xác định của hàm số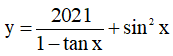 
là
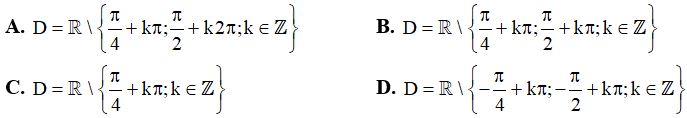
Câu 6. Tập xác định của hàm số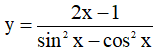 
là
Câu 7. Tập xác định của hàm số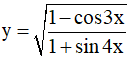 
là
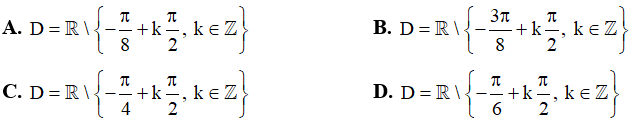
Câu 8. Hàm số nào dưới đây có tập xác định là R?
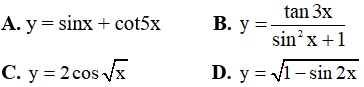
Câu 9. Tập giá trị của hàm số y = 1 – 2|sin2x| là
A. [1;3] B. [-1;1] C. [-1;3] D. [-1;0]
Câu 10. Tập giá trị của hàm số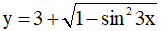 
là
A. [2;3] B. [1;2] C. [2;4] D. [3;4]
Câu 11. Tập giá trị của hàm số y = 2 + sinxcosx có dạng T = [m,M]. Giá trị của m là:
Câu 12. Tập giá trị của hàm số y = 2sin3x +1 là
A. [-1;1] B. [-5;7] C. [0;2] D. [-1;3]
Câu 13. Tìm m để hàm số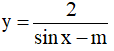 
xác định trên R.
A. m ∈ (-∞; -1) ∪ (1, +∞) B. m ∈ (-∞; -1] ∪ [1, +∞)
C. m ≠ 1 D. m ∈ [-1;1]
Câu 14. Hàm số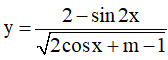 
có tập xác định R khi và chỉ khi:
A. m > 3 B. m < -1 C. m ≥ 3 D. m ≤ -1
Câu 15. Tìm tất cả các giá trị của tham số m để hàm số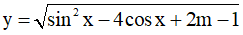 
có tập xác định là R.
A.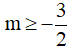 
B.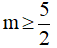 
C. Không có m thỏa mãn D. m ≥ 5
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
A |
D |
B |
C |
B |
C |
A |
D |
B |
D |
B |
D |
A |
A |
B |
Phần 2: Phương pháp Xét tính chẵn, lẻ, chu kì tuần hoàn của hàm số lượng giác
1. Lý thuyết
a) Tính chẵn, lẻ của hàm số:
* Định nghĩa:
- Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu: ∀x ∈ D thì -x ∈ D và f(-x) = f(x).
Đồ thị hàm số chẵn nhận trục tung Oy làm trục đối xứng.
- Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu: ∀x ∈ D thì -x ∈ D và f(-x) = - f(x).
Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.
* Đối với hàm số lượng giác:
- Hàm số y = sinx là hàm số lẻ trên D = R.
- Hàm số y = cosx là hàm số chẵn trên D = R.
- Hàm số y = tanx là hàm số lẻ trên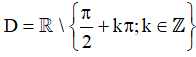 
- Hàm số y = cotx là hàm số lẻ trên D = R\ .
b) Tính tuần hoàn và chu kì của hàm số:
* Định nghĩa:
- Hàm số y = f(x) xác định trên tập hợp D, được gọi là hàm số tuần hoàn nếu có số T ≠ 0 sao cho với mọi x ∈ D ta có (x + T) ∈ D; (x - T) ∈ D và f(x + T) = f(x).
- Nếu có số dương T nhỏ nhất thỏa mãn các điều kiện trên thì T gọi là chu kì của hàm tuần hoàn f.
* Đối với hàm số lượng giác:
Hàm số y = sinx; y = cosx tuần hoàn với chu kì 2π.
Hàm số y = tanx; y = cotx tuần hoàn với chu kì π.
2. Các dạng bài tập
Dạng 1. Xét tính chẵn, lẻ của hàm số lượng giác
Phương pháp giải:
Bước 1: Tìm tập xác định D của hàm số, khi đó:
- Nếu D là tập đối xứng (tức là ∀x ∈ D => -x ∈ D ), ta thực hiện tiếp bước 2.
- Nếu D không phải là tập đối xứng (tức là ∃x ∈ D mà -x ∉ D ), ta kết luận hàm số không chẵn cũng không lẻ.
Bước 2: Xác định f(-x), khi đó:
- Nếu f(-x) = f(x) kết luận hàm số là hàm chẵn.
- Nếu f(-x) = - f(x) kết luận hàm số là hàm lẻ.
- Ngoài ra kết luận hàm số không chẵn cũng không lẻ.
Ví dụ minh họa:
Ví dụ 1: Xét tính chẵn, lẻ của các hàm số:
a) y = f(x) = sinx + tan2x
b) y = f(x) = cos3x + sin22x
c) y = f(x) = cosx + tan2x
Lời giải
a) Tập xác định: D = R là một tập đối xứng. Do đó ∀x ∈ D thì -x ∈ D
Ta có: f(-x) = sin(-x) + tan(-2x) = - sinx – tan2x = - (sinx + tan2x) = -f(x).
Vậy y = sinx + tan2x là hàm số lẻ.
b) Tập xác định: D = R là một tập đối xứng. Do đó ∀x ∈ D thì -x ∈ D .
Ta có: f(-x) = cos(-3x) + sin2(-2x) = cos3x + (-sin2x)2 = cos3x + sin22x = f(x).
Vậy y = cos3x + sin22x là hàm số chẵn.
c) Điều kiện xác định: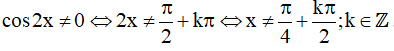 
Tập xác định: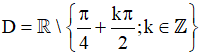 
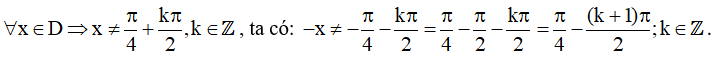
Đặt m = -(k + 1), k ∈ Z khi đó: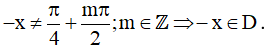 
.
Ta có: f(-x) = cos(-x) + tan(-2x) = cosx – tan2x
Nhận thấy: f(-x) ≠ f(x) và f(-x) ≠ -f(x)
Vậy f(x) = cosx + tan2x không phải là hàm số chẵn, không phải là hàm số lẻ.
Ví dụ 2: Xét tính chẵn, lẻ của các hàm số:
a) y = f(x) = |x|sinx
b) y = f(x) = cos(2x+1)
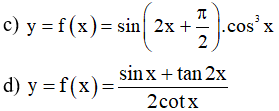
Lời giải
a) Tập xác định: D = R là một tập đối xứng. Do đó ∀x ∈ D thì -x ∈ D.
Ta có: f(-x) = |-x|sin(-x) = x.(-sinx) = -x.sinx = -f(x)
Vậy y = |x|sinx là hàm số lẻ.
b) Tập xác định: D = R là một tập đối xứng. Do đó ∀x ∈ D thì -x ∈ D
Ta có: f(-x) = cos[2(-x)+1] = cos(-2x+1) = cos(2x-1)
Nhận thấy f(-x) ≠ f(x) và f(-x) ≠ -f(x)
Vậy hàm số y = cos(2x-1) không phải hàm số chẵn, không phải hàm số lẻ.
c) Tập xác định: D = R là một tập đối xứng. Do đó ∀x ∈ D thì -x ∈ D
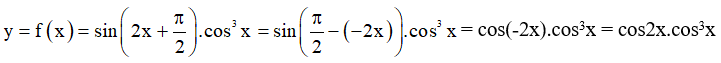
Ta có: f(-x) = cos(-2x) cos3(-x) = cos2xcos3x = f(x)
Vậy hàm số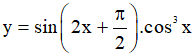 
là hàm số chẵn.
d) Điều kiện xác định: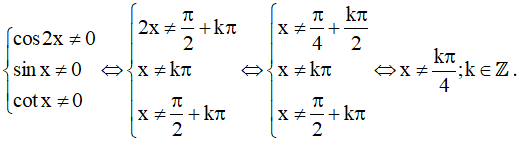 
.
Tập xác định: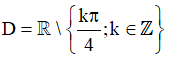 
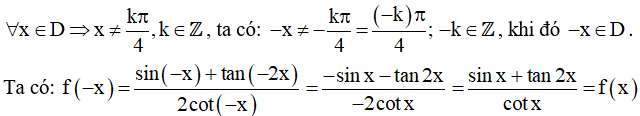
Vậy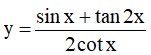 
là hàm số chẵn.
Dạng 2: Xét tính tuần hoàn, tìm chu kỳ của hàm số lượng giác
Phương pháp giải:
- Xét tính tuần hoàn và chu kì bằng định nghĩa.
- Sử dụng các kết quả sau:
+ Hàm số y = sin(ax + b) là một hàm số tuần hoàn với chu kì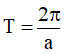 
.
+ Hàm số y = cos(ax + b) là một hàm số tuần hoàn với chu kì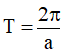 
.
+ Hàm số y = tan(ax + b) là một hàm số tuần hoàn với chu kì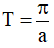 
+ Hàm số y = cot(ax + b) là một hàm số tuần hoàn với chu kì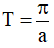 
+ Nếu hàm số y = f(x) tuần hoàn với chu kì T thì hàm số y = Af(x) (với A khác 0) tuần hoàn với chu kì T.
+ Nếu hàm số y = f(x) tuần hoàn với chu kì T thì hàm số y = f(x) + c (c là hằng số) tuần hoàn với chu kì T.
+ Nếu hàm số y = f1(x); y = f2(x);… y = fn(x) tuần hoàn với chu kì lần lượt là T1; T2; … Tn thì hàm số tuần hoàn với chu kì T là bội chung nhỏ nhất của T1; T2; … Tn.
Ví dụ minh họa:
Ví dụ 1: Tìm chu kì (nếu có) của các hàm số:
a) y = sin2x +1
b) y = -3tan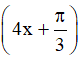
c) y = cos2x -1
d) y = sin2(2x - 3) + 5
Lời giải
a) Hàm số y = sin2x tuần hoàn với chu kì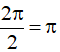 
Vậy hàm số y = sin2x +1 tuần hoàn với chu kì π.
b) Hàm số y = -3tan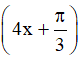 tuần hoàn theo chu kì 
.
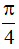c) Ta có: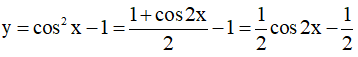 
Hàm số y = cos2x tuần hoàn với chu kì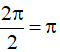 
.
Vậy hàm số y = cos2x - 1 tuần hoàn với chu kì π.
d) Ta có: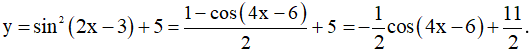 
Hàm số y = cos(4x+6) tuần hoàn với chu kì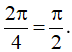 
Vậy hàm số y = sin2(2x-3) + 5 tuần hoàn với chu kì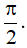 
Ví dụ 2: Tìm chu kì (nếu có) của các hàm số:
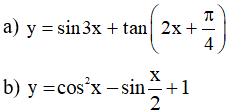
c) y = sin4x.cos2x
d) y = sinx + cos(√2x)
Lời giải
a) Hàm số y = sin3x tuần hoàn với chu kì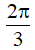 
Hàm số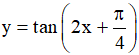 
tuần hoàn với chu kì 
.
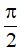Vậy hàm số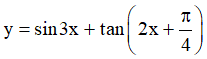 
tuần hoàn với chu kì T là bội chung nhỏ nhất của 
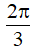và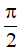 
, do đó T = 2π.
b) Hàm số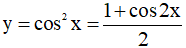 
tuần hoàn với chu kì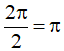 
Hàm số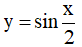 
tuần hoàn với chu kì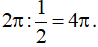 
Vậy hàm số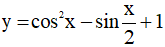 
tuần hoàn với chu kì T là bội chung nhỏ nhất của π và 4π, do đó T = 4π .
c) Ta có: y = sin4x.cos2x .
Hàm số y = sin6x tuần hoàn với chu kì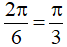 
Hàm số y = sin2x tuần hoàn với chu kì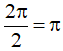 
Vậy hàm số y = sin4x.cos2x tuần hoàn với chu kì T là bội chung nhỏ nhất của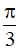 
và π, do đó T = π .
d) Hàm số y = sinx tuần hoàn với chu kì 2π .
Hàm số cos(√2x) tuần hoàn với chu kì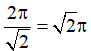 
Giả sử T là bội chung nhỏ nhất của 2π và √2π. Khi đó tồn tại m,n ∈ Z; m,n ≠ 0 sao cho: T = m2π = n√2π
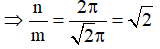(vô lí vì √2 là số vô tỉ, 
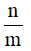là số hữu tỉ)
Do đó không tồn tại bội chung nhỏ nhất của 2π và √2π.
Vậy hàm số y = sinx + cos(√2x) không tuần hoàn.
3. Bài tập tự luyện
Câu 1. Cho hàm số f(x) = cot2x và g(x) = cos5x chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm số chẵn
B. f(x) là hàm số lẻ, g(x) là hàm số lẻ
C. f(x) là hàm số lẻ, g(x) là hàm số chẵn
D. f(x) là hàm số chẵn, g(x) là hàm số lẻ
Câu 2. Hàm số nào sau đây là hàm số chẵn?
A. y = sinx B. y = cos2x C. y = cotx D. y = tan3x
Câu 3. Hàm số nào sau đây là hàm số chẵn?
A. y = sin2x + cosx B. y = sinx – sin2x C. y = cot2x.cosx D. y = sinx.cos2x
Câu 4. Cho hàm số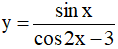 
. Khẳng định nào sau đây là đúng
A. Hàm số là hàm số lẻ B. Hàm số là hàm số chẵn
C. Hàm số không chẵn không lẻ D. Hàm số có tập xác định D = R\
Câu 5. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A. sinx.cos3x B.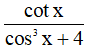 
C. cosx + sin2x D. |cot4x|
Câu 6. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
Câu 7. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
Câu 8. Hàm số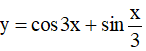 
tuần hoàn với chu kì?
A. 6π B. π C. 3π D.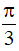 
Câu 9. Hàm số y = sin2x tuần hoàn với chu kì?
A. 2π B. 4π C.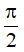 
D. π
Câu 10. Hàm số y = tanx + cot4x tuần hoàn với chu kì?
A.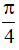 
B. 4π C. 
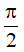D. π
Câu 11. Hàm số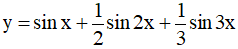 
tuần hoàn với chu kì?
A. 4π B. 2π C. π D. 6π
Câu 12. Hàm số y = 2cos2(πx) + 1 tuần hoàn với chu kì?
A. 1 B. 2 C. 3 D. 4
Câu 13. Hàm số y = 3sinx.cos3x + 1 tuần hoàn với chu kì:
A.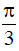 
B. 2π C. 
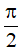D. π
Câu 14. Trong các hàm số sau, hàm số nào nào không tuần hoàn:
A. y = tan22x + 1 B. y = sin5x – 4cos7x
C. y = sinx + sin(x√2) D. y = 3sin2x - √2
Câu 15. Trong các hàm số sau, hàm số nào là hàm số tuần hoàn?
A. y = sin x – x B. y = -2cos3x + 2
C. y = xsin2x D. y = x4 + x2 + 1
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
C |
B |
A |
A |
D |
B |
B |
A |
D |
D |
C |
A |
D |
C |
B |
Phần 3: Phương pháp tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác
1. Lý thuyết
a) Cho hàm số y = f(x) xác định trên miền D ⊂ R .
- Số thực M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu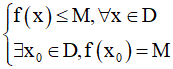 
- Số thực m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu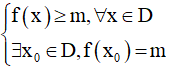 
b) Tính bị chặn của hàm số lượng giác:
-1 ≤ sin x ≤ 1∀x ∈ R
-1 ≤ cos x ≤ 1∀x ∈ R
2. Các dạng bài tập
Dạng 1. Sử dụng tính bị chặn của hàm số lượng giác
Phương pháp giải:
-1 ≤ sin [u(x)] ≤ 1; 0 ≤ sin2[u(x)] ≤ 1; 0 ≤ |sin[u(x)]| ≤ 1
-1 ≤ cos [u(x)] ≤ 1; 0 ≤ cos2[u(x)] ≤ 1; 0 ≤ |cos[u(x)]| ≤ 1
Ví dụ minh họa:
Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của các hàm số:
a) y = sin2x + 3
b) y = 4sin2xcos2x +1
c) y = 5 – 3cos23x
Lời giải
a) Ta có: -1 ≤ sin 2x ≤ 1 ∀x ∈ R
⇔ 2 ≤ sin 2x + 3 ≤ 4 ∀x ∈ R
Vậy hàm số y = sin2x + 3 có giá trị lớn nhất là 4 và giá trị nhỏ nhất là 2.
b) y = 4sin2xcos2x +1 = 2sin4x + 1
Ta có: -1 ≤ sin 4x ≤ 1 ∀x ∈ R
⇔ -2 ≤ 2sin 4x ≤ 2 ∀x ∈ R
⇔ -1 ≤ 2sin 4x + 1 ≤ 3 ∀x ∈ R
Vậy hàm số y = 4sin2xcos2x +1 có giá trị lớn nhất là 3 và giá trị nhỏ nhất là -1.
c) Ta có: 0 ≤ cos23x ≤ 1 ∀x ∈ R
⇔ 0 ≤ 3cos23x ≤ 3 ∀x ∈ R
⇔ -3 ≤ -3cos23x ≤ 0 ∀x ∈ R
⇔ 2 ≤ 5 - 3cos23x ≤ 5 ∀x ∈ R
Vậy hàm số y = 5 – 3cos23x có giá trị lớn nhất là 5 và giá trị nhỏ nhất là 2.
Ví dụ 2: Tìm giá trị lớn nhất và nhỏ nhất của các hàm số:
a) y =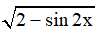 
b) y = cos2x + 4sinx - 5
c) y = 4|cos(3x-1)| + 1
Lời giải
a) Điều kiện xác định: 2 - sin2x ≥ 0 ⇔ sin 2x ≤ 2 (Luôn đúng với mọi x)
Tập xác định D = R.
Ta có: -1 ≤ sin 2x ≤ 1 ∀x ∈ R
⇔ -1 ≤ -sin 2x ≤ 1 ∀x ∈ R
⇔ 1 ≤ 2 - sin 2x ≤ 3 ∀x ∈ R
⇔ 1 ≤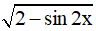
≤ √3∀x ∈ R
Vậy hàm số y =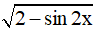 
có giá trị lớn nhất là √3 và giá trị nhỏ nhất là 1.
b) y = cos2x + 4sinx – 5
= 1 – 2sin2x + 4sinx – 5
= -2sin2x + 4sinx – 4
= -2(sin2x – 2sinx + 1) – 2
= -2(sinx – 1)2 – 2
Ta có: -1 ≤ sinx ≤ 1 ∀x ∈ R
⇔ -2 ≤ sinx - 1 ≤ 0 ∀x ∈ R
⇔ 0 ≤ (sinx - 1)2 ≤ 4 ∀x ∈ R
⇔ -8 ≤ -2(sinx - 1)2 ≤ 0 ∀x ∈ R
⇔ -10 ≤ -2(sinx - 1)2 - 2 ≤ -2 ∀x ∈ R
Vậy hàm số y = cos2x + 4sinx – 5 có giá trị lớn nhất là -2 và giá trị nhỏ nhất là -10.
c) Ta có: 0 ≤ |cos(3x-1)| ≤ 1 ∀x ∈ R
⇔ 0 ≤ 4|cos(3x-1)| ≤ 4 ∀x ∈ R
⇔ 1 ≤ 4|cos(3x-1)| + 1≤ 5 ∀x ∈ R
Vậy hàm số y = 4|cos(3x-1)| + 1 có giá trị lớn nhất là 5 và giá trị nhỏ nhất là 1.
Dạng 2. Hàm số có dạng y = asinx + bcosx + c (với a, b khác 0)
Phương pháp giải:
Bước 1: Ta đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]:
y = asinx + bcosx + c =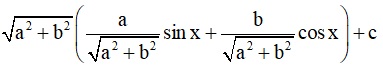 
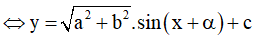với α thỏa mãn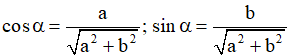 
Bước 2: Đánh giá -1 ≤ sin (x + α) ≤ 1 ∀x ∈ R
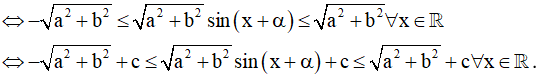
Ví dụ minh họa:
Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:
a) y = sin2x - √3cos2x + 1
b) y = 3sinx + 4cosx + 6
Lời giải
Vậy hàm số y = sin2x - √3cos2x + 1 có giá trị lớn nhất là 3 và giá trị nhỏ nhất là -1.
b) y = 3sinx + 4cosx + 6 =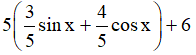 
Đặt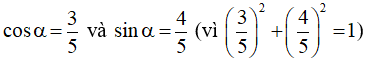 
Ta được: y = 5(sinxcosα + cosxsinα) + 6 = 5(sinx + α) + 6
Ta có: -1 ≤ sin (x + α) ≤ 1 ∀x ∈ R
⇔ -5 ≤ 5sin (x + α) ≤ 5 ∀x ∈ R
⇔ 1 ≤ 5sin (x + α) + 6 ≤ 11 ∀x ∈ R
Vậy hàm số y = 3sinx + 4cosx + 6 có giá trị lớn nhất là 11 và giá trị nhỏ nhất là 1.
Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số √3sin2x + sin2x - cos2x + 1
Lời giải
y = √3sin2x + sin2x - cos2x + 1
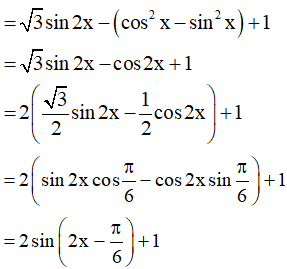
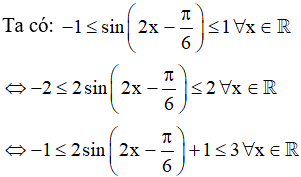
Vậy hàm số có giá trị lớn nhất là 3 và giá trị nhỏ nhất là -1.
Dạng 3: Hàm số có dạng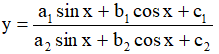 
Lý thuyết: Phương trình asinx + bcosx = c có nghiệm khi a2 + b2 ≥ c2 (Lý thuyết có trong phần 7)
Phương pháp giải:
Bước 1: Điều kiện xác định: a2sinx + b2cosx = c2 ≠ 0
Bước 2: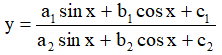 
⇔ ya2sinx + yb2cosx + yc2 = a1sinx + b1cosx + c1
⇔ (ya2 - a1)sinx + (yb2 - b1)cosx = -yc + c1 (*)
Bước 3: Để phương trình (*) có nghiệm x thì (ya2 - a1)2 + (yb2 - b1)2 ≥ (-yc + c1)2
Tìm đoạn chứa y, sau đó đưa ra kết luận về giá trị lớn nhất và giá trị nhỏ nhất.
Ví dụ minh họa:
Ví dụ 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: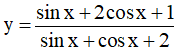 
Lời giải
Điều kiện xác định: sinx + cosx + 2 ≠ 0
Ta có:
sinx + cosx + 2
=
.
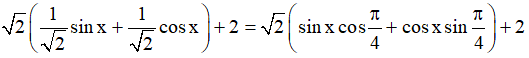
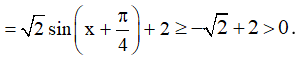Do đó sinx + cosx + 2 ≠ 0 ∀x∈ R
Tập xác định: D = R.
Ta có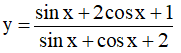 
⇔ ysinx + ycosx + 2y = sinx + 2cosx + 1
⇔ (y - 1)sinx + (y - 2)cosx = 1 - 2y (*)
Để phương trình (*) có nghiệm x thì (y - 1)2 + (y - 2)2 ≥ (1 - 2y)2
⇔ y2 - 2y + 1 + y2 - 4y + 4 ≥ 1 - 4y + 4y2
⇔ 2y2 + 2y - 4 ≤ 0
⇔ 2(y - 1)(y + 2) ≤ 0
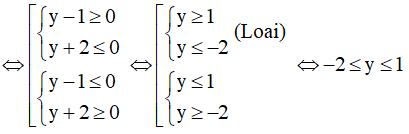
Vậy hàm số có giá trị lớn nhất là 1 và giá trị nhỏ nhất là -2.
Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: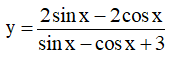 
Lời giải
Điều kiện xác định: sinx – cosx + 3 ≠ 0
Ta có: sinx – cosx + 3
.
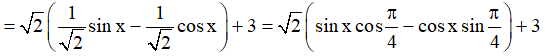
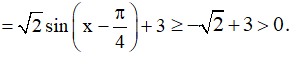Do đó sinx – cosx + 3 ≠ 0 ∀x ∈ R
Tập xác định: D = R.
Ta có: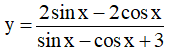 
⇔ ysinx - ycosx + 3y = 2sinx - 2cosx
⇔ (y - 2)sinx - (y + 2)cosx = - 3y (*)
Để phương trình (*) có nghiệm x thì (y - 2)2 + (y + 2)2 ≥ (-3y)2
⇔ y2 - 4y + 4 + y2 + 4y + 4 ≥ 9y2
⇔ 7y2 ≤ 8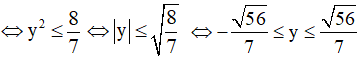 
Vậy hàm số có giá trị lớn nhất là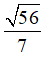 
và giá trị nhỏ nhất là -
.
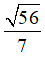3. Bài tập tự luyện
Câu 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=2sin5x – 1
A. min y = -3, max y = 3 B. min y = -1, max y = 1
C. min y = -1, max y=3 D. min y = -3, max y = 1
Câu 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 1 + cos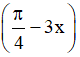
A. min y = -2, max y = 4 B. min y = 2, max y = 4
C. min y = -2, max y = 3 D. min y = -1, max y = 4
Câu 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số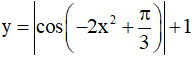 
A. max y = 1, min y = 0 B. max y = 2, min y = 0
C. max y = 1, min y = -1 D. max y = 2, min y = 1
Câu 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số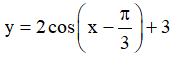 
A. min y = 2, max y = 5 B. min y = 1, max y = 4
C. min y = 1,max y = 5 D. min y = 1, max y = 3
Câu 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
A. max y = √5, min y = 1 B. max y = √5 , min y = 2√5
C. max y = √5, min y = 2 D. max y = √5 , min y = 3
Câu 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số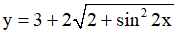 
A. min y = 3 + 2√2 , max y = 3 + 2√3 B. min y = 2 + 2√2 , max y = 3 + 2√3
C. min y = 3 - 2√2 , max y = 3 + 2√3 D. min y = 3 + 2√2 , max y = 3 + 3√3
Câu 7. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 – 2cos23x
A. min y = 1, max y = 2 B. min y = 1, max y = 3
C. min y = 2, max y = 3 D. min y = -1, max y = 3
Câu 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = sin2x – 4sinx + 5
A. max y = 9, min y = 2 B. max y = 10, min y = 2
C. max y = 6, min y = 1 D. max y = 5, min y = 1
Câu 9. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos2x + 4cosx – 2
A. max y = 3, min y = -7 B. max y = -1, min y = -5
C. max y = 4, min y = -1 D. max y = 3, min y = -5
Câu 10. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sin x + 4cosx + 1
A. max y = 6, min y = -2 B. max y = 4, min y = -4
C. max y = 6, min y = -4 D. max y = 6, min y = -1
Câu 11. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = √3 cosx + sinx + 4
A. min y = 2, max y = 4 B. min y = 2, max y = 6
C. min y = 4, max y = 6 D. min y = 2, max y = 8
Câu 12. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin 6x + 3cos 6x
A. min y = -5, max y = 5 B. min y = -4, max y = 4
C. min y = -3, max y = 5 D. min y = -6, max y = 6
Câu 13. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2sin2x + 3sin2x – 4cos2x
A. min y = -3√2 - 1, max y = 3√2 + 1 B. min y = -3√2 - 1, max y = 3√2 - 1
C. min y = -3√2, max y = 3√2 - 1 D. min y = -3√2 - 2, max y = 3√2 - 1
Câu 14. Giá trị lớn nhất của hàm số 
là
A. 1 B. √2
C.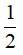 
D. 2
Câu 15. Gọi M, m lần lượt là giá trị nhỏ nhất của hàm số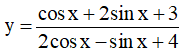 
. Giá trị của M+m là:
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
D |
A |
D |
C |
A |
A |
B |
B |
D |
C |
B |
A |
B |
A |
B |
Phần 4: Phương pháp giải phương trình lượng giác cơ bản
1. Lý thuyết
a) Phương trình sin x = m
Trường hợp 1: |m| > 1. Phương trình vô nghiệm.
Trường hợp 2: |m| ≤ 1 . Phương trình có nghiệm.
- Nếu m biểu diễn được dưới dạng sin của những góc đặc biệt thì:
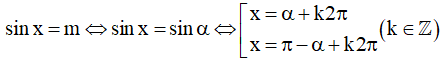
- Nếu m không biểu diễn được dưới dạng sin của những góc đặc biệt thì:
- Các trường hợp đặc biệt:
sin x = 0 ⇔ x = kπ (k ∈ Z)
sin x = 1 ⇔ x =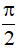 
+ k2π (k ∈ Z)
sin x = -1 ⇔ x = -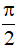
+ k2π (k ∈ Z)
b) Phương trình cos x = m
Trường hợp 1: |m| > 1. Phương trình vô nghiệm.
Trường hợp 2: |m| ≤ 1 . Phương trình có nghiệm.
- Nếu m biểu diễn được dưới dạng cos của những góc đặc biệt thì:
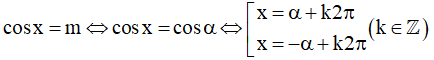
- Nếu m không biểu diễn được dưới dạng cos của những góc đặc biệt thì:
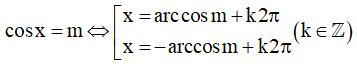
- Các trường hợp đặc biệt:
cos x = 0 ⇔ x = 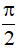+ k2π (k ∈ Z)
cos x = 1 ⇔ x = k2π (k ∈ Z)
cos x = -1 ⇔ x = π + kπ (k ∈ Z)
c) Phương trình: tan x = m. Điều kiện: x ≠ 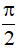+ k2π (k ∈ Z)
- Nếu m biểu diễn được dưới dạng tan của những góc đặc biệt thì:
tan x = m ⇔ tan x = tan α ⇔ x = α + kπ (k ∈ Z)
- Nếu m không biểu diễn được dưới dạng tan của những góc đặc biệt thì:
tan x = m ⇔ x = αrctan m + kπ (k ∈ Z)
d) Phương trình: cot x = m. Điều kiện: x ≠ kπ(k ∈ Z)
- Nếu m biểu diễn được dưới dạng cot của những góc đặc biệt thì:
cot x = m ⇔ cot x = cot α ⇔ x = α + kπ (k ∈ Z)
- Nếu m không biểu diễn được dưới dạng cot của những góc đặc biệt thì:
cot x = m ⇔ x = αrccot m + kπ (k ∈ Z)
e) Chú ý:
Nếu gặp bài toán yêu cầu tìm số đo độ của góc lượng giác sao cho sin (cos, tan, cot) của chúng bằng m.
Ví dụ: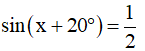 
ta có thể áp dụng các công thức nghiệm nêu trên, lưu ý sử dụng kí hiệu số đo độ trong công thức nghiệm.
Đối với ví dụ trên ta viết: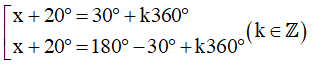 
chứ không viết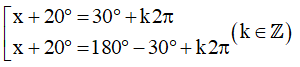 
2. Phương pháp giải:
Sử dụng công thức nghiệm cơ bản của phương trình lượng giác.
Mở rộng công thức nghiệm, với u(x) và v(x) là hai biểu thức của x.
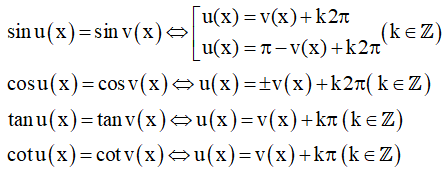
3. Ví dụ minh họa
Ví dụ 1: Giải các phương trình sau:
a)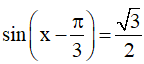 
b) 3cos(x+1) = 1
c) tan(3x + 150) = √3
d)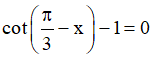 
Lời giải
a)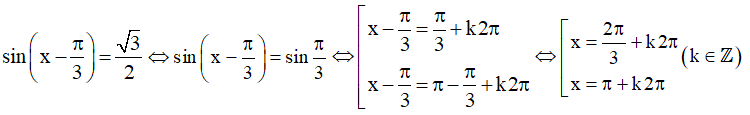 
Vậy họ nghiệm của phương trình là: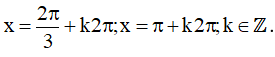 
b) 3cos(x+1) = 1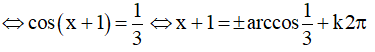 
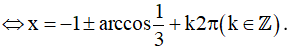
Vậy họ nghiệm của phương trình là: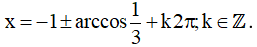 
c) Điều kiện xác định: cos(3x + 150) ≠ 0
⇔ 3x + 150 ≠ 900 + k180
⇔ 3x ≠ 750 + k180
⇔ x ≠ 250 + k600 (k ∈ Z)
Ta có: tan(3x + 150) = √3
⇔ tan(3x + 150) = tan600
⇔ 3x + 150 = 600 + k180
⇔ x = 150 + k600 (k ∈ Z) (Thỏa mãn)
Vậy họ nghiệm của phương trình là: x = 150 + k600 (k ∈ Z)
d) Điều kiện xác định: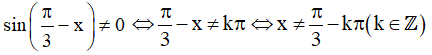 
⇔ 
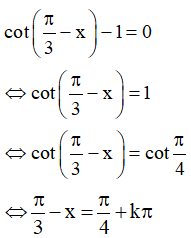
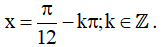(Thỏa mãn)
Vậy họ nghiệm của phương trình là: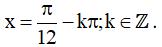 
Ví dụ 2: Giải các phương trình sau:
a)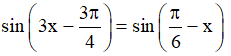 
b) cos5x – sinx = 0
c)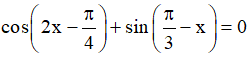 
d)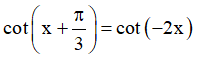 
Lời giải
a)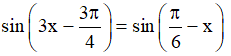 
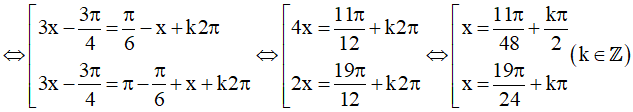
Vậy họ nghiệm của phương trình là: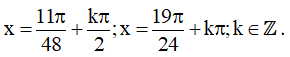 
b) cos5x – sinx = 0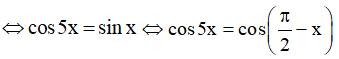 
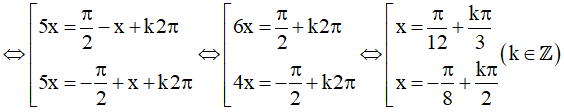
Vậy họ nghiệm của phương trình là: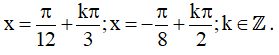 
c)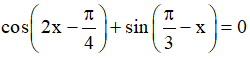 
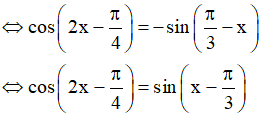
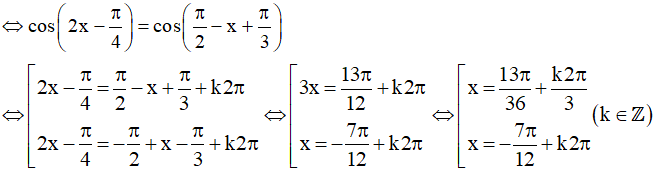
Vậy họ nghiệm của phương trình là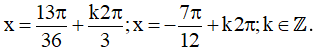 
d) Điều kiện xác định: 
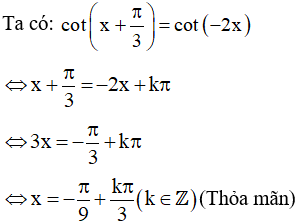
Vậy họ nghiệm của phương trình là: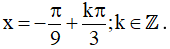 
Ví dụ 3: Giải các phương trình sau:
a) (1 + 2cosx)(3 – cosx) = 0
b) (cotx + 1)sin3x = 0
c)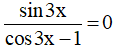 
d) tanx.tan2x = 1
Lời giải
a) (1 + 2cosx)(3 – cosx) = 0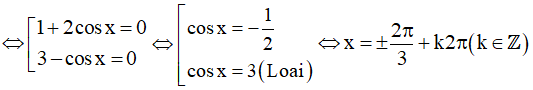 
Vậy họ nghiệm của phương trình là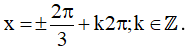 
b) Điều kiện xác định: sinx ≠ 0 ⇔ x ≠ kπ(k ∈ Z)
Ta có: (cotx + 1)sin3x = 0
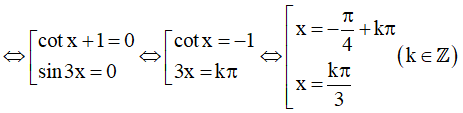
Kết hợp với điều kiện xác định ta được họ nghiệm của phương trình là: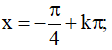 
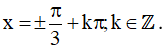
c) Điều kiện xác định: cos3x - 1 ≠ 0 ⇔ cos3x ≠ 1 ⇔ 3x ≠ k2π ⇔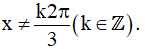 
.
Ta có: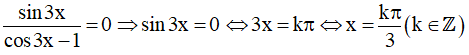 
Kết hợp với điều kiện xác định ta được họ nghiệm của phương trình là: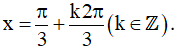 
d) Điều kiện xác định: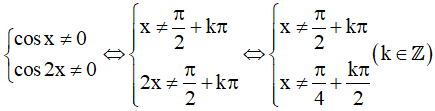 
tanx.tan2x = 1 (*)
Trường hợp 1: tanx = 0. Thay vào (*) (vô lí).
Trường hợp 2: tanx ≠ 0 ⇔ x ≠ kπ (k ∈ Z)
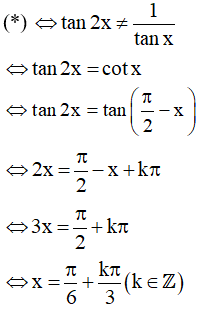
Kết hợp với điều kiện xác định ta được họ nghiệm của phương trình là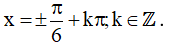 
4. Bài tập tự luyện
Câu 1. Họ nghiệm của phương trình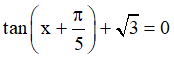 
là
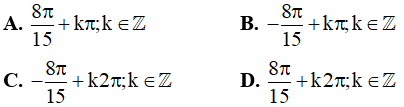
Câu 2. Số nghiệm của phương trình: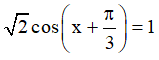 
với 0 ≤ x ≤ 2π là :
A. 0 B. 2 C. 1 D. 3
Câu 3. Các nghiệm phương trình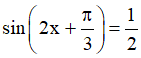 
là:
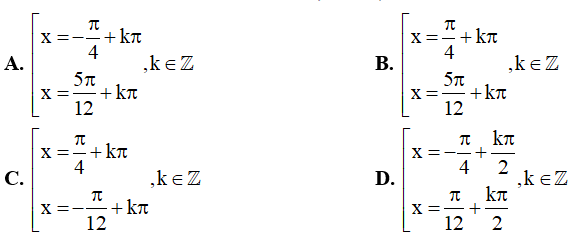
Câu 4. Các nghiệm của phương trình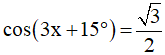 
là:
Câu 5. Nghiệm của phương trình 2sinx.cosx = 1 là:
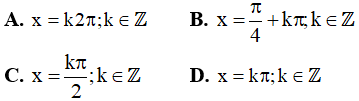
Câu 6. Phương trình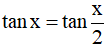 
có họ nghiệm là:
A. x = k2π,k ∈ Z B. x = kπ,k ∈ Z C. x = π + k2π,k ∈ Z D. x =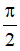 
+ kπ,k ∈ Z
Câu 7. Nghiệm của phương trình sin3x = cosx là:
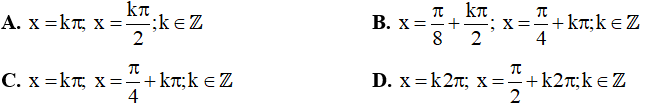
Câu 8. Nghiệm âm lớn nhất và nghiệm dương nhỏ của phương trình sin 4x + cos5x = 0 theo thứ tự là:
Câu 9. Giải phương trình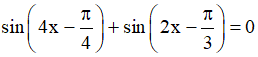 
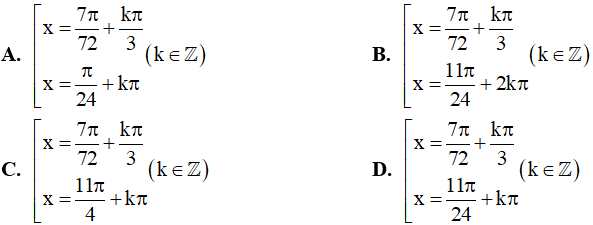
Câu 10. Nghiệm của phương trình sinx(2cosx - √3) = 0 là:
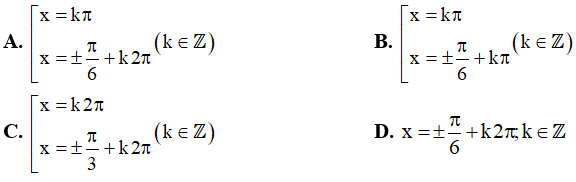
Câu 11. Nghiệm của phương trình tanx = cotx
Câu 12. Nghiệm của phương trình tan3x.cot2x = 1 là
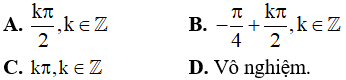
Câu 13. Phương trình (sinx + 1)(sinx - √2) = 0 có các nghiệm là:
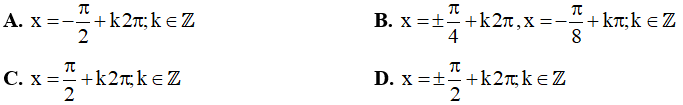
Câu 14. Giải phương trình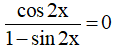 
Câu 15. Tìm tổng các nghiệm của phương trình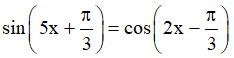 
trên [0,π]
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
B |
B |
C |
D |
B |
A |
B |
C |
D |
A |
A |
D |
A |
D |
D |
Phần 5: Tất tần tật về phương trình bậc nhất đối với hàm số lượng giác
1. Lý thuyết
Nhắc lại công thức nghiệm phương trình lượng giác
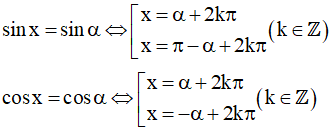
tanx = tan α ⇔ x = α + kπ(k ∈ Z)
cotx = cot α ⇔ x = α + kπ(k ∈ Z)
2. Các dạng bài tập
Dạng 1: Phương trình lượng giác sử dụng phân tích đa thức thành nhân tử đưa về phương trình tích
Phương pháp giải:
Sử dụng các biến đổi thích hợp để xuất hiện nhân tử chung như công thức nhân đôi, công thức nhân ba...
- Công thức nhân đôi:
sin2a = 2sina.cosa
cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
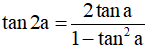
- Công thức nhân ba:
sin3a = 3sina – 4sin3a
cos3a = 4cos3a – 3cosa
Ví dụ minh họa:
Ví dụ 1: Giải các phương trình sau:
a) cosx – 2sin2x = 0
b) 6sin4x + 5sin8x = 0
c) cos2x – sin2x = 0
Lời giải
a) cosx – 2sin2x = 0
⇔ cosx - 2.2.sinxcosx = 0
⇔ cosx(1 - 4sinx) = 0
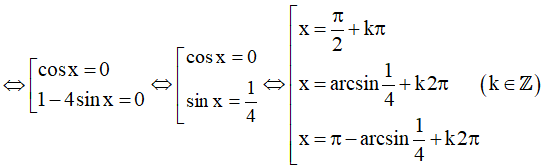
Vậy họ nghiệm của phương trình là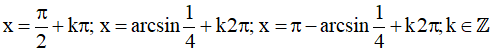 
b) 6sin4x + 5sin8x = 0
⇔ 6sin4x + 5.2.sin4xcos4x = 0
⇔ 2sin4x(3 + 5cos4x) = 0
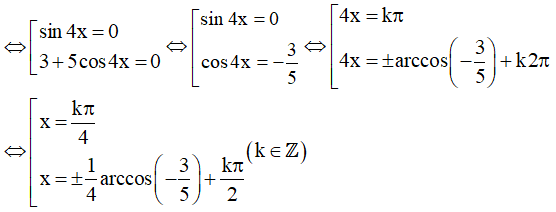
Vậy họ nghiệm của phương trình là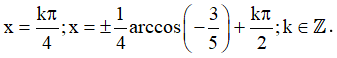 
c) cos2x – sin2x = 0
⇔ cos2x – 2sinxcosx = 0
⇔ cosx(cos x - 2sinx) = 0
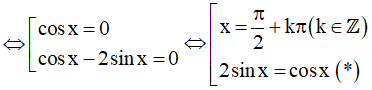
Giải phương trình (*)
Trường hợp 1: cosx = 0. Thay vào (*) ta được sinx = 0
Ta thấy sin2x + cos2x = 02 + 02 = 0 (Vô lí) (Loại).
Trường hợp 2: cosx ≠ 0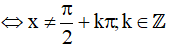 
Chia hai vế của phương trình cho cosx, ta được
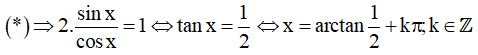(Thỏa mãn)
Vậy họ nghiệm của phương trình là: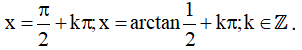
Ví dụ 2: Giải phương trình: sinx.cos3x – sinx + 2cos3x – 2 = 0.
Lời giải
Ta có: sinx.cos3x – sinx + 2cos3x – 2 = 0
⇔ sinx(cos3x - 1) + 2(cos3x - 1) = 0
⇔ (cos3x - 1)(sinx + 2) = 0
.
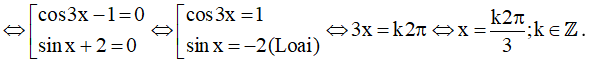Vậy họ nghiệm của phương trình là: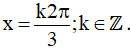 
Dạng 2: Sử dụng công thức biến đổi tổng thành tích và tích thành tổng
Phương pháp giải:
- Công thức biến đổi tổng thành tích
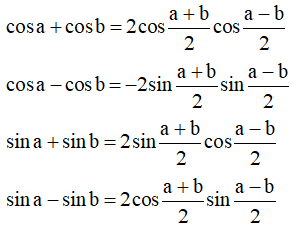
- Công thức biến đổi tích thành tổng
cosa.cosb =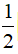 
[cos(a + b) + cos(a + b)]
sina.sinb =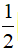 
[cos(a - b) - cos(a + b)]
sina.cosb =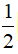 
[sin(a + b) + sin(a - b)]
Ví dụ minh họa:
Ví dụ 1: Giải các phương trình sau:
a) sin2x.sin5x = sin3x.sin4x
b) sin5x.cos3x = sin4x.cos2x
Lời giải
a) sin2x.sin5x = sin3x.sin4x
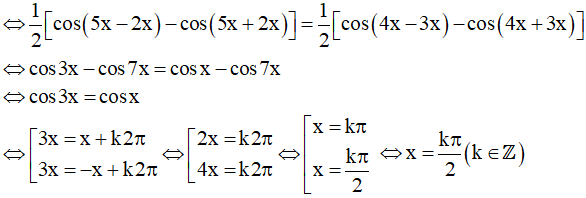
Vậy họ nghiệm của phương trình là: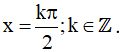 
b) sin5x.cos3x = sin4x.cos2x
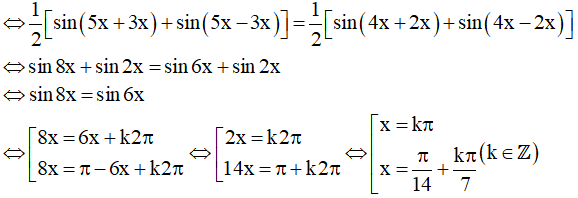
Vậy họ nghiệm của phương trình là: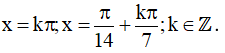 
Ví dụ 2: Giải các phương trình sau:
a) sin3x + sin2x = sinx
b) sinx + sin3x = cos2x + cos4x
Lời giải
a) sin3x + sin2x = sinx
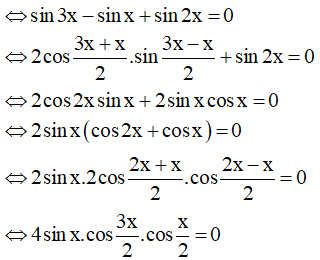
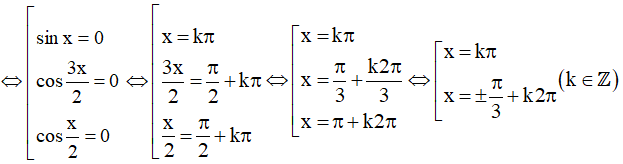
Vậy họ nghiệm của phương trình là: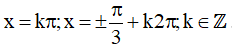 
b) sinx + sin3x = cos2x + cos4x
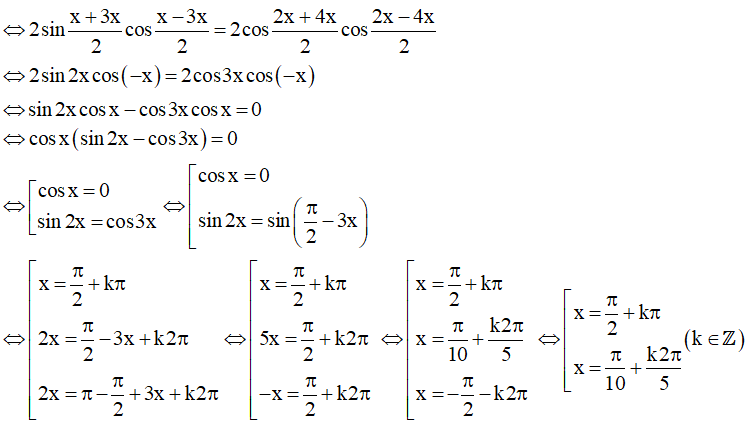
Vậy họ nghiệm của phương trình là: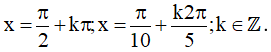 
Dạng 3: Sử dụng công thức hạ bậc
Phương pháp giải:
Công thức hạ bậc hai:
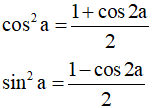
Ví dụ minh họa:
Ví dụ 1: Giải phương trình sau: sin2x + sin23x = 2sin22x.
Lời giải
Ta có: sin2x + sin23x = 2sin22x
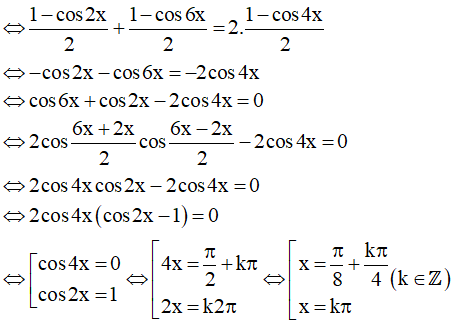
Vậy họ nghiệm của phương trình là: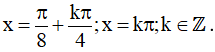 
Ví dụ 2: Giải phương trình sau: cos2x + cos22x + cos23x + cos24x = 2
Lời giải
Ta có: cos2x + cos22x + cos23x + cos24x = 2
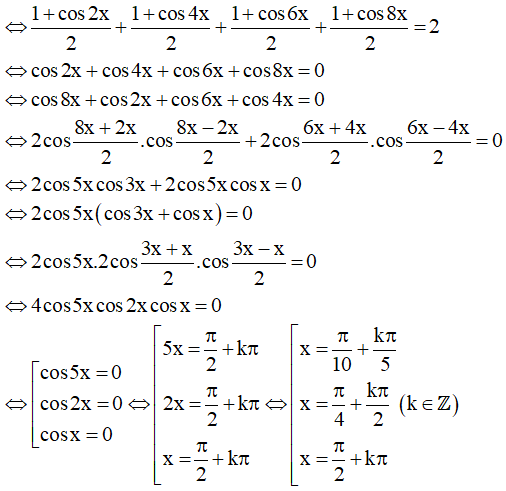
Vậy họ nghiệm của phương trình là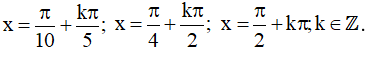 
3. Bài tập tự luyện
Câu 1. Nghiệm của phương trình cos2x – cosx = 0 thuộc khoảng 0 < x < π là:
Câu 2. Giải phương trình cos2x – sin2x = 0
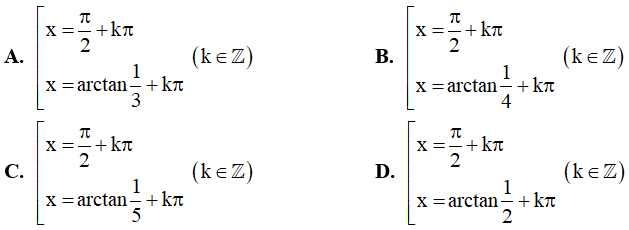
Câu 3. Nghiệm của phương trình sin2x – sinx = 2 – 4cosx là:
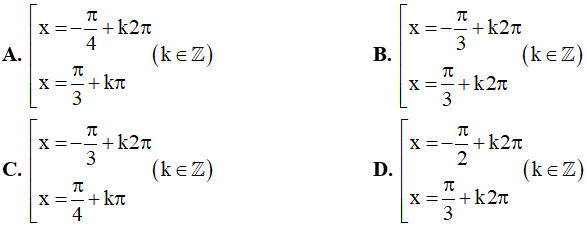
Câu 4. Nghiệm của phương trình sin x.cos x.cos2x = 0 là:
Câu 5. Nghiệm của phương trình cos3x – cos5x = sinx là:
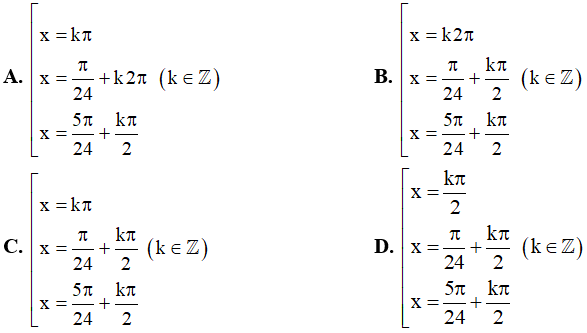
Câu 6. Phương trình cos5x.cos3x = cos 4x.cos2x có tập nghiệm trùng với tập nghiệm của phương trình nào sau đây?
A. sinx = cos x B. cosx = 0 C. cos8x = cos6x D. sin8x = cos6x
Câu 7. Phương trình cosx + 3cos2x + cos3x = 0 có nghiệm là:
Câu 8. Nghiệm của phương trình cos3x – cos4x + cos5x = 0 là:
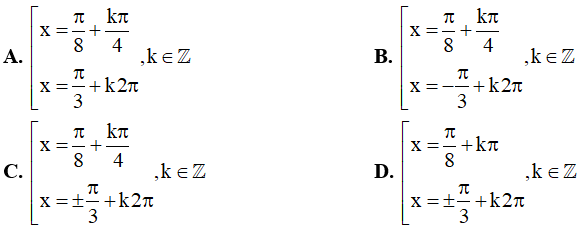
Câu 9. Phương trình 2sinx + cosx – sin2x – 1 = 0 có nghiệm là:
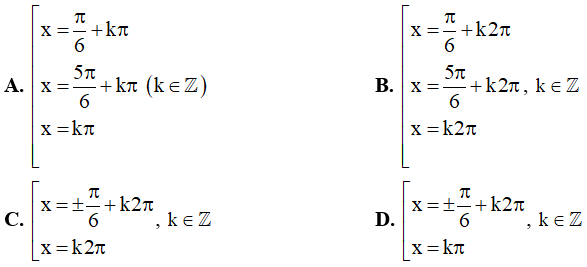
Câu 10. Một họ nghiệm của phương trình cos x.sin23x – cosx = 0 là :
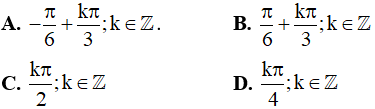
Câu 11. Các nghiệm của phương trình sin2x + sin23x = cos2x + cos23x là:
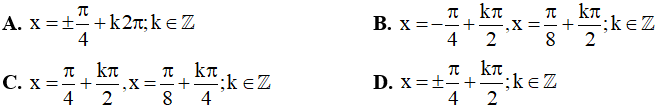
Câu 12. Các nghiệm của phương trình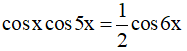 
(với k ∈ Z ) là:
Câu 13. Họ nghiệm của phương trình sin2x + cos24x = 1 là:
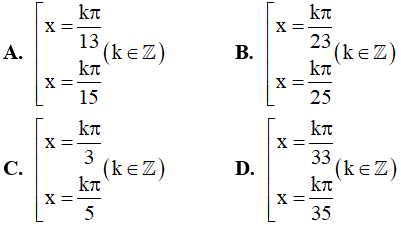
Câu 14. Họ nghiệm của phương trình cosx.cos7x = cos3x.cos5x là:
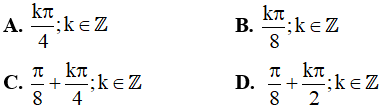
Câu 15. Phương trình sin23x – cos24x = sin25x – cos26x có các nghiệm là:
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
B |
D |
B |
D |
C |
C |
C |
C |
B |
B |
C |
D |
C |
A |
B |
Phần 6: Các bài toán về phương trình bậc hai của hàm số lượng giác và cách giải
1. Lý thuyết
Một số dạng phương trình bậc hai của một hàm số lượng giác
a. sin2x + b.sinx + c = 0 (a ≠ 0)
a. cos2x + b.cosx + c = 0 (a ≠ 0)
a. tan2x + b.tanx + c = 0 (a ≠ 0)
a. cot2x + b.cotx + c = 0 (a ≠ 0)
2. Phương pháp giải:
|
Phương trình dạng |
Điều kiện xác định |
Cách làm |
Điều kiện ẩn phụ (ẩn t) |
|
f(sinx) |
|
Đặt t = sinx |
-1 ≤ t ≤ 1 |
|
f(cosx) |
|
Đặt t = cosx |
-1 ≤ t ≤ 1 |
|
f(tanx) |
|
Đặt t = tanx |
|
|
f(cotx) |
x ≠ kπ; k ∈ Z |
Đặt t = cotx |
|
3. Ví dụ minh họa
Ví dụ 1: Giải các phương trình:
a) 2sin2x – 5sinx + 2 = 0
b) 5cos2x – 6cosx + 1 = 0
c) tan2x + 2tanx – 3 = 0
Lời giải
a) Đặt t = sinx với -1 ≤ t ≤ 1
Ta được phương trình: 2t2 – 5t + 2 = 0
⇔ 2t2 - 4t - t + 2 = 0 ⇔ (2t - 1)(t - 2) = 0
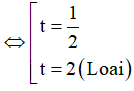
Khi đó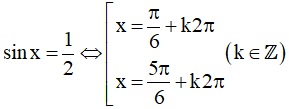 
Vậy họ nghiệm của phương trình là: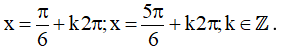 
b) Đặt t = cosx với -1 ≤ t ≤ 1
Ta được phương trình: 5t2 – 6t + 1 = 0
⇔ 5t2 – 5t - t + 1 = 0 ⇔ (5t - 1)(t - 1) = 0
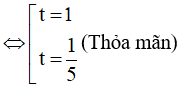
Khi đó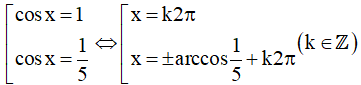 
Vậy họ nghiệm của phương trình là: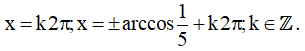 
c) Điều kiện xác định: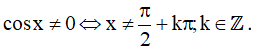 
Đặt t = tanx. Ta được phương trình: t2 + 2t – 3 = 0
⇔ t2 + 3t - t – 3 = 0
⇔ (t + 3)(t - 1) = 0
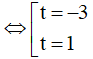
Khi đó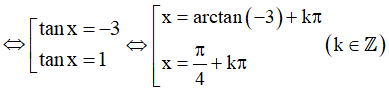 
(Thỏa mãn điều kiện xác định)
Vậy họ nghiệm của phương trình là: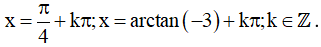
Ví dụ 2: Giải các phương trình:
a) sin2x + 2cosx + 2 = 0
b) cos2x – 4sinx = 3
c)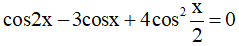 
Lời giải
a) sin2x + 2cosx + 2 = 0
⇔ 1 - cos2x + 2cosx + 2 = 0
⇔ - cos2x + 2cosx + 3 = 0
Đặt t = cosx với -1 ≤ t ≤ 1
Ta được phương trình: - t2 + 2t + 3 = 0
⇔ - (t + 1)(t - 3) = 0
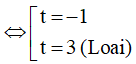
Khi đó cosx = -1 ⇔ x = π + k2π (k ∈ Z)
Vậy họ nghiệm của phương trình là: x = π + k2π (k ∈ Z)
b) cos2x – 4sinx = 3
⇔ 1 - sin2x - 4sinx - 3 = 0
⇔ - 2sin2x - 4sinx - 2 = 0
Đặt t = sinx với -1 ≤ t ≤ 1
Ta được phương trình: -2t2 – 4t – 2 = 0
⇔ -2(t + 1)2 = 0
⇔ t = -1 (Thỏa mãn)
Khi đó: sinx = -1 ⇔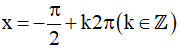 
Vậy họ nghiệm của phương trình là: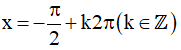 
c)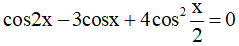 
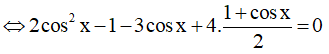
⇔ 2cos2x - cosx + 1 = 0
Đặt t = cosx với -1 ≤ t ≤ 1
Ta được phương trình: 2t2 – t + 1 = 0 (*)
Ta có: Δ = (-1)2 - 4.2.1 = -7 < 0. Do đó phương trình (*) vô nghiệm
Vậy phương trình đã cho vô nghiệm.
Ví dụ 3: Giải các phương trình:
a) tanx + 5cotx = 6
b)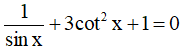 
Lời giải
a) Điều kiện xác định: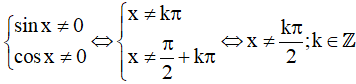 
Ta có: tanx + 5cotx = 6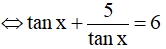 
Đặt t = tanx. Ta được phương trình: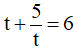 
(Điều kiện: t ≠ 0 )
⇔ t2 + 5 = 6t
⇔ t2 - 6t + 5 = 0
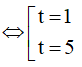
Khi đó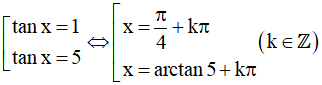 
Vậy họ nghiệm của phương trình là: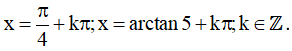 
b) Điều kiện xác định: sinx ≠ 0 ⇔ x ≠ kπ; k ∈ Z
Vì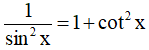 
nên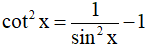 
Thay vào phương trình ta có: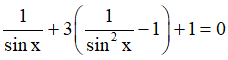
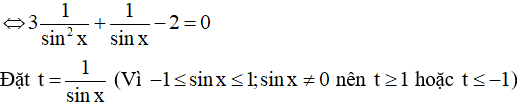
Ta được phương trình: 3t2 + t – 2 = 0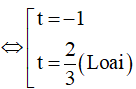 
Khi đó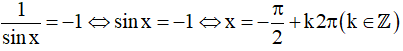 
Vậy họ nghiệm của phương trình là: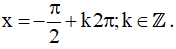 
4. Bài tập tự luyện
Câu 1. Nghiệm của phương trình lượng giác: 2cos2x + 3sinx – 3 = 0 thỏa mãn điều kiện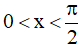 
là:
Câu 2. Các họ nghiệm của phương trình cos2x – sinx = 0 là:
Câu 3. Nghiệm dương bé nhất của phương trình: 2sin2x + 5sinx – 3 = 0 là:
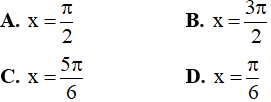
Câu 4. Nghiệm của phương trình 2cos2x + 2cosx - √2 = 0 là
Câu 5. Trong [0,2π) , phương trình sinx = 1 – cos2x có tập nghiệm là:
Câu 6. Có bao nhiêu nghiệm của phương trình cos4x + 3sin2x + 1 = 0 thuộc khoảng (0,2π) ?
A. 1 B. 2 C. 3 D. 4
Câu 7. Phương trình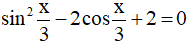 
có các nghiệm là:
A. x = kπ, k∈ Z B. x = k3π, k∈ Z C. x = k2π, k∈ Z D. x = k6π, k∈ Z
Câu 8. Họ nghiệm của phương trình 3cos4x + 2cos2x – 5 = 0 là:
A. k2π, k∈ Z B.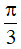 
+ k2π, k∈ Z C. kπ, k∈ Z D. -
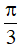+ k2π, k∈ Z
Câu 9. Phương trình tan2x + 5tanx – 6 = 0 có các nghiệm là:
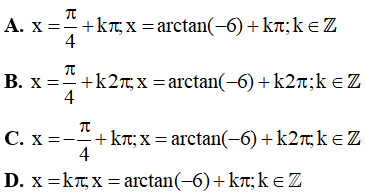
Câu 10. Một họ nghiệm của phương trình 3tan2x + 2cot2x - 5 = 0 là
Câu 11. Số nghiệm của phương trình 2tanx – 2cotx – 3 = 0 trong khoảng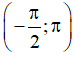 
là :
A. 2 B. 1 C. 4 D. 3
Câu 12. Phương trình cos2x + sin2x + 2cosx + 1 = 0 có nghiệm là:
Câu 13. Các nghiệm của phương trình √3tanx + cotx - √3 - 1 = 0 là:
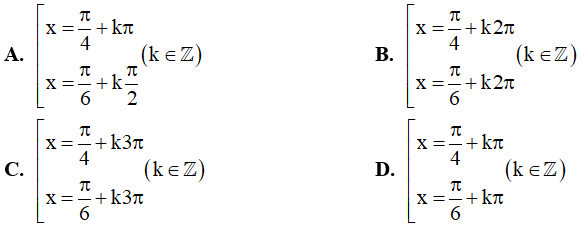
Câu 14. Số nghiệm của phương trình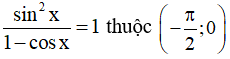 
là:
A. 2 B. 0 C. 1 D. 3
Câu 15. Họ nghiệm của phương trình cos2x + sinx + 1 = 0 là:
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
C |
C |
D |
A |
C |
D |
D |
C |
A |
D |
D |
D |
D |
B |
A |
Phần 7: Các bài toán về phương trình bậc nhất đối với sin và cos và cách giải
1. Lý thuyết
- Phương trình bậc nhất đối với sin và cos có dạng: a.sinx + b.cosx = c (với a; b là các số thực, a; b khác 0).
- Điều kiện có nghiệm: a2 + b2 ≥ c2 .
2. Các dạng bài tập
Dạng 1: Giải phương trình bậc nhất đối với sin và cos
- Phương pháp giải:
Chia cả hai vế của phương trình cho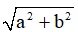 
, ta được:
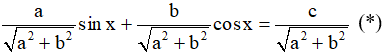
* Đặt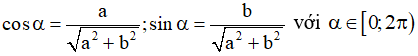 
Khi đó phương trình (*) đưa về dạng
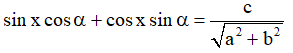
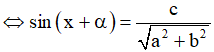. Đưa về phương trình lượng giác cơ bản.
* Hoặc đặt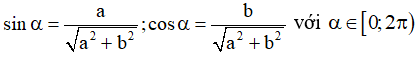 
Khi đó phương trình (*) đưa về dạng
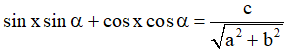
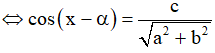. Đưa về phương trình lượng giác cơ bản.
* Phương trình có nghiệm khi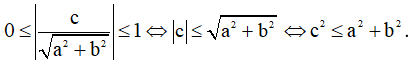 
Chú ý: Các công thức đặc biệt
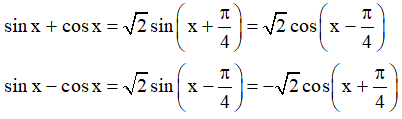
- Ví dụ minh họa:
Ví dụ 1: Giải các phương trình sau:
a) sin4x + √3cos4x = √2
b) 5sin2x +12cos2x = 13
c) sin2x - 2cosxsinx + 1 = 0
Lời giải
a) sin4x + √3cos4x = √2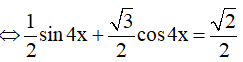 
(1)
Đặt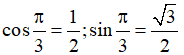 
Khi đó (1)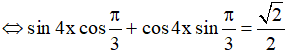 
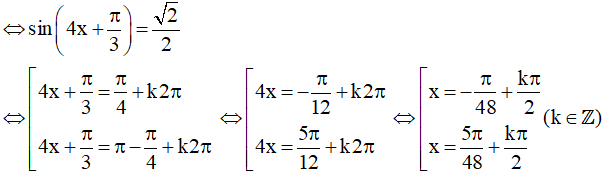
Vậy họ nghiệm của phương trình là: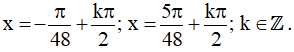 
b) 5sin2x +12cos2x = 13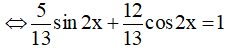 
(2)
Đặt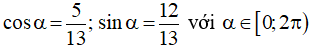 
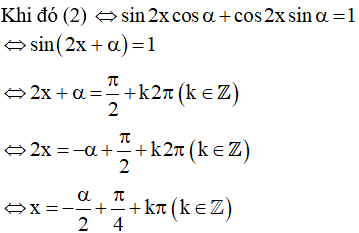
Vậy họ nghiệm của phương trình là: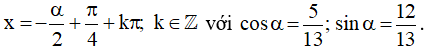 
c) sin2x - 2cosxsinx + 1 = 0
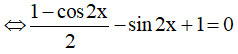
⇔ 1 - cos2x - 2sin2x + 2 = 0
⇔ cos2x + 2sin2x = 3
Ta thấy: 12 + 22 < 32. Vậy phương trình trên vô nghiệm.
Ví dụ 2: Giải các phương trình sau:
a) 3sin3x - √3cos9x = 1 + 4sin33x
b) cos3x - sin5x = √3(cos5x - sin3x)
Lời giải
a) 3sin3x - √3cos9x = 1 + 4sin33x
⇔ 3sin3x - 4sin33x - √3cos9x = 1
⇔ sin9x - √3cos9x = 1
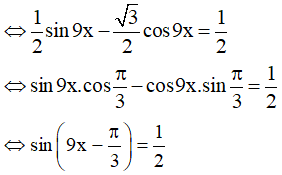
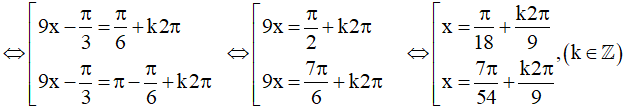
Vậy họ nghiệm của phương trình là: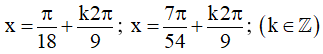 
b) cos3x - sin5x = √3(cos5x - sin3x)
⇔ cos3x - sin5x = √3cos5x - √3sin3x
⇔ cos3x + √3sin3x = √3cos5x + sin5x
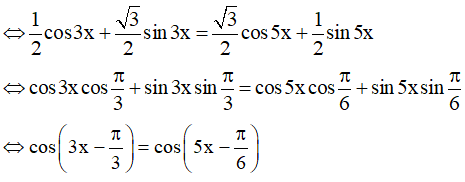
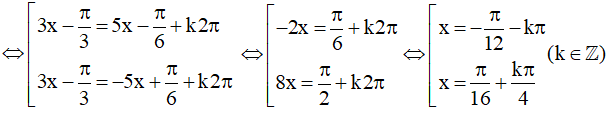
Vậy họ nghiệm của phương trình là: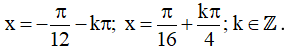 
Dạng 2: Tìm điều kiện để phương trình a.sinx + b.cosx = c có chứa tham số m có nghiệm
- Phương pháp giải:
Điều kiện có nghiệm: a2 + b2 ≥ c2
- Ví dụ minh họa:
Ví dụ 1: Tìm m để phương trình: (m-1)cosx + 2sinx = m+3 có nghiệm.
Lời giải
Để phương trình có nghiệm: (m-1)2 + 22 ≥ (m + 3)2
⇔ m2 - 2m + 1 + 4 ≥ m2 + 6m + 9
⇔ -8m ≥ 4
⇔ 
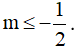
Vậy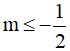 
thì phương trình (m-1)cosx + 2sinx = m+3 có nghiệm.
Ví dụ 2: Tìm m để phương trình: (m-1)sinx + mcosx = m+1 có nghiệm.
Lời giải
Để phương trình có nghiệm: (m-1)2 + m2 ≥ (m + 1)2
⇔ m2 - 2m + 1 + m2 ≥ m2 + 2m + 1
⇔ m2 - 4m ≥ 0
⇔ m (m - 4) ≥ 0
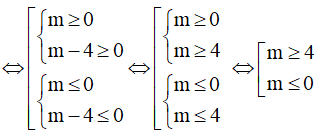
Vậy m ≥ 4 hoặc m ≤ 0 thì phương trình (m-1)sinx + mcosx = m+1 có nghiệm.
3. Bài tập tự luyện
Câu 1. Họ nghiệm của phương trình √3sin2x - cos2x + 1 = 0 là:
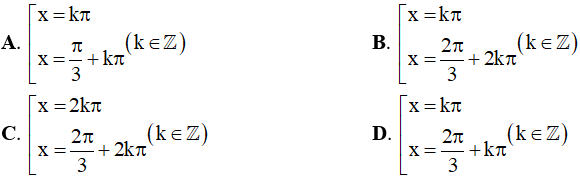
Câu 2. Có bao nhiêu nghiệm thuộc khoảng (0, 2π) của phương trình cos4x – sin4x = 1?
A. 5 B. 3 C. 6 D. 7
Câu 3. Họ nghiệm của phương trình: sin3x - √3cos3x = 2cos5x là:
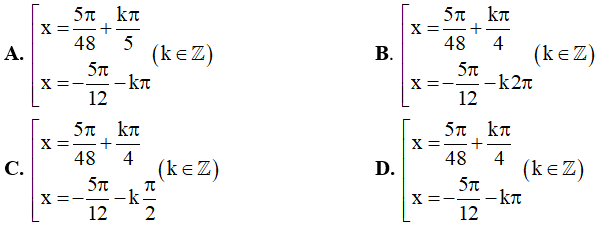
Câu 4. Tính tổng tất cả các nghiệm của phương trình cos2x - sin2x = √2 + sin2x trên khoảng (0, 2π)
Câu 5. Họ nghiệm của phương trình: √3(sin2x + cos5x) = sin5x - cos2x là:
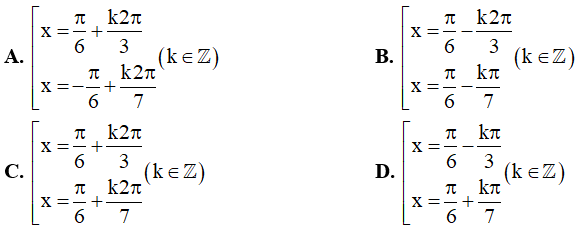
Câu 6. Các nghiệm của phương trình 1+ sin2x = cos 2x là:
Câu 7. Số nghiệm thuộc khoảng (0, π) của phương trình sinx(sinx + 2cosx) = 2 là
A. 0 B. 1 C. 2 D. 3
Câu 8. Tổng các nghiệm thuộc khoảng (-π, π) của phương trình sinx + cosx = 2√2sinxcosxlà:
Câu 9. Họ nghiệm của phương trình: 4(sin4x + cos4x) + √3sin4x = 2 là:
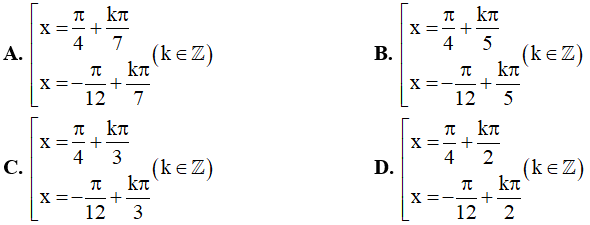
Câu 10. Họ nghiệm của phương trình: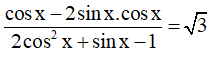
là:
Câu 11. Tìm tất cả các giá trị của m để phương trình 3sinx – 4cosx = 2m có nghiệm.
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để phương trình (m+1)sin2x – sin2x + cos2x = 0 có nghiệm?
A. 12 B. 13 C. 11 D. 10
Câu 13. Phương trình 2sinxcosx + √3cos2x + m = 0 có nghiệm khi và chỉ khi:
A. -2 ≤ m < 2 B. -2 ≤ m ≤ 2 C. m ≤ 2 D. -2 < m ≤ 2
Câu 14. Tìm m để phương trình (2m-1)cos2x + 2msinxcosx = m – 1 vô nghiệm.
Câu 15. Gọi M, m lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = √3sin3x - cos3x + 2. Giá trị của M, m là:
A. M = 4; m = 0 B. M = 2; m = -2 C.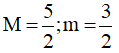 
D. M = 3; m = 1
Bảng đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
D |
D |
D |
D |
C |
C |
A |
B |
D |
D |
D |
A |
B |
D |
A |
Chuyên đề hàm số lượng giác và phương trình lượng giác
A. Tóm tắt lý thuyết
1. Hàm số sin
Định nghĩa: Qui tắc đặt tương ứng mỗi số thực x với số thực sinx
sin: R -> R
x \[ \mapsto \]sinx được gọi là hàm số sin,
Kí hiệu y = sinx
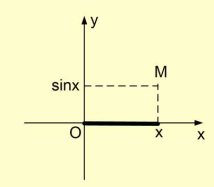
Tính chất:
Tập xác định \[\mathbb{R}\].
Tập giá trị: [-1;1] ,có nghĩa là -1 \[ \le \]sinx \[ \le \]1, \[\forall \]x \[ \in \]\[\mathbb{R}\] .
Hàm số tuần hoàn với chu kì \[2\pi \] , có nghĩa sin ( x + \[k2\pi \]) với k\[ \in \]\[\mathbb{Z}\].
Hàm số đồng biến trên mỗi khoảng \[\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\] và nghịch biến trên mỗi khoảng \[\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\] , k \[ \in \mathbb{Z}\] .
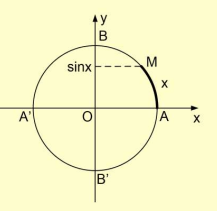
y = sin x là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng (Hình 1).
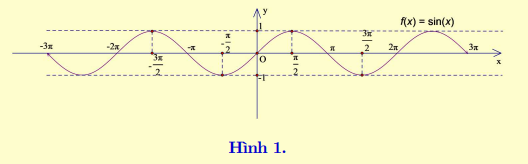
Một số giá trị đặc biệt
Sin x = 0 \[ \Leftrightarrow x = k\pi (k \in \mathbb{Z})\]
Sin x = 1 \[ \Leftrightarrow x = \frac{\pi }{2} + k2\pi (k \in \mathbb{Z})\]
Sin x = - 1 \[ \Leftrightarrow x = - \frac{\pi }{2} + k2\pi (k \in \mathbb{Z})\]
2. Hàm số cos
Định nghĩa: Qui tắc đặt tương ứng mỗi số thực x với số thực cosx
cos: R ® R
x \[ \mapsto \]cosx được gọi là hàm số cos,
Kí hiệu y = cosx
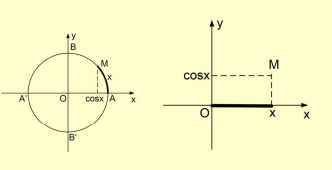
Tính chất:
Tập xác định \[\mathbb{R}\].
Tập giá trị: [-1;1] ,có nghĩa là -1 \[ \le \]cosx \[ \le \]1, \[\forall \]x \[ \in \]\[\mathbb{R}\] .
Hàm số tuần hoàn với chu kì \[2\pi \] , có nghĩa cos ( x + \[k2\pi \]) = cos x với k\[ \in \]\[\mathbb{Z}\].
Hàm số đồng biến trên mỗi khoảng \[\left( { - \pi + k2\pi ;k2\pi } \right)\] và nghịch biến trên mỗi khoảng \[\left( {k2\pi ;\pi + k2\pi } \right)\] , k \[ \in \mathbb{Z}\] .
y = cos x là hàm số chẵn, đồ thị hàm số nhận Oy là trục đối xứng (Hình 2).
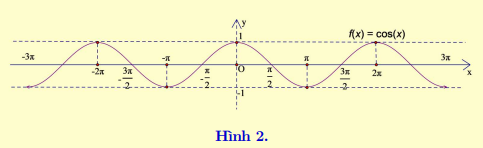
Ta có cos x = sin \[\left( {x + \frac{\pi }{2}} \right)\] nên đồ thị của hàm số y = cosx được suy ra từ đồ thị hàm số y = sinx bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto \[\overrightarrow u = \left( { - \frac{\pi }{2};0} \right)\]
Một số giá trị đặc biệt
cos x = 0 \[ \Leftrightarrow x = \frac{\pi }{2} + k\pi (k \in \mathbb{Z})\]
cos x = -1 \[ \Leftrightarrow x = \pi + k2\pi (k \in \mathbb{Z})\]
cos x = 1 \[ \Leftrightarrow x = k2\pi (k \in \mathbb{Z})\]
3. Hàm số tan x
Định nghĩa: Hàm số tan là hàm số được xác định bởi công thức:
y = \[\frac{{\sin x}}{{\cos x}}(\cos x \ne 0)\]
Kí hiệu y = tanx
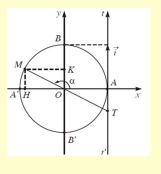
Tính chất:
Tập xác định \[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\].
Tập giá trị: \[\mathbb{R}\] .
Hàm số tuần hoàn với chu kì \[\pi \] , có nghĩa tan( x + \[k\pi \]) = tan x với k\[ \in \]\[\mathbb{Z}\].
Hàm số đồng biến trên mỗi khoảng \[\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\]
y = tan x là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng g và nhận mỗi đường thẳng x = \[\frac{\pi }{2} + k\pi \], k\[ \in \]\[\mathbb{Z}\] làm đường tiệm cận (Hình 3).
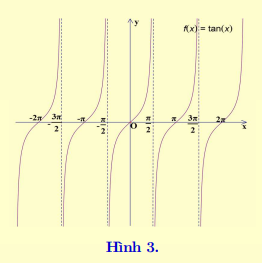
Một số giá trị đặc biệt
tan x = 0 \[ \Leftrightarrow x = k\pi (k \in \mathbb{Z})\]
tan x = 1 \[ \Leftrightarrow x = \frac{\pi }{4} + k\pi (k \in \mathbb{Z})\]
tan x = - 1 \[ \Leftrightarrow x = - \frac{\pi }{4} + k\pi (k \in \mathbb{Z})\]
4. Hàm số cot x
Định nghĩa: Hàm số cot là hàm số được xác định bởi công thức:
y = \[\frac{{\cos x}}{{\sin x}}(\sin x \ne 0)\]
Kí hiệu y = cotx
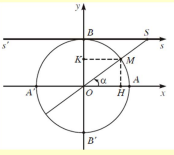
Tính chất:
Tập xác định \[\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\].
Tập giá trị: \[\mathbb{R}\] .
Hàm số tuần hoàn với chu kì \[\pi \] , có nghĩa cot ( x + \[k\pi \]) = cot x với k\[ \in \]\[\mathbb{Z}\].
Hàm số nghịch biến trên mỗi khoảng \[\left( {k\pi ;\pi + k\pi } \right)\]
y = tan x là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng g và nhận mỗi đường thẳng x = \[k\pi \], k\[ \in \]\[\mathbb{Z}\] làm đường tiệm cận (Hình 4).
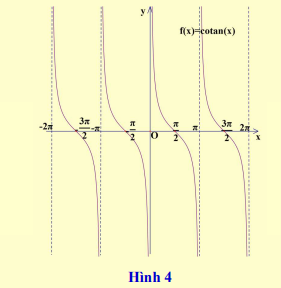
Một số giá trị đặc biệt
cot x = 0 \[ \Leftrightarrow x = \frac{\pi }{2} + k\pi (k \in \mathbb{Z})\]
cot x = 1 \[ \Leftrightarrow x = \frac{\pi }{4} + k\pi (k \in \mathbb{Z})\]
cot x = - 1 \[ \Leftrightarrow x = - \frac{\pi }{4} + k\pi (k \in \mathbb{Z})\]
Phân dạng bài tập
Dạng 1. Tìm tập xác định
Ghi nhớ
y = \[\frac{{f(x)}}{{g(x)}}\]xác định \[ \Leftrightarrow g(x) \ne 0\]
\[y = \sqrt[{2n}]{{f(x)}},n \in \mathbb{N}*\] xác định \[ \Leftrightarrow f(x) \ge 0\]
\[y = \sin [u(x){\rm{]}}\] xác định \[ \Leftrightarrow u(x)\] xác định
\[y = cos[u(x){\rm{]}}\] xác định \[ \Leftrightarrow u(x)\] xác định
\[y = \tan [u(x){\rm{]}}\] xác định \[ \Leftrightarrow u(x)\] xác định và \[u(x) \ne \frac{\pi }{2}{\rm{ + k}}\pi {\rm{,k}} \in \mathbb{Z}\]
\[y = \cot [u(x){\rm{]}}\] xác định \[ \Leftrightarrow u(x)\] xác định và \[u(x) \ne {\rm{k}}\pi {\rm{,k}} \in \mathbb{Z}\]
Bài tập minh họa:
Câu 1: Tìm tập xác định của hàm số y = tan \[\left( {x - \frac{\pi }{6}} \right)\]
Lời giải
Điều kiện: cos \[\left( {x - \frac{\pi }{6}} \right) \ne 0 \Leftrightarrow x - \frac{\pi }{6} \ne \frac{\pi }{2} + k\pi \Leftrightarrow x \ne \frac{{2\pi }}{3} + k\pi \]
TXĐ : \[D = \mathbb{R}\backslash \left\{ {\frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}} \right\}\]
Câu 2: Tìm tập xác định của hàm số y = cot2 \[\left( {\frac{{2\pi }}{3} - 3x} \right)\]
Lời giải
Điều kiện: sin \[\left( {\frac{{2\pi }}{3} - 3x} \right) \ne 0 \Leftrightarrow \frac{{2\pi }}{3} - 3x \ne k\pi \Leftrightarrow \frac{{2\pi }}{9} - k\frac{\pi }{3}\]
TXĐ : \[D = \mathbb{R}\backslash \left\{ {\frac{{2\pi }}{9} + k\frac{\pi }{3},k \in \mathbb{Z}} \right\}\]
Câu 3: Tìm tập xác định của hàm số y = \[\frac{{\tan 2x}}{{\sin x + 1}} + \cot \left( {3x + \frac{\pi }{6}} \right)\]
Lời giải
Điều kiện \[\left\{ {\begin{array}{*{20}{c}}{\sin x \ne - 1}\\{\sin \left( {3x + \frac{\pi }{6}} \right) \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne - \frac{\pi }{2} + k2\pi }\\{x \ne - \frac{\pi }{{18}} + \frac{{k\pi }}{3}}\end{array}} \right.} \right.\]
TXĐ : \[D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{2} + k2\pi , - \frac{\pi }{{18}} + \frac{{k\pi }}{3},k \in \mathbb{Z}} \right\}\]
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack57. All Rights Reserved.
